Algebra homomorphism
Encyclopedia
A homomorphism between two algebras, A and B, over a field
(or ring
) K, is a map
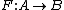such that for all k in K and x,y in A,
If F is bijective then F is said to be an isomorphism between A and B.
A common abbreviation for "homomorphism between algebras" is "algebra homomorphism" or "algebra map". It is easy to see that every algebra homomorphism is a homomorphism of K-modules.
is said to be unital if it maps the unity of A to the unity of B. Often the words "algebra homomorphism" are actually used in the meaning of "unital algebra homomorphism", so non-unital algebra homomorphisms are excluded.
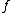in A to 
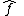in B by the rule 
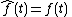. A routine check shows that the mapping 
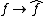is a homomorphism of the algebras A and B. This homomorphism is an isomorphism if and only if K is an infinite field.
Proof. If K is a finite field then let
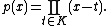
p is a nonzero polynomial in K[x], however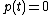
for all t in K, so 
is the zero function and our homomorphism is not an isomorphism (and, actually, the algebras are not isomorphic, since the algebra of polynomials is infinite while that of polynomial functions is finite).
If K is infinite then choose a polynomial f such that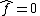
. We want to show this implies that 
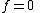. Let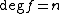 
and let 
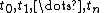be n + 1 distinct elements of K. Then 
for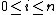 
and by Lagrange interpolation we have 
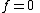. Hence the mapping 
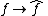is injective. Since this mapping is clearly surjective, it is bijective and thus an algebra isomorphism of A and B.
If A is a subalgebra
of B, then for every invertible b in B the function which takes every a in A to b−1 a b is an algebra homomorphism (in case
, this is called an inner automorphism of B). If A is also simple and B is a central simple algebra
, then every homomorphism from A to B is given in this way by some b in B; this is the Skolem-Noether theorem.
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
(or ring
Algebra (ring theory)
In mathematics, specifically in ring theory, an algebra over a commutative ring is a generalization of the concept of an algebra over a field, where the base field K is replaced by a commutative ring R....
) K, is a map
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
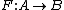such that for all k in K and x,y in A,- F(kx) = kF(x)
- F(x + y) = F(x) + F(y)
- F(xy) = F(x)F(y)
If F is bijective then F is said to be an isomorphism between A and B.
A common abbreviation for "homomorphism between algebras" is "algebra homomorphism" or "algebra map". It is easy to see that every algebra homomorphism is a homomorphism of K-modules.
Unital algebra homomorphisms
If A and B are two unital algebras, then an algebra homomorphism is said to be unital if it maps the unity of A to the unity of B. Often the words "algebra homomorphism" are actually used in the meaning of "unital algebra homomorphism", so non-unital algebra homomorphisms are excluded.Examples
Let A = K[x] be the set of all polynomials over a field K and B be the set of all polynomial functions over K. Both A and B are algebras over K given by the standard multiplication and addition of polynomials and functions, respectively. We can map each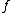 in A to 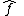in B by the rule 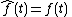. A routine check shows that the mapping 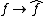is a homomorphism of the algebras A and B. This homomorphism is an isomorphism if and only if K is an infinite field.Proof. If K is a finite field then let
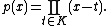
p is a nonzero polynomial in K[x], however
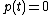for all t in K, so is the zero function and our homomorphism is not an isomorphism (and, actually, the algebras are not isomorphic, since the algebra of polynomials is infinite while that of polynomial functions is finite).If K is infinite then choose a polynomial f such that
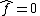. We want to show this implies tha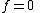t . Let 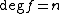and let 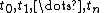be n + 1 distinct elements of K. Then for 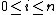and by Lagrange interpolation we have 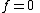. Hence the mapping 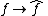is injective. Since this mapping is clearly surjective, it is bijective and thus an algebra isomorphism of A and B.If A is a subalgebra
Subalgebra
In mathematics, the word "algebra", when referring to a structure, often means a vector space or module equipped with an additional bilinear operation. Algebras in universal algebra are far more general: they are a common generalisation of all algebraic structures...
of B, then for every invertible b in B the function which takes every a in A to b−1 a b is an algebra homomorphism (in case
, this is called an inner automorphism of B). If A is also simple and B is a central simple algebraCentral simple algebra
In ring theory and related areas of mathematics a central simple algebra over a field K is a finite-dimensional associative algebra A, which is simple, and for which the center is exactly K...
, then every homomorphism from A to B is given in this way by some b in B; this is the Skolem-Noether theorem.