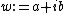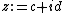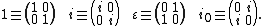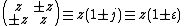Tessarine
Encyclopedia
| × | 1 | i | j | k |
|---|---|---|---|---|
| 1 | 1 | i | j | k |
| i | i | −1 | k | −j |
| j | j | k | +1 | i |
| k | k | −j | i | −1 |
In mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a tessarine is a hypercomplex number
Hypercomplex number
In mathematics, a hypercomplex number is a traditional term for an element of an algebra over a field where the field is the real numbers or the complex numbers. In the nineteenth century number systems called quaternions, tessarines, coquaternions, biquaternions, and octonions became established...
of the form
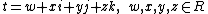
where
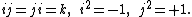
The tessarines are best known for their subalgebra of real tessarines
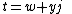,also called split-complex number
Split-complex number
In abstract algebra, the split-complex numbers are a two-dimensional commutative algebra over the real numbers different from the complex numbers. Every split-complex number has the formwhere x and y are real numbers...
s, which express the parametrization of the unit hyperbola
Unit hyperbola
In geometry, the unit hyperbola is the set of points in the Cartesian plane that satisfies x^2 - y^2 = 1 . In the study of indefinite orthogonal groups, the unit hyperbola forms the basis for an alternative radial lengthWhereas the unit circle surrounds its center, the unit hyperbola requires the...
.
James Cockle introduced the tessarines in 1848 in a series of articles in Philosophical Magazine
Philosophical Magazine
The Philosophical Magazine is one of the oldest scientific journals published in English. Initiated by Alexander Tilloch in 1798, in 1822 Richard Taylor became joint editor and it has been published continuously by Taylor & Francis ever since; it was the journal of choice for such luminaries as...
.
Cockle used tessarines to isolate the hyperbolic cosine series and the hyperbolic sine series in the exponential series.
He also showed how zero divisor
Zero divisor
In abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
s arise in tessarines, inspiring him to use the term "impossibles."
In 1892 Corrado Segre
Corrado Segre
Corrado Segre was an Italian mathematician who is remembered today as a major contributor to the early development of algebraic geometry....
introduced bicomplex numbers in Mathematische Annalen
Mathematische Annalen
Mathematische Annalen is a German mathematical research journal founded in 1868 by Alfred Clebsch and Carl Neumann...
, which form an algebra equivalent to the tessarines (see section below). As commutative hypercomplex numbers, the tessarine algebra has been advocated by Clyde M. Davenport (1991, 2008) (exchange j and −k in his multiplication table). Davenport has noted the isomorphism with the direct sum of the complex number plane with itself. Tessarines have also been applied in digital signal processing
Digital signal processing
Digital signal processing is concerned with the representation of discrete time signals by a sequence of numbers or symbols and the processing of these signals. Digital signal processing and analog signal processing are subfields of signal processing...
(see Pei (2004) and Alfsmann (2006,7). In 2009 mathematicians in Vermont
Vermont
Vermont is a state in the New England region of the northeastern United States of America. The state ranks 43rd in land area, , and 45th in total area. Its population according to the 2010 census, 630,337, is the second smallest in the country, larger only than Wyoming. It is the only New England...
proved a fundamental theorem of tessarine algebra: a polynomial of degree n with tessarine coefficients has n2 roots, counting multiplicity.
Linear representation
For tessarine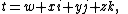
note that 
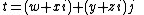since ij = k .The mapping
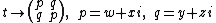
is a linear representation of the algebra of tessarines as a subalgebra of 2 x 2 complex matrices.
For instance, ik = i(ij) = (ii)j = −j in the linear representation is
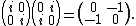
Note that unlike most matrix algebras, this is a commutative algebra.
Isomorphisms to other number systems
In general the tessarines form an algebraAlgebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
of dimension two over the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s with basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
{1, j }
Bicomplex number
Corrado SegreCorrado Segre
Corrado Segre was an Italian mathematician who is remembered today as a major contributor to the early development of algebraic geometry....
read W. R. Hamilton's Lectures on Quaternions (1853) and the works of William Kingdon Clifford
William Kingdon Clifford
William Kingdon Clifford FRS was an English mathematician and philosopher. Building on the work of Hermann Grassmann, he introduced what is now termed geometric algebra, a special case of the Clifford algebra named in his honour, with interesting applications in contemporary mathematical physics...
. Segre used some of Hamilton's notation to develop his system of bicomplex numbers: Let h and i be square roots of −1 that commute with each other. Then, presuming associativity
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
of multiplication, the product hi must have +1 for its square. The algebra constructed on the basis {1, h, i, hi} is then nearly the same as James Cockle's tessarines. Segre noted that elements
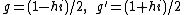are idempotents.When bicomplex numbers are considered to have basis {1, h, i, −hi} then there is no difference between them and tessarines. Looking at the linear representation of these isomorphic algebras shows agreement in the fourth dimension when the negative sign is used; just consider the sample product given above under linear representation.
The University of Kansas
University of Kansas
The University of Kansas is a public research university and the largest university in the state of Kansas. KU campuses are located in Lawrence, Wichita, Overland Park, and Kansas City, Kansas with the main campus being located in Lawrence on Mount Oread, the highest point in Lawrence. The...
has contributed to the development of bicomplex analysis. In 1953, a Ph.D. student James D. Riley had his thesis "Contributions to the theory of functions of a bicomplex variable" published in the Tohoku Mathematical Journal
Tohoku Mathematical Journal
The Tohoku Mathematical Journal is a mathematical research journal published by Tohoku University in Japan. It was founded in August 1911 by Tsuruichi Hayashi....
(2nd Ser., 5:132–165). Then, in 1991, emeritus
Emeritus
Emeritus is a post-positive adjective that is used to designate a retired professor, bishop, or other professional or as a title. The female equivalent emerita is also sometimes used.-History:...
professor G. Baley Price published his book on bicomplex numbers, multicomplex numbers, and their function theory. Professor Price also gives some history of the subject in the preface to his book. Another book developing bicomplex numbers and their applications is by Catoni, Bocaletti, Cannata, Nichelatti & Zampetti (2008).
Direct sum C + C
The direct sum of the complex field with itself is denoted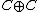
. The product of two elements 
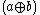and 
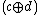is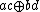 
in this direct sum algebra.Proposition: The algebra of tessarines is isomorphic to
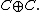
proof: Every tessarine has an expression
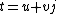where u and v are complex numbers. Now if 
is another tessarine, their product is
The isomorphism mapping from tessarines to
is given by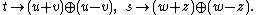
In
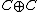, the product of these images, according to the algebra-product of 
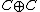indicated above, is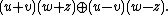
This element is also the image of ts under the mapping into
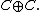
Thus the products agree, the mapping is a homomorphism; and since it is bijective, it is an isomorphism.
Conic quaternion / octonion / sedenion, bicomplex number
When w and z are both complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s
(a, b, c, d real) then t algebra is isomorphic to conic quaternions
, to bases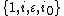 
, in the following identification:
They are also isomorphic to "bicomplex numbers" (from multicomplex numbers) to bases
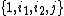if one identifies: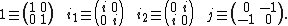
Note that j in bicomplex numbers is identified with the opposite sign as j from above.
When w and z are both quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s (to bases
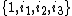), then t algebra is isomorphic to conic octonions; allowing octonionOctonion
In mathematics, the octonions are a normed division algebra over the real numbers, usually represented by the capital letter O, using boldface O or blackboard bold \mathbb O. There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H...
s for w and z (to bases
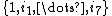) the resulting algebra is identical to conic sedenions.Quotient rings of polynomials
A modern approach to tessarines uses the polynomial ringPolynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
R[X,Y] in two indeterminates X and Y. Consider these three second degree polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s
Let A be the idealIdeal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
generated by them. Then the quotient ring
Quotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
R[X,Y]/A is isomorphic to the ring of tessarines. In this quotient ring approach, individual tessarines correspond to coset
Coset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
s with respect to the ideal A. Note that
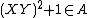can be proven using computations with cosets.Now consider the alternative ideal B generated by
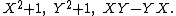
In this case one can prove
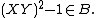The ring isomorphism 
involves a change of basisChange of basis
In linear algebra, change of basis refers to the conversion of vectors and linear transformations between matrix representations which have different bases.-Expression of a basis:...
exchanging
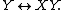
The approach to tessarines by James Cockle resembles the use of ideal A, while Corrado Segre's bicomplex numbers correspond to the use of ideal B.
Alternatively, suppose the field C of ordinary complex numbers is presumed given, and C[X] is the ring of polynomials in X with complex coefficients. Then the quotient
is another presentation of bicomplex numbers.Algebraic properties
Tessarines with w and z complex numbers form a commutative and associative quaternionic ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
(whereas quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s are not commutative). They allow for powers, roots, and logarithms of
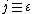, which is a non-real root of 1 (see conic quaternions for examples and references). They do not form a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
because the idempotents
have determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
/ modulus
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
0 and therefore cannot be inverted multiplicatively. In addition, the arithmetic contains zero divisor
Zero divisor
In abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
s
-
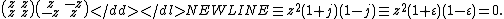
In contrast, the quaternionQuaternionIn mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s form a skew field without zero-divisors, and can also be represented in 2×2 matrix form.
Polynomial roots
Write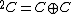
and represent elements of it by ordered pairs (u,v) of complex numbers. Since the algebra of tessarines T is isomorphic to 
, the rings of polynomials T[X] and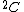 
[X] are also isomorphic, however polynomials in the latter algebra split: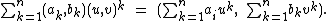
In consequence, when a polynomial equation
in this algebra is set, it reduces to two polynomial equations on C. If the degree is n, then there are n roots for each equation: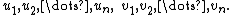 
Any ordered pair
from this set of roots will satisfy the original equation in 2C[X], so it has n2 roots.
Due to the isomorphism with T[X], there is a correspondence of polynomials and a correspondence of their roots. Hence the tessarine polynomials of degree n also have n2 roots, counting multiplicity of rootsMultiplicity (mathematics)In mathematics, the multiplicity of a member of a multiset is the number of times it appears in the multiset. For example, the number of times a given polynomial equation has a root at a given point....
.