
Tate conjecture
Encyclopedia
In mathematics
, the Tate conjecture is a 1963 conjecture
of John Tate
linking algebraic geometry
, and more specifically the identification of algebraic cycle
s, with Galois module
s coming from étale cohomology
. It is unsolved in the general case, , and, like the Hodge conjecture
to which it is related at the level of some important analogies, it is generally taken to be one of the major problems in the field.
Tate's original statement runs as follows. Let V be a smooth algebraic variety
over a field
k, which is finitely-generated over its prime field. Let G be the absolute Galois group
of k. Fix a prime number
l. Write H*(V) for the l-adic cohomology (coefficients in the l-adic integers, scalars then extended to the l-adic numbers) of the base extension of V to the given algebraic closure
of k; these groups are G-modules. Consider
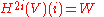
for the i-fold Tate twist
of the cohomology group in degree 2i, for i = 1, 2, ..., d where d is the dimension
of V. Under the Galois action, the image of G is a compact subgroup
of GL(V), which is an l-adic Lie group
. It follows by the l-adic version of Cartan's theorem
that as a closed subgroup it is also a Lie subgroup
, with corresponding Lie algebra
. Tate's conjecture concerns the subspace W ′ of W invariant under this Lie algebra (that is, on which the infinitesimal transformation
s of the Lie algebra representation act as 0). There is another characterization used for W ′, namely that it consists of vectors w in W that have an open stabilizer in G, or again have a finite orbit.
Then the Tate conjecture states that W ′ is also the subspace of W generated by the cohomology classes of algebraic cycle
s of codimension
i on V.
An immediate application, also given by Tate, takes V as the cartesian product
of two abelian varieties, and deduces a conjecture relating the morphisms from one abelian variety to another to intertwining maps for the Tate module
s. This is also known as the Tate conjecture, and several results have been proved towards it.
The same paper also contains related conjectures on L-function
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Tate conjecture is a 1963 conjecture
Conjecture
A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...
of John Tate
John Tate
John Torrence Tate Jr. is an American mathematician, distinguished for many fundamental contributions in algebraic number theory, arithmetic geometry and related areas in algebraic geometry.-Biography:...
linking algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, and more specifically the identification of algebraic cycle
Algebraic cycle
In mathematics, an algebraic cycle on an algebraic variety V is, roughly speaking, a homology class on V that is represented by a linear combination of subvarieties of V. Therefore the algebraic cycles on V are the part of the algebraic topology of V that is directly accessible in algebraic geometry...
s, with Galois module
Galois module
In mathematics, a Galois module is a G-module where G is the Galois group of some extension of fields. The term Galois representation is frequently used when the G-module is a vector space over a field or a free module over a ring, but can also be used as a synonym for G-module...
s coming from étale cohomology
Étale cohomology
In mathematics, the étale cohomology groups of an algebraic variety or scheme are algebraic analogues of the usual cohomology groups with finite coefficients of a topological space, introduced by Grothendieck in order to prove the Weil conjectures...
. It is unsolved in the general case, , and, like the Hodge conjecture
Hodge conjecture
The Hodge conjecture is a major unsolved problem in algebraic geometry which relates the algebraic topology of a non-singular complex algebraic variety and the subvarieties of that variety. More specifically, the conjecture says that certain de Rham cohomology classes are algebraic, that is, they...
to which it is related at the level of some important analogies, it is generally taken to be one of the major problems in the field.
Tate's original statement runs as follows. Let V be a smooth algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
k, which is finitely-generated over its prime field. Let G be the absolute Galois group
Absolute Galois group
In mathematics, the absolute Galois group GK of a field K is the Galois group of Ksep over K, where Ksep is a separable closure of K. Alternatively it is the group of all automorphisms of the algebraic closure of K that fix K. The absolute Galois group is unique up to isomorphism...
of k. Fix a prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
l. Write H*(V) for the l-adic cohomology (coefficients in the l-adic integers, scalars then extended to the l-adic numbers) of the base extension of V to the given algebraic closure
Algebraic closure
In mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
of k; these groups are G-modules. Consider
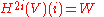
for the i-fold Tate twist
Tate twist
In number theory and algebraic geometry, the Tate twist, named after John Tate, is an operation on Galois modules.For example, if K is a field, GK is its absolute Galois group, and ρ : GK → AutK is a representation of GK on a finite-dimensional vector space V over the field Qp of p-adic numbers,...
of the cohomology group in degree 2i, for i = 1, 2, ..., d where d is the dimension
Dimension of an algebraic variety
In mathematics, the dimension of an algebraic variety V in algebraic geometry is defined, informally speaking, as the number of independent rational functions that exist on V.For example, an algebraic curve has by definition dimension 1...
of V. Under the Galois action, the image of G is a compact subgroup
Compact group
In mathematics, a compact group is a topological group whose topology is compact. Compact groups are a natural generalisation of finite groups with the discrete topology and have properties that carry over in significant fashion...
of GL(V), which is an l-adic Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
. It follows by the l-adic version of Cartan's theorem
Cartan's theorem
In mathematics, three results in Lie group theory are called Cartan's theorem, named after Élie Cartan:See also Cartan's theorems A and B, results of Henri Cartan, and Cartan's lemma for various other results attributed to Élie and Henri Cartan....
that as a closed subgroup it is also a Lie subgroup
Lie subgroup
In mathematics, a Lie subgroup H of a Lie group G is a Lie group that is a subset of G and such that the inclusion map from H to G is an injective immersion and group homomorphism. According to Cartan's theorem, a closed subgroup of G admits a unique smooth structure which makes it an embedded Lie...
, with corresponding Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
. Tate's conjecture concerns the subspace W ′ of W invariant under this Lie algebra (that is, on which the infinitesimal transformation
Infinitesimal transformation
In mathematics, an infinitesimal transformation is a limiting form of small transformation. For example one may talk about an infinitesimal rotation of a rigid body, in three-dimensional space. This is conventionally represented by a 3×3 skew-symmetric matrix A...
s of the Lie algebra representation act as 0). There is another characterization used for W ′, namely that it consists of vectors w in W that have an open stabilizer in G, or again have a finite orbit.
Then the Tate conjecture states that W ′ is also the subspace of W generated by the cohomology classes of algebraic cycle
Algebraic cycle
In mathematics, an algebraic cycle on an algebraic variety V is, roughly speaking, a homology class on V that is represented by a linear combination of subvarieties of V. Therefore the algebraic cycles on V are the part of the algebraic topology of V that is directly accessible in algebraic geometry...
s of codimension
Codimension
In mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, and also to submanifolds in manifolds, and suitable subsets of algebraic varieties.The dual concept is relative dimension.-Definition:...
i on V.
An immediate application, also given by Tate, takes V as the cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of two abelian varieties, and deduces a conjecture relating the morphisms from one abelian variety to another to intertwining maps for the Tate module
Tate module
In mathematics, a Tate module of an abelian group, named for John Tate, is a module constructed from an abelian group A. Often, this construction is made in the following situation: G is a commutative group scheme over a field K, Ks is the separable closure of K, and A = G...
s. This is also known as the Tate conjecture, and several results have been proved towards it.
The same paper also contains related conjectures on L-function
L-function
The theory of L-functions has become a very substantial, and still largely conjectural, part of contemporary analytic number theory. In it, broad generalisations of the Riemann zeta function and the L-series for a Dirichlet character are constructed, and their general properties, in most cases...
s.

