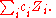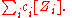Hodge conjecture
Encyclopedia
The Hodge conjecture is a major unsolved problem in algebraic geometry
which relates the algebraic topology
of a non-singular complex
algebraic variety
and the subvarieties of that variety. More specifically, the conjecture says that certain de Rham cohomology
classes are algebraic, that is, they are sums of Poincaré duals
of the homology classes of subvarieties. The Hodge conjecture is one of the Clay Mathematics Institute
's Millennium Prize Problems
, with a prize of $1,000,000 for whoever can prove or disprove the Hodge conjecture using "some argument". It was formulated by the Scottish mathematician William Vallance Douglas Hodge as a result of a work in between 1930 and 1940 to enrich the description of De Rham cohomology to include extra structure which is present in the case of complex algebraic varieties.
complex manifold
of complex dimension n. Then X is an orientable smooth manifold of real dimension 2n, so its cohomology groups lie in degrees zero through 2n. X is a Kähler manifold
, so that there is a decomposition on its cohomology with complex coefficients:

where is the subgroup of cohomology classes which are represented by harmonic forms of type (p, q). That is, these are the cohomology classes represented by differential form
is the subgroup of cohomology classes which are represented by harmonic forms of type (p, q). That is, these are the cohomology classes represented by differential form
s which, in some choice of local coordinates , can be written as a harmonic function
, can be written as a harmonic function
times . (See Hodge theory
. (See Hodge theory
for more details.) Taking wedge products of these harmonic representatives corresponds to the cup product
in cohomology, so the cup product is compatible with the Hodge decomposition:
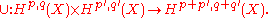
Since X is a compact oriented manifold, X has a fundamental class
.
Let Z be a complex submanifold of X of dimension k, and let i : Z → X be the inclusion map. Choose a differential form of type (p, q). We can integrate
of type (p, q). We can integrate  over Z:
over Z:

To evaluate this integral, choose a point of Z and call it 0. Around 0, we can choose local coordinates on X such that Z is just
on X such that Z is just  . If p > k, then
. If p > k, then  must contain some
must contain some  where
where  pulls back to zero on Z. The same is true if q > k. Consequently, this integral is zero if (p, q) ≠ (k, k).
pulls back to zero on Z. The same is true if q > k. Consequently, this integral is zero if (p, q) ≠ (k, k).
More abstractly, the integral can be written as the cap product
of the homology class of Z and the cohomology class represented by . By Poincaré duality, the homology class of Z is dual to a cohomology class which we will call [Z], and the cap product can be computed by taking the cup product of [Z] and
. By Poincaré duality, the homology class of Z is dual to a cohomology class which we will call [Z], and the cap product can be computed by taking the cup product of [Z] and  and capping with the fundamental class of X. Because [Z] is a cohomology class, it has a Hodge decomposition. By the computation we did above, if we cup this class with any class of type (p, q) ≠ (k, k), then we get zero. Because
and capping with the fundamental class of X. Because [Z] is a cohomology class, it has a Hodge decomposition. By the computation we did above, if we cup this class with any class of type (p, q) ≠ (k, k), then we get zero. Because 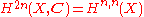 , we conclude that [Z] must lie in
, we conclude that [Z] must lie in 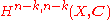 . Loosely speaking, the Hodge conjecture asks:
. Loosely speaking, the Hodge conjecture asks:
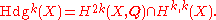
We call this the group of Hodge classes of degree 2k on X.
The modern statement of the Hodge conjecture is:
A projective complex manifold is a complex manifold which can be embedded in complex projective space
. Because projective space carries a Kähler metric, the Fubini–Study metric, such a manifold is always a Kähler manifold. By Chow's theorem, a projective complex manifold is also a smooth projective algebraic variety, that is, it is the zero set of a collection of homogenous polynomials.
on X is a formal combination of subvarieties of X, that is, it is something of the form:
The coefficients are usually taken to be integral or rational. We define the cohomology class of an algebraic cycle to be the sum of the cohomology classes of its components. This is an example of the cycle class map of de Rham cohomology, see Weil cohomology. For example, the cohomology class of the above cycle would be:
Such a cohomology class is called algebraic. With this notation, the Hodge conjecture becomes:
A very quick proof can be given using sheaf cohomology
and the exponential exact sequence. (The cohomology class of a divisor turns out to equal to its first Chern class
.) Lefschetz's original proof proceeded by normal functions, which were introduced by Henri Poincaré
. However, Griffiths transversality theorem shows that this approach cannot prove the Hodge conjecture for higher codimensional subvarieties.
By the Hard Lefschetz theorem, one can prove:
Combining the above two theorems implies that Hodge conjecture is true for Hodge classes of degree 2n − 2. This proves the Hodge conjecture when X has dimension at most three.
The Lefschetz theorem on (1,1)-classes also implies that if all Hodge classes are generated by the Hodge classes of divisors, then the Hodge conjecture is true:
, the algebra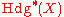 is generated in degree one, so the Hodge conjecture holds. In particular, the Hodge conjecture holds for sufficiently general abelian varieties, for products of elliptic curves, and for simple abelian varieties. However, constructed an example of an abelian variety where
is generated in degree one, so the Hodge conjecture holds. In particular, the Hodge conjecture holds for sufficiently general abelian varieties, for products of elliptic curves, and for simple abelian varieties. However, constructed an example of an abelian variety where  is not generated by products of divisor classes. generalized this example by showing that whenever the variety has complex multiplication
is not generated by products of divisor classes. generalized this example by showing that whenever the variety has complex multiplication
by an imaginary quadratic field, then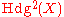 is not generated by products of divisor classes. proved that in dimension less than 5, either
is not generated by products of divisor classes. proved that in dimension less than 5, either 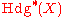 is generated in degree one, or the variety has complex multiplication by an imaginary quadratic field. In the latter case, the Hodge conjecture is only known in special cases.
is generated in degree one, or the variety has complex multiplication by an imaginary quadratic field. In the latter case, the Hodge conjecture is only known in special cases.
This is now known to be false. The first counterexample was constructed by . Using K-theory
, they constructed an example of a torsion Hodge class, that is, a Hodge class such that for some positive integer n,
such that for some positive integer n,  . Such a cohomology class cannot be the class of a cycle. reinterpreted their result in the framework of cobordism
. Such a cohomology class cannot be the class of a cycle. reinterpreted their result in the framework of cobordism
and found many examples of torsion classes.
The simplest adjustment of the integral Hodge conjecture is:
This is also false. found an example of a Hodge class which is not algebraic, but which has an integral multiple which is algebraic.
which is not algebraic, but which has an integral multiple which is algebraic.
This is too optimistic, because there are not enough subvarieties to make this work. A possible substitute is to ask instead one of the two following questions:
proved that the Chern classes of coherent sheaves give strictly more Hodge classes than the Chern classes of vector bundles and that the Chern classes of coherent sheaves are insufficient to generate all the Hodge classes. Consequently, the only known formulations of the Hodge conjecture for Kähler varieties are false.
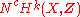 satisfies
satisfies
Hodge's original statement was:
observed that this cannot be true, even with rational coefficients, because the right-hand side is not always a Hodge structure. His corrected form of the Hodge conjecture is:
This version is open.
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
which relates the algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
of a non-singular complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
and the subvarieties of that variety. More specifically, the conjecture says that certain de Rham cohomology
De Rham cohomology
In mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
classes are algebraic, that is, they are sums of Poincaré duals
Poincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
of the homology classes of subvarieties. The Hodge conjecture is one of the Clay Mathematics Institute
Clay Mathematics Institute
The Clay Mathematics Institute is a private, non-profit foundation, based in Cambridge, Massachusetts. The Institute is dedicated to increasing and disseminating mathematical knowledge. It gives out various awards and sponsorships to promising mathematicians. The institute was founded in 1998...
's Millennium Prize Problems
Millennium Prize Problems
The Millennium Prize Problems are seven problems in mathematics that were stated by the Clay Mathematics Institute in 2000. As of September 2011, six of the problems remain unsolved. A correct solution to any of the problems results in a US$1,000,000 prize being awarded by the institute...
, with a prize of $1,000,000 for whoever can prove or disprove the Hodge conjecture using "some argument". It was formulated by the Scottish mathematician William Vallance Douglas Hodge as a result of a work in between 1930 and 1940 to enrich the description of De Rham cohomology to include extra structure which is present in the case of complex algebraic varieties.
Motivation
Let X be a compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
of complex dimension n. Then X is an orientable smooth manifold of real dimension 2n, so its cohomology groups lie in degrees zero through 2n. X is a Kähler manifold
Kähler manifold
In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
, so that there is a decomposition on its cohomology with complex coefficients:

where
 is the subgroup of cohomology classes which are represented by harmonic forms of type (p, q). That is, these are the cohomology classes represented by differential form
is the subgroup of cohomology classes which are represented by harmonic forms of type (p, q). That is, these are the cohomology classes represented by differential formDifferential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s which, in some choice of local coordinates
 , can be written as a harmonic function
, can be written as a harmonic functionHarmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
times
 . (See Hodge theory
. (See Hodge theoryHodge theory
In mathematics, Hodge theory, named after W. V. D. Hodge, is one aspect of the study of the algebraic topology of a smooth manifold M. More specifically, it works out the consequences for the cohomology groups of M, with real coefficients, of the partial differential equation theory of generalised...
for more details.) Taking wedge products of these harmonic representatives corresponds to the cup product
Cup product
In mathematics, specifically in algebraic topology, the cup product is a method of adjoining two cocycles of degree p and q to form a composite cocycle of degree p + q. This defines an associative graded commutative product operation in cohomology, turning the cohomology of a space X into a...
in cohomology, so the cup product is compatible with the Hodge decomposition:
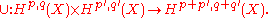
Since X is a compact oriented manifold, X has a fundamental class
Fundamental class
In mathematics, the fundamental class is a homology class [M] associated to an oriented manifold M, which corresponds to "the whole manifold", and pairing with which corresponds to "integrating over the manifold"...
.
Let Z be a complex submanifold of X of dimension k, and let i : Z → X be the inclusion map. Choose a differential form
 of type (p, q). We can integrate
of type (p, q). We can integrate  over Z:
over Z:
To evaluate this integral, choose a point of Z and call it 0. Around 0, we can choose local coordinates
 on X such that Z is just
on X such that Z is just  . If p > k, then
. If p > k, then  must contain some
must contain some  where
where  pulls back to zero on Z. The same is true if q > k. Consequently, this integral is zero if (p, q) ≠ (k, k).
pulls back to zero on Z. The same is true if q > k. Consequently, this integral is zero if (p, q) ≠ (k, k).More abstractly, the integral can be written as the cap product
Cap product
In algebraic topology the cap product is a method of adjoining a chain of degree p with a cochain of degree q, such that q ≤ p, to form a composite chain of degree p − q. It was introduced by Eduard Čech in 1936, and independently by Hassler Whitney in 1938.-Definition:Let X be a topological...
of the homology class of Z and the cohomology class represented by
 . By Poincaré duality, the homology class of Z is dual to a cohomology class which we will call [Z], and the cap product can be computed by taking the cup product of [Z] and
. By Poincaré duality, the homology class of Z is dual to a cohomology class which we will call [Z], and the cap product can be computed by taking the cup product of [Z] and  and capping with the fundamental class of X. Because [Z] is a cohomology class, it has a Hodge decomposition. By the computation we did above, if we cup this class with any class of type (p, q) ≠ (k, k), then we get zero. Because
and capping with the fundamental class of X. Because [Z] is a cohomology class, it has a Hodge decomposition. By the computation we did above, if we cup this class with any class of type (p, q) ≠ (k, k), then we get zero. Because 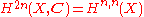 , we conclude that [Z] must lie in
, we conclude that [Z] must lie in 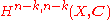 . Loosely speaking, the Hodge conjecture asks:
. Loosely speaking, the Hodge conjecture asks:
- Which cohomology classes in
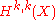 come from complex subvarieties Z?
come from complex subvarieties Z?
Statement of the Hodge conjecture
Let: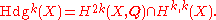
We call this the group of Hodge classes of degree 2k on X.
The modern statement of the Hodge conjecture is:
- Hodge conjecture. Let X be a projective complex manifold. Then every Hodge class on X is a linear combination with rational coefficients of the cohomology classes of complex subvarieties of X.
A projective complex manifold is a complex manifold which can be embedded in complex projective space
Complex projective space
In mathematics, complex projective space is the projective space with respect to the field of complex numbers. By analogy, whereas the points of a real projective space label the lines through the origin of a real Euclidean space, the points of a complex projective space label the complex lines...
. Because projective space carries a Kähler metric, the Fubini–Study metric, such a manifold is always a Kähler manifold. By Chow's theorem, a projective complex manifold is also a smooth projective algebraic variety, that is, it is the zero set of a collection of homogenous polynomials.
Reformulation in terms of algebraic cycles
Another way of phrasing the Hodge conjecture involves the idea of an algebraic cycle. An algebraic cycleAlgebraic cycle
In mathematics, an algebraic cycle on an algebraic variety V is, roughly speaking, a homology class on V that is represented by a linear combination of subvarieties of V. Therefore the algebraic cycles on V are the part of the algebraic topology of V that is directly accessible in algebraic geometry...
on X is a formal combination of subvarieties of X, that is, it is something of the form:
The coefficients are usually taken to be integral or rational. We define the cohomology class of an algebraic cycle to be the sum of the cohomology classes of its components. This is an example of the cycle class map of de Rham cohomology, see Weil cohomology. For example, the cohomology class of the above cycle would be:
Such a cohomology class is called algebraic. With this notation, the Hodge conjecture becomes:
- Let X be a projective complex manifold. Then every Hodge class on X is algebraic.
Low dimension and codimension
The first result on the Hodge conjecture is due to . In fact, it predates the conjecture and provided some of Hodge's motivation.- Theorem (Lefschetz theorem on (1,1)-classesLefschetz theorem on (1,1)-classesIn algebraic geometry, a branch of mathematics, the Lefschetz theorem on -classes, named after Solomon Lefschetz, is a classical statement relating divisors on a compact Kähler manifold to classes in its integral cohomology. It is the only case of the Hodge conjecture which has been proved for all...
) Any element of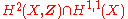 is the cohomology class of a divisorDivisor (algebraic geometry)In algebraic geometry, divisors are a generalization of codimension one subvarieties of algebraic varieties; two different generalizations are in common use, Cartier divisors and Weil divisors...
is the cohomology class of a divisorDivisor (algebraic geometry)In algebraic geometry, divisors are a generalization of codimension one subvarieties of algebraic varieties; two different generalizations are in common use, Cartier divisors and Weil divisors...
on X. In particular, the Hodge conjecture is true for .
.
A very quick proof can be given using sheaf cohomology
Sheaf cohomology
In mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
and the exponential exact sequence. (The cohomology class of a divisor turns out to equal to its first Chern class
Chern class
In mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
.) Lefschetz's original proof proceeded by normal functions, which were introduced by Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
. However, Griffiths transversality theorem shows that this approach cannot prove the Hodge conjecture for higher codimensional subvarieties.
By the Hard Lefschetz theorem, one can prove:
- Theorem. If the Hodge conjecture holds for Hodge classes of degree p, p < n, then the Hodge conjecture holds for Hodge classes of degree 2n − p.
Combining the above two theorems implies that Hodge conjecture is true for Hodge classes of degree 2n − 2. This proves the Hodge conjecture when X has dimension at most three.
The Lefschetz theorem on (1,1)-classes also implies that if all Hodge classes are generated by the Hodge classes of divisors, then the Hodge conjecture is true:
- Corollary. If the algebra
-
- is generated by Hdg1(X), then the Hodge conjecture holds for X.
Abelian varieties
For most abelian varietiesAbelian variety
In mathematics, particularly in algebraic geometry, complex analysis and number theory, an abelian variety is a projective algebraic variety that is also an algebraic group, i.e., has a group law that can be defined by regular functions...
, the algebra
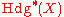 is generated in degree one, so the Hodge conjecture holds. In particular, the Hodge conjecture holds for sufficiently general abelian varieties, for products of elliptic curves, and for simple abelian varieties. However, constructed an example of an abelian variety where
is generated in degree one, so the Hodge conjecture holds. In particular, the Hodge conjecture holds for sufficiently general abelian varieties, for products of elliptic curves, and for simple abelian varieties. However, constructed an example of an abelian variety where  is not generated by products of divisor classes. generalized this example by showing that whenever the variety has complex multiplication
is not generated by products of divisor classes. generalized this example by showing that whenever the variety has complex multiplicationComplex multiplication
In mathematics, complex multiplication is the theory of elliptic curves E that have an endomorphism ring larger than the integers; and also the theory in higher dimensions of abelian varieties A having enough endomorphisms in a certain precise sense In mathematics, complex multiplication is the...
by an imaginary quadratic field, then
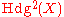 is not generated by products of divisor classes. proved that in dimension less than 5, either
is not generated by products of divisor classes. proved that in dimension less than 5, either 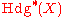 is generated in degree one, or the variety has complex multiplication by an imaginary quadratic field. In the latter case, the Hodge conjecture is only known in special cases.
is generated in degree one, or the variety has complex multiplication by an imaginary quadratic field. In the latter case, the Hodge conjecture is only known in special cases.The integral Hodge conjecture
Hodge's original conjecture was:- Integral Hodge conjecture. Let X be a projective complex manifold. Then every cohomology class in
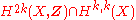 is the cohomology class of an algebraic cycle with integral coefficients on X.
is the cohomology class of an algebraic cycle with integral coefficients on X.
This is now known to be false. The first counterexample was constructed by . Using K-theory
K-theory
In mathematics, K-theory originated as the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is an extraordinary cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It...
, they constructed an example of a torsion Hodge class, that is, a Hodge class
 such that for some positive integer n,
such that for some positive integer n,  . Such a cohomology class cannot be the class of a cycle. reinterpreted their result in the framework of cobordism
. Such a cohomology class cannot be the class of a cycle. reinterpreted their result in the framework of cobordismCobordism
In mathematics, cobordism is a fundamental equivalence relation on the class of compact manifolds of the same dimension, set up using the concept of the boundary of a manifold. Two manifolds are cobordant if their disjoint union is the boundary of a manifold one dimension higher. The name comes...
and found many examples of torsion classes.
The simplest adjustment of the integral Hodge conjecture is:
- Integral Hodge conjecture modulo torsion. Let X be a projective complex manifold. Then every non-torsion cohomology class in
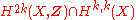 is the cohomology class of an algebraic cycle with integral coefficients on X.
is the cohomology class of an algebraic cycle with integral coefficients on X.
This is also false. found an example of a Hodge class
 which is not algebraic, but which has an integral multiple which is algebraic.
which is not algebraic, but which has an integral multiple which is algebraic.The Hodge conjecture for Kähler varieties
A natural generalization of the Hodge conjecture would ask:- Hodge conjecture for Kähler varieties, naive version. Let X be a complex Kähler manifold. Then every Hodge class on X is a linear combination with rational coefficients of the cohomology classes of complex subvarieties of X.
This is too optimistic, because there are not enough subvarieties to make this work. A possible substitute is to ask instead one of the two following questions:
- Hodge conjecture for Kähler varieties, vector bundle version. Let X be a complex Kähler manifold. Then every Hodge class on X is a linear combination with rational coefficients of Chern classes of vector bundles on X.
- Hodge conjecture for Kähler varieties, coherent sheaf version. Let X be a complex Kähler manifold. Then every Hodge class on X is a linear combination with rational coefficients of Chern classes of coherent sheaves on X.
proved that the Chern classes of coherent sheaves give strictly more Hodge classes than the Chern classes of vector bundles and that the Chern classes of coherent sheaves are insufficient to generate all the Hodge classes. Consequently, the only known formulations of the Hodge conjecture for Kähler varieties are false.
The generalized Hodge conjecture
Hodge made an additional, stronger conjecture than the integral Hodge conjecture. Say that a cohomology class on X is of level c if it is the pushforward of a cohomology class on a c-codimensional subvariety of X. The cohomology classes of level at least c filter the cohomology of X, and it is easy to see that the cth step of the filtration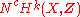 satisfies
satisfies
Hodge's original statement was:
- Generalized Hodge conjecture, Hodge's version.
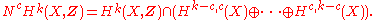
observed that this cannot be true, even with rational coefficients, because the right-hand side is not always a Hodge structure. His corrected form of the Hodge conjecture is:
- Generalized Hodge conjecture.
 is the largest sub-Hodge structure of
is the largest sub-Hodge structure of 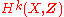 contained in
contained in 
This version is open.
Algebraicity of Hodge loci
The strongest evidence in favor of the Hodge conjecture is the algebraicity result of . Suppose that we vary the complex structure of X over a simply connected base. Then the topological cohomology of X does not change, but the Hodge decomposition does change. It is known that if the Hodge conjecture is true, then the locus of all points on the base where the cohomology of a fiber is a Hodge class is in fact an algebraic subset, that is, it is cut out by polynomial equations. Cattani, Deligne & Kaplan (1995) proved that this is always true, without assuming the Hodge conjecture.External links
- The Clay Math Institute Official Problem Description (pdf)
- Popular lecture on Hodge Conjecture by Dan Freed (University of Texas) (Real Video) (Slides)
- Indranil Biswas; Kapil Paranjape. The Hodge Conjecture for general Prym varieties