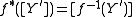Algebraic cycle
Encyclopedia
In mathematics
, an algebraic cycle on an algebraic variety
V is, roughly speaking, a homology class on V that is represented by a linear combination of subvarieties of V. Therefore the algebraic cycles on V are the part of the algebraic topology
of V that is directly accessible in algebraic geometry
. With the formulation of some fundamental conjectures in the 1950s and 1960s, the study of algebraic cycles became one of the main objectives of the algebraic geometry of general varieties.
The nature of the difficulties is quite plain: the existence of algebraic cycles is easy to predict, but the current methods of constructing them are deficient. The major conjectures on algebraic cycles include the Hodge conjecture
and the Tate conjecture
. In the search for a proof of the Weil conjectures
, Alexander Grothendieck
and Enrico Bombieri
formulated what are now known as the standard conjectures of algebraic cycle
theory.
Algebraic cycles have also been shown to be closely connected with algebraic K-theory
.
For the purposes of a well-working intersection theory
, one uses various equivalence relations on algebraic cycles. Particularly important is the so-called rational equivalence. Cycles up to rational equivalence form a graded ring, the Chow ring
, whose multiplication is given by the intersection product. Further fundamental relations include algebraic equivalence, numerical equivalence, and homological equivalence. They have (partly conjectural) applications in the theory of motives
.
X is a formal linear combination V = ∑ ni·Vi of irreducible reduced closed subschemes. A coefficient ni is called multiplicity of Vi in V. Ad hoc, the coefficients are integers, but rational coefficients are also widely used.
Under the correspondence
(V maps to its generic point
(with respect to the Zariski topology
), conversely a point maps to its closure (with the reduced subscheme structure))
an algebraic cycle is thus just a formal linear combination of points of X.
The group of cycles naturally forms a group Z*(X) graded by the dimension of the cycles. The grading by codimension is also useful, then the group is usually written Z*(X).
' be a map of varieties.
If f is flat
of some constant relative dimension (i.e. all fibers have the same dimension), we can define for any subvariety Y' ⊂ X' :
which by assumption has the same codimension as Y′.
Conversely, if f is proper, for Y a subvariety of X the pushforward is defined to be
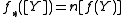
where n is the degree of the extension of function fields
[k(Y) : k(f(Y))] if the restriction of f to Y is finite and 0 otherwise.
By linearity, these definitions extend to homomorphisms of abelian groups
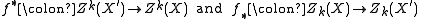
(the latter by virtue of the convention) are homomorphisms of abelian groups. See Chow ring
for a discussion of the functoriality related to the ring structure.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an algebraic cycle on an algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
V is, roughly speaking, a homology class on V that is represented by a linear combination of subvarieties of V. Therefore the algebraic cycles on V are the part of the algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
of V that is directly accessible in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
. With the formulation of some fundamental conjectures in the 1950s and 1960s, the study of algebraic cycles became one of the main objectives of the algebraic geometry of general varieties.
The nature of the difficulties is quite plain: the existence of algebraic cycles is easy to predict, but the current methods of constructing them are deficient. The major conjectures on algebraic cycles include the Hodge conjecture
Hodge conjecture
The Hodge conjecture is a major unsolved problem in algebraic geometry which relates the algebraic topology of a non-singular complex algebraic variety and the subvarieties of that variety. More specifically, the conjecture says that certain de Rham cohomology classes are algebraic, that is, they...
and the Tate conjecture
Tate conjecture
In mathematics, the Tate conjecture is a 1963 conjecture of John Tate linking algebraic geometry, and more specifically the identification of algebraic cycles, with Galois modules coming from étale cohomology...
. In the search for a proof of the Weil conjectures
Weil conjectures
In mathematics, the Weil conjectures were some highly-influential proposals by on the generating functions derived from counting the number of points on algebraic varieties over finite fields....
, Alexander Grothendieck
Alexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
and Enrico Bombieri
Enrico Bombieri
Enrico Bombieri is a mathematician who has been working at the Institute for Advanced Study in Princeton, New Jersey. Bombieri's research in number theory, algebraic geometry, and mathematical analysis have earned him many international prizes --- a Fields Medal in 1974 and the Balzan Prize in 1980...
formulated what are now known as the standard conjectures of algebraic cycle
Standard conjectures on algebraic cycles
In mathematics, the standard conjectures about algebraic cycles is a package of several conjectures describing the relationship of algebraic cycles and Weil cohomology theories. One of the original applications of these conjectures, envisaged by Alexander Grothendieck, was to prove that his...
theory.
Algebraic cycles have also been shown to be closely connected with algebraic K-theory
Algebraic K-theory
In mathematics, algebraic K-theory is an important part of homological algebra concerned with defining and applying a sequenceof functors from rings to abelian groups, for all integers n....
.
For the purposes of a well-working intersection theory
Intersection theory
In mathematics, intersection theory is a branch of algebraic geometry, where subvarieties are intersected on an algebraic variety, and of algebraic topology, where intersections are computed within the cohomology ring. The theory for varieties is older, with roots in Bézout's theorem on curves and...
, one uses various equivalence relations on algebraic cycles. Particularly important is the so-called rational equivalence. Cycles up to rational equivalence form a graded ring, the Chow ring
Chow ring
In algebraic geometry, the Chow ring of an algebraic variety is an algebraic-geometric analogue of the cohomology ring of the variety considered as a topological space: its elements are formed out of actual subvarieties and its multiplicative structure is derived from the intersection of...
, whose multiplication is given by the intersection product. Further fundamental relations include algebraic equivalence, numerical equivalence, and homological equivalence. They have (partly conjectural) applications in the theory of motives
Motive (algebraic geometry)
In algebraic geometry, a motive denotes 'some essential part of an algebraic variety'. To date, pure motives have been defined, while conjectural mixed motives have not. Pure motives are triples , where X is a smooth projective variety, p : X ⊢ X is an idempotent correspondence, and m an integer...
.
Definition
An algebraic cycle of an algebraic variety or schemeScheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
X is a formal linear combination V = ∑ ni·Vi of irreducible reduced closed subschemes. A coefficient ni is called multiplicity of Vi in V. Ad hoc, the coefficients are integers, but rational coefficients are also widely used.
Under the correspondence
- {irreducibleIrreducible componentIn mathematics, the concept of irreducible component is used to make formal the idea that a set such as defined by the equationis the union of the two linesandThe notion of irreducibility is stronger than connectedness.- Definition :...
reduced closed subschemes V ⊂ X} ↭ {points of X}
(V maps to its generic point
Generic point
In mathematics, in the fields general topology and particularly of algebraic geometry, a generic point P of a topological space X is an algebraic way of capturing the notion of a generic property: a generic property is a property of the generic point.- Definition and motivation :A generic point of...
(with respect to the Zariski topology
Zariski topology
In algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...
), conversely a point maps to its closure (with the reduced subscheme structure))
an algebraic cycle is thus just a formal linear combination of points of X.
The group of cycles naturally forms a group Z*(X) graded by the dimension of the cycles. The grading by codimension is also useful, then the group is usually written Z*(X).
Flat pullback and proper pushforward
There is a covariant and a contravariant functoriality of the group of algebraic cycles. Let f : X → XIf f is flat
Flat morphism
In mathematics, in particular in the theory of schemes in algebraic geometry, a flat morphism f from a scheme X to a scheme Y is a morphism such that the induced map on every stalk is a flat map of rings, i.e.,is a flat map for all P in X...
of some constant relative dimension (i.e. all fibers have the same dimension), we can define for any subvariety Y
which by assumption has the same codimension as Y′.
Conversely, if f is proper, for Y a subvariety of X the pushforward is defined to be
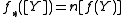
where n is the degree of the extension of function fields
Function field (scheme theory)
In algebraic geometry, the function field KX of a scheme Xis a generalization of the notion of a sheaf of rational functions on a variety. In the case of varieties, such a sheaf associates to each open set U the ring of all rational functions on that open set; in other words, KX is the set of...
[k(Y) : k(f(Y))] if the restriction of f to Y is finite and 0 otherwise.
By linearity, these definitions extend to homomorphisms of abelian groups
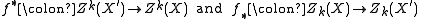
(the latter by virtue of the convention) are homomorphisms of abelian groups. See Chow ring
Chow ring
In algebraic geometry, the Chow ring of an algebraic variety is an algebraic-geometric analogue of the cohomology ring of the variety considered as a topological space: its elements are formed out of actual subvarieties and its multiplicative structure is derived from the intersection of...
for a discussion of the functoriality related to the ring structure.