
Symbol of a differential operator
Encyclopedia
In mathematics
, the symbol of a linear differential operator associates to a differential operator
a polynomial
by, roughly speaking, replacing each partial derivative
by a new variable. The symbol of a differential operator has broad applications to Fourier analysis. In particular, in this connection it leads to the notion of a pseudo-differential operator
. The highest-order terms of the symbol, known as the principal symbol, almost completely controls the qualitative behavior of solutions of a partial differential equation
. Linear elliptic partial differential equations can be characterized as those whose principal symbol is nowhere zero. In the study of hyperbolic
and parabolic partial differential equation
s, zeros of the principal symbol correspond to the characteristics
of the partial differential equation. Consequently, the symbol is often fundamental for the solution of such equations, and are one of the main computational devices used to study their singularities.
Rd. Then P is a polynomial in the derivative D, which in multi-index notation can be written
The total symbol of P is the polynomial p:
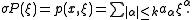
The leading symbol, also known as the principal symbol, is the highest degree component of σP:

and is of importance later because it is the only part of the symbol that transforms as a tensor
under changes to the coordinate system.
The symbol of P appears naturally in connection with the Fourier transform
as follows. Let ƒ be a Schwartz function. Then by the inverse Fourier transform,
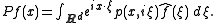
This exhibits P as a Fourier multiplier. A more general class of functions p(x,ξ) which satisfy at most polynomial growth conditions in ξ under which this integral is well-behaved comprises the pseudo-differential operator
s.
s over a closed manifold
X, and suppose
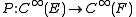
is a differential operator of order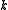 . In local coordinates
. In local coordinates
we have

where, for each multi-index α,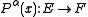 is a bundle map
is a bundle map
, symmetric on the indices α.
The kth order coefficients of P transform as a symmetric tensor
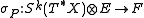
from the tensor product
of the kth symmetric power of the cotangent bundle
of X with E to E. This symmetric tensor is known as the principal symbol (or just the symbol) of P.
The coordinate system xi permits a local trivialization of the cotangent bundle by the coordinate differentials dxi, which determine fiber coordinates ξi. In terms of a basis of frames eμ, fν of E and F, respectively, the differential operator P decomposes into components
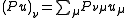
on each section u of E. Here Pνμ is the scalar differential operator defined by
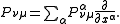
With this trivialization, the principal symbol can now be written
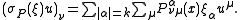
In the cotangent space over a fixed point x of X, the symbol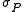 defines a homogeneous polynomial
defines a homogeneous polynomial
of degree k in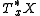 with values in
with values in 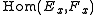 .
.
The differential operator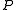 is elliptic if its symbol is invertible; that is for each nonzero
is elliptic if its symbol is invertible; that is for each nonzero 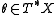 the bundle map
the bundle map 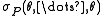 is invertible. On a compact manifold, it follows from the elliptic theory that P is a Fredholm operator
is invertible. On a compact manifold, it follows from the elliptic theory that P is a Fredholm operator
: it has finite dimensional kernel
and cokernel.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the symbol of a linear differential operator associates to a differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
by, roughly speaking, replacing each partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
by a new variable. The symbol of a differential operator has broad applications to Fourier analysis. In particular, in this connection it leads to the notion of a pseudo-differential operator
Pseudo-differential operator
In mathematical analysis a pseudo-differential operator is an extension of the concept of differential operator. Pseudo-differential operators are used extensively in the theory of partial differential equations and quantum field theory....
. The highest-order terms of the symbol, known as the principal symbol, almost completely controls the qualitative behavior of solutions of a partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
. Linear elliptic partial differential equations can be characterized as those whose principal symbol is nowhere zero. In the study of hyperbolic
Hyperbolic partial differential equation
In mathematics, a hyperbolic partial differential equation of order n is a partial differential equation that, roughly speaking, has a well-posed initial value problem for the first n−1 derivatives. More precisely, the Cauchy problem can be locally solved for arbitrary initial data along...
and parabolic partial differential equation
Parabolic partial differential equation
A parabolic partial differential equation is a type of second-order partial differential equation , describing a wide family of problems in science including heat diffusion, ocean acoustic propagation, in physical or mathematical systems with a time variable, and which behave essentially like heat...
s, zeros of the principal symbol correspond to the characteristics
Method of characteristics
In mathematics, the method of characteristics is a technique for solving partial differential equations. Typically, it applies to first-order equations, although more generally the method of characteristics is valid for any hyperbolic partial differential equation...
of the partial differential equation. Consequently, the symbol is often fundamental for the solution of such equations, and are one of the main computational devices used to study their singularities.
Operators on Euclidean space
Let P be a linear differential operator of order k on the Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rd. Then P is a polynomial in the derivative D, which in multi-index notation can be written

The total symbol of P is the polynomial p:
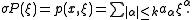
The leading symbol, also known as the principal symbol, is the highest degree component of σP:

and is of importance later because it is the only part of the symbol that transforms as a tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
under changes to the coordinate system.
The symbol of P appears naturally in connection with the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
as follows. Let ƒ be a Schwartz function. Then by the inverse Fourier transform,
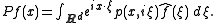
This exhibits P as a Fourier multiplier. A more general class of functions p(x,ξ) which satisfy at most polynomial growth conditions in ξ under which this integral is well-behaved comprises the pseudo-differential operator
Pseudo-differential operator
In mathematical analysis a pseudo-differential operator is an extension of the concept of differential operator. Pseudo-differential operators are used extensively in the theory of partial differential equations and quantum field theory....
s.
Vector bundles
Let E and F be vector bundleVector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
s over a closed manifold
Closed manifold
In mathematics, a closed manifold is a type of topological space, namely a compact manifold without boundary. In contexts where no boundary is possible, any compact manifold is a closed manifold....
X, and suppose
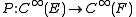
is a differential operator of order
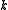 . In local coordinates
. In local coordinatesLocal coordinates
Local coordinates are measurement indices into a local coordinate system or a local coordinate space. A simple example is using house numbers to locate a house on a street; the street is a local coordinate system within a larger system composed of city townships, states, countries, etc.Local...
we have

where, for each multi-index α,
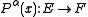 is a bundle map
is a bundle mapBundle map
In mathematics, a bundle map is a morphism in the category of fiber bundles. There are two distinct, but closely related, notions of bundle map, depending on whether the fiber bundles in question have a common base space. There are also several variations on the basic theme, depending on precisely...
, symmetric on the indices α.
The kth order coefficients of P transform as a symmetric tensor
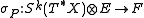
from the tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
of the kth symmetric power of the cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
of X with E to E. This symmetric tensor is known as the principal symbol (or just the symbol) of P.
The coordinate system xi permits a local trivialization of the cotangent bundle by the coordinate differentials dxi, which determine fiber coordinates ξi. In terms of a basis of frames eμ, fν of E and F, respectively, the differential operator P decomposes into components
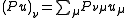
on each section u of E. Here Pνμ is the scalar differential operator defined by
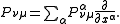
With this trivialization, the principal symbol can now be written
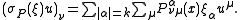
In the cotangent space over a fixed point x of X, the symbol
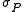 defines a homogeneous polynomial
defines a homogeneous polynomialHomogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
of degree k in
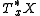 with values in
with values in 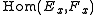 .
.The differential operator
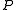 is elliptic if its symbol is invertible; that is for each nonzero
is elliptic if its symbol is invertible; that is for each nonzero 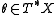 the bundle map
the bundle map 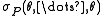 is invertible. On a compact manifold, it follows from the elliptic theory that P is a Fredholm operator
is invertible. On a compact manifold, it follows from the elliptic theory that P is a Fredholm operatorFredholm operator
In mathematics, a Fredholm operator is an operator that arises in the Fredholm theory of integral equations. It is named in honour of Erik Ivar Fredholm....
: it has finite dimensional kernel
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
and cokernel.
See also
- Multiplier (Fourier analysis)Multiplier (Fourier analysis)In Fourier analysis, a multiplier operator is a type of linear operator, or transformation of functions. These operators act on a function by altering its Fourier transform. Specifically they multiply the Fourier transform of a function by a specified function known as the multiplier or symbol...
- Atiyah-Singer index theorem (section on symbol of operator)

