Pseudo-differential operator
Encyclopedia
In mathematical analysis
a pseudo-differential operator is an extension of the concept of differential operator
. Pseudo-differential operators are used extensively in the theory of partial differential equations and quantum field theory
.
with constant coefficients,
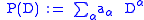
which acts on smooth functions
with compact support in Rn.
This operator can be written as a composition of a Fourier transform
, a simple multiplication by the
polynomial function (called the symbol)
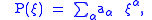
and an inverse Fourier transform, in the form:
Here,
α = (α1, … ,αn) is a multi-index, aα are complex numbers, and
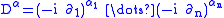
is an iterated partial derivative, where ∂j means differentiation with respect to the j-th variable.
Similarly, a pseudo-differential operator P(x,D) on Rn is an operator of the form
with a more general function P in the integrand, with certain properties to be specified.
Derivation of formula
The Fourier transform of a smooth function u, compactly supported in Rn, is
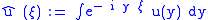
and Fourier's inversion formula gives
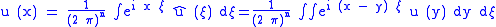
By applying P(D) to this representation of u and using
one obtains formula .
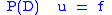
we (formally) apply the Fourier transform on both sides and obtain the algebraic equation
.
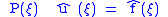If the symbol P(ξ) is never zero when ξ ∈ Rn, then it is possible to divide by P(ξ):
By Fourier's inversion formula, a solution is
.
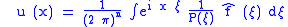Here it is assumed that:
The last assumption can be weakened by using the theory of distribution
s.
The first two assumptions can be weakened as follows.
In the last formula, write out the Fourier transform of ƒ to obtain
.
This is similar to formula , except that 1/P(ξ) is not a polynomial function, but a function of a more general kind.
One assumes that the symbol P(x,ξ) belongs to a certain symbol class.
For instance, if P(x,ξ) is an infinitely differentiable function on Rn × Rn with the property
for all x,ξ ∈Rn, all multiindices α,β. some constants Cα, β and some real number m, then P belongs to the symbol class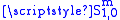
of Hörmander. The corresponding operator P(x,D) is called a pseudo-differential operator of order m and belongs to the class
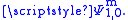
operators of order m.
The composition PQ of two pseudo-differential operators P, Q is again a pseudo-differential operator and the symbol of PQ can be calculated by using the symbols of P and Q. The adjoint and transpose of a pseudo-differential operator is a pseudo-differential operator.
If a differential operator of order m is (uniformly) elliptic (of order m)
and invertible, then its inverse is a pseudo-differential operator of order −m, and its symbol can be calculated. This means that one can solve linear elliptic differential equations more or less explicitly
by using the theory of pseudo-differential operators.
Differential operators are local in the sense that one only needs the value of a function in a neighbourhood of a point to determine the effect of the operator. Pseudo-differential operators are pseudo-local, which means informally that when applied to a distribution they do not create a singularity at points where the distribution was already smooth.
Just as a differential operator can be expressed in terms of D = −id/dx in the form
for a polynomial
p in D (which is called the symbol), a pseudo-differential operator has a symbol in a more general class of functions. Often one can reduce a problem in analysis of pseudo-differential operators to a sequence of algebraic problems involving their symbols, and this is the essence of microlocal analysis
.
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
a pseudo-differential operator is an extension of the concept of differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
. Pseudo-differential operators are used extensively in the theory of partial differential equations and quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
.
Linear Differential Operators with Constant Coefficients
Consider a linear differential operatorDifferential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
with constant coefficients,
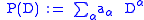
which acts on smooth functions
with compact support in Rn.This operator can be written as a composition of a Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
, a simple multiplication by the
polynomial function (called the symbol)
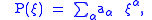
and an inverse Fourier transform, in the form:
Here,
α = (α1, … ,αn) is a multi-index, aα are complex numbers, and
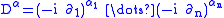
is an iterated partial derivative, where ∂j means differentiation with respect to the j-th variable.
Similarly, a pseudo-differential operator P(x,D) on Rn is an operator of the form
with a more general function P in the integrand, with certain properties to be specified.
Derivation of formula
The Fourier transform of a smooth function u, compactly supported in Rn, is
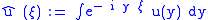
and Fourier's inversion formula gives
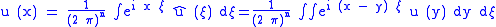
By applying P(D) to this representation of u and using
one obtains formula .
Representation of Solutions to Partial Differential Equations
To solve the partial differential equation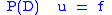we (formally) apply the Fourier transform on both sides and obtain the algebraic equation
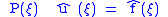.If the symbol P(ξ) is never zero when ξ ∈ Rn, then it is possible to divide by P(ξ):
By Fourier's inversion formula, a solution is
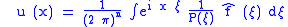.Here it is assumed that:
- P(D) is a linear differential operator with constant coefficients,
- its symbol P(ξ) is never zero,
- both u and ƒ have a well defined Fourier transform.
The last assumption can be weakened by using the theory of distribution
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
s.
The first two assumptions can be weakened as follows.
In the last formula, write out the Fourier transform of ƒ to obtain
.This is similar to formula , except that 1/P(ξ) is not a polynomial function, but a function of a more general kind.
Symbol Classes and Pseudo-Differential Operators
The main idea is to define operators P(x,D) by using formula (1) and admitting more general symbols P(x,ξ):One assumes that the symbol P(x,ξ) belongs to a certain symbol class.
For instance, if P(x,ξ) is an infinitely differentiable function on Rn × Rn with the property
for all x,ξ ∈Rn, all multiindices α,β. some constants Cα, β and some real number m, then P belongs to the symbol class
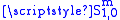of Hörmander. The corresponding operator P(x,D) is called a pseudo-differential operator of order m and belongs to the class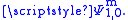Properties
Linear differential operators of order m with smooth bounded coefficients are pseudo-differentialoperators of order m.
The composition PQ of two pseudo-differential operators P, Q is again a pseudo-differential operator and the symbol of PQ can be calculated by using the symbols of P and Q. The adjoint and transpose of a pseudo-differential operator is a pseudo-differential operator.
If a differential operator of order m is (uniformly) elliptic (of order m)
and invertible, then its inverse is a pseudo-differential operator of order −m, and its symbol can be calculated. This means that one can solve linear elliptic differential equations more or less explicitly
by using the theory of pseudo-differential operators.
Differential operators are local in the sense that one only needs the value of a function in a neighbourhood of a point to determine the effect of the operator. Pseudo-differential operators are pseudo-local, which means informally that when applied to a distribution they do not create a singularity at points where the distribution was already smooth.
Just as a differential operator can be expressed in terms of D = −id/dx in the form
for a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
p in D (which is called the symbol), a pseudo-differential operator has a symbol in a more general class of functions. Often one can reduce a problem in analysis of pseudo-differential operators to a sequence of algebraic problems involving their symbols, and this is the essence of microlocal analysis
Microlocal analysis
In mathematical analysis, microlocal analysis comprises techniques developed from the 1950s onwards based on Fourier transforms related to the study of variable-coefficients-linear and nonlinear partial differential equations...
.
See also
- Differential algebraDifferential algebraIn mathematics, differential rings, differential fields, and differential algebras are rings, fields, and algebras equipped with a derivation, which is a unary function that is linear and satisfies the Leibniz product law...
for a definition of pseudo-differential operators in the context of differential algebras and differential rings. - Fourier transformFourier transformIn mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
- Fourier integral operatorFourier integral operatorIn mathematical analysis, Fourier integral operators have become an important tool in the theory of partial differential equations. The class of Fourier integral operators contains differential operators as well as classical integral operators as special cases....
- Oscillatory integral operator
- Sato's fundamental theorem
Further reading
Here are some of the standard reference books- Michael E. Taylor, Pseudodifferential Operators, Princeton Univ. Press 1981. ISBN 0-691-08282-0
- M. A. Shubin, Pseudodifferential Operators and Spectral Theory, Springer-Verlag 2001. ISBN 3-540-41195-X
- Francois Treves, Introduction to Pseudo Differential and Fourier Integral Operators, (University Series in Mathematics), Plenum Publ. Co. 1981. ISBN 0-306-40404-4
- F. G. Friedlander and M. Joshi, Introduction to the Theory of Distributions, Cambridge University Press 1999. ISBN 0-521-64971-4
External links
- Lectures on Pseudo-differential Operators by Mark S. JoshiMark S. JoshiMark S. Joshi is a researcher and consultant in mathematical finance. He obtained a B.A. in mathematics from the University of Oxford in 1990, and a Ph.D. in pure mathematics from the Massachusetts Institute of Technology in 1994 under the supervision of Richard Melrose...
on arxiv.org.