
Stress-energy-momentum pseudotensor
Encyclopedia
In the theory of general relativity
, a stress–energy–momentum pseudotensor, such as the Landau–Lifshitz pseudotensor, is an extension of the non-gravitational stress–energy tensor which incorporates the energy-momentum of gravity. It allows the energy-momentum of a system of gravitating matter to be defined. In particular it allows the total of matter plus the gravitating energy-momentum to form a conserved current
within the framework of general relativity
, so that the total energy-momentum crossing the hypersurface
(3-dimensional boundary) of any compact space-time hypervolume (4-dimensional submanifold) vanishes.
Some people object to this derivation on the grounds that pseudotensor
s are inappropriate objects in general relativity, but the conservation law only requires the use of the 4-divergence
of a pseudotensor which is, in this case, a tensor (which also vanishes). Also, most pseudotensors are sections of jet bundle
s, which are perfectly valid objects in GR.
allows the energy-momentum conservation laws to be extended into general relativity
. Subtraction of the matter stress–energy–momentum tensor from the combined pseudotensor results in the gravitational stress–energy–momentum pseudotensor.
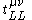 :
:
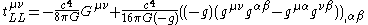
where:
,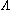 , was zero. Nowadays we don't make that assumption
, was zero. Nowadays we don't make that assumption
, and the expression needs the addition of a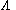 term, giving:
term, giving:
This is necessary for consistency with the Einstein field equations
.
This definition of energy-momentum is covariantly applicable not just under Lorentz transformations, but also under general coordinate transformations.
Paul Dirac
showed that the mixed Einstein pseudotensor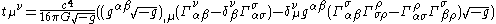
satisfies a conservation law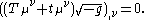
Clearly this pseudotensor for gravitational stress-energy is constructed exclusively from the metric tensor and its first derivatives. Consequently it vanishes at any event when the coordinate system is chosen to make the first derivatives of the metric vanish because each term in the pseudotensor is quadratic in the first derivatives of the metric. However it is not symmetric, and is therefore not suitable for basing a definition of angular momentum on.
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, a stress–energy–momentum pseudotensor, such as the Landau–Lifshitz pseudotensor, is an extension of the non-gravitational stress–energy tensor which incorporates the energy-momentum of gravity. It allows the energy-momentum of a system of gravitating matter to be defined. In particular it allows the total of matter plus the gravitating energy-momentum to form a conserved current
Conserved current
In physics a conserved current is a current, j^\mu, that satisfies the continuity equation \partial_\mu j^\mu=0. The continuity equation represents a conservation law, hence the name....
within the framework of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, so that the total energy-momentum crossing the hypersurface
Hypersurface
In geometry, a hypersurface is a generalization of the concept of hyperplane. Suppose an enveloping manifold M has n dimensions; then any submanifold of M of n − 1 dimensions is a hypersurface...
(3-dimensional boundary) of any compact space-time hypervolume (4-dimensional submanifold) vanishes.
Some people object to this derivation on the grounds that pseudotensor
Pseudotensor
In physics and mathematics, a pseudotensor is usually a quantity that transforms like a tensor under an orientation preserving coordinate transformation , but gains an additional sign flip under an orientation reversing coordinate transformation In physics and mathematics, a pseudotensor is usually...
s are inappropriate objects in general relativity, but the conservation law only requires the use of the 4-divergence
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
of a pseudotensor which is, in this case, a tensor (which also vanishes). Also, most pseudotensors are sections of jet bundle
Jet bundle
In differential geometry, the jet bundle is a certain construction which makes a new smooth fiber bundle out of a given smooth fiber bundle. It makes it possible to write differential equations on sections of a fiber bundle in an invariant form...
s, which are perfectly valid objects in GR.
Landau–Lifshitz pseudotensor
The use of the Landau–Lifshitz combined matter+gravitational stress–energy–momentum pseudotensorPseudotensor
In physics and mathematics, a pseudotensor is usually a quantity that transforms like a tensor under an orientation preserving coordinate transformation , but gains an additional sign flip under an orientation reversing coordinate transformation In physics and mathematics, a pseudotensor is usually...
allows the energy-momentum conservation laws to be extended into general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
. Subtraction of the matter stress–energy–momentum tensor from the combined pseudotensor results in the gravitational stress–energy–momentum pseudotensor.
Requirements
Landau & Lifshitz were led by four requirements in their search for a gravitational energy momentum pseudotensor, :
:
- that it be constructed entirely from the metric tensorMetric tensor (general relativity)In general relativity, the metric tensor is the fundamental object of study. It may loosely be thought of as a generalization of the gravitational field familiar from Newtonian gravitation...
, so as to be purely geometrical or gravitational in origin. - that it be index symmetric , i.e.
 , (to conserve angular momentumAngular momentumIn physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
, (to conserve angular momentumAngular momentumIn physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
) - that, when added to the stress–energy tensor of matter,
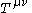 , its total 4-divergenceDivergenceIn vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
, its total 4-divergenceDivergenceIn vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
vanishes (this is required of any conserved currentConserved currentIn physics a conserved current is a current, j^\mu, that satisfies the continuity equation \partial_\mu j^\mu=0. The continuity equation represents a conservation law, hence the name....
) so that we have a conserved expression for the total stress–energy–momentum. - that it vanish locally in an inertial frame of referenceInertial frame of referenceIn physics, an inertial frame of reference is a frame of reference that describes time homogeneously and space homogeneously, isotropically, and in a time-independent manner.All inertial frames are in a state of constant, rectilinear motion with respect to one another; they are not...
(which requires that it only contains first and not second or higher derivativeDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s of the metric). This is because the equivalence principleEquivalence principleIn the physics of general relativity, the equivalence principle is any of several related concepts dealing with the equivalence of gravitational and inertial mass, and to Albert Einstein's assertion that the gravitational "force" as experienced locally while standing on a massive body is actually...
requires that the gravitational force field, the Christoffel symbolsChristoffel symbolsIn mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...
, vanish locally in some frame. If gravitational energy is a function of its force field, as is usual for other forces, then the associated gravitational pseudotensor should also vanish locally.
Definition
Landau and Lifshitz showed that there is a unique construction that satisfies these requirements, namely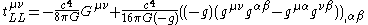
where:
- Gμν is the Einstein tensorEinstein tensorIn differential geometry, the Einstein tensor , named after Albert Einstein, is used to express the curvature of a Riemannian manifold...
(which is constructed from the metric)
- gμν is the inverse of the metric tensorMetric tensor (general relativity)In general relativity, the metric tensor is the fundamental object of study. It may loosely be thought of as a generalization of the gravitational field familiar from Newtonian gravitation...
- g = det(gμν) is the determinantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the metric tensor and is < 0. Hence its appearance as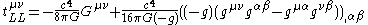 .
.
-
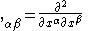 are partial derivativePartial derivativeIn mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
are partial derivativePartial derivativeIn mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s, not covariant derivativeCovariant derivativeIn mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
s.
- G is Newton's gravitational constantGravitational constantThe gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
.
Verification
Examining the 4 requirement conditions we can see that the first 3 are relatively easy to demonstrate:- Since the Einstein tensor,
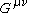 , is itself constructed from the metric, so therefore is
, is itself constructed from the metric, so therefore is 
- Since the Einstein tensor,
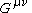 , is symmetric so is
, is symmetric so is  since the additional terms are symmetric by inspection.
since the additional terms are symmetric by inspection. - The Landau–Lifshitz pseudotensor is constructed so that when added to the stress–energy tensor of matter,
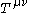 , its total 4-divergenceDivergenceIn vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
, its total 4-divergenceDivergenceIn vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
vanishes: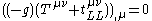 . This follows from the cancellation of the Einstein tensor,
. This follows from the cancellation of the Einstein tensor, 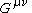 , with the stress–energy tensor,
, with the stress–energy tensor, 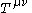 by the Einstein field equationsEinstein field equationsThe Einstein field equations or Einstein's equations are a set of ten equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy...
by the Einstein field equationsEinstein field equationsThe Einstein field equations or Einstein's equations are a set of ten equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy...
; the remaining term vanishes algebraically due the commutativity of partial derivatives applied across antisymmetric indices. - The Landau–Lifshitz pseudotensor appears to include second derivative terms in the metric, but in fact the explicit second derivative terms in the pseudotensor cancel with the implicit second derivative terms contained within the Einstein tensorEinstein tensorIn differential geometry, the Einstein tensor , named after Albert Einstein, is used to express the curvature of a Riemannian manifold...
,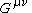 . This is more evident when the pseudotensor is directly expressed in terms of the metric tensor or the Levi-Civita connectionLevi-Civita connectionIn Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle preserving a given Riemannian metric.The fundamental theorem of...
. This is more evident when the pseudotensor is directly expressed in terms of the metric tensor or the Levi-Civita connectionLevi-Civita connectionIn Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle preserving a given Riemannian metric.The fundamental theorem of...
; only the first derivative terms in the metric survive and these vanish where the frame is locally inertial at any chosen point. As a result the entire pseudotensor vanishes locally (again, at any chosen point)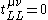 , which demonstrates the delocalisation of gravitational energy-momentum.
, which demonstrates the delocalisation of gravitational energy-momentum.
Cosmological constant
When the Landau–Lifshitz pseudotensor was formulated it was commonly assumed that the cosmological constantCosmological constant
In physical cosmology, the cosmological constant was proposed by Albert Einstein as a modification of his original theory of general relativity to achieve a stationary universe...
,
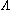 , was zero. Nowadays we don't make that assumption
, was zero. Nowadays we don't make that assumptionAccelerating universe
The accelerating universe is the observation that the universe appears to be expanding at an increasing rate, which in formal terms means that the cosmic scale factor a has a positive second derivative, implying that the velocity at which a given galaxy is receding from us should be continually...
, and the expression needs the addition of a
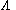 term, giving:
term, giving:
This is necessary for consistency with the Einstein field equations
Einstein field equations
The Einstein field equations or Einstein's equations are a set of ten equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy...
.
Metric and affine connection versions
Landau & Lifshitz also provide two equivalent but longer expressions for the Landau–Lifshitz pseudotensor:- Metric tensorMetric tensorIn the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
version: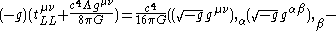
-
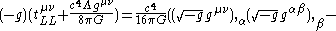
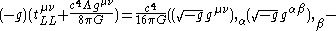
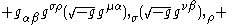
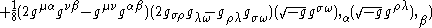
- Affine connectionChristoffel symbolsIn mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...
version: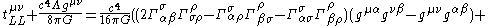
- Affine connection
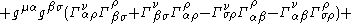

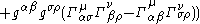
This definition of energy-momentum is covariantly applicable not just under Lorentz transformations, but also under general coordinate transformations.
Einstein pseudotensor
This pseudotensor was originally developed by Albert Einstein.Paul Dirac
Paul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
showed that the mixed Einstein pseudotensor
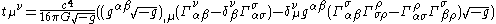
satisfies a conservation law
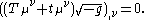
Clearly this pseudotensor for gravitational stress-energy is constructed exclusively from the metric tensor and its first derivatives. Consequently it vanishes at any event when the coordinate system is chosen to make the first derivatives of the metric vanish because each term in the pseudotensor is quadratic in the first derivatives of the metric. However it is not symmetric, and is therefore not suitable for basing a definition of angular momentum on.

