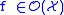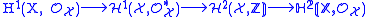Stein manifold
Encyclopedia
In mathematics
, a Stein manifold in the theory of several complex variables
and complex manifold
s is a complex submanifold
of the vector space
of n complex
dimensions. The name is for Karl Stein
.
 of complex dimension
of complex dimension  is called a Stein manifold if the following conditions hold:
is called a Stein manifold if the following conditions hold:
Another result, attributed to Grauert and Röhrl (1956), states moreover that every holomorphic vector bundle on X is trivial.
In particular, every line bundle is trivial, so . The exponential sheaf sequence
. The exponential sheaf sequence
leads to the following exact sequence:
Now Cartan's theorem B shows that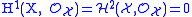 , therefore
, therefore 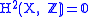 .
.
This is related to the solution of the Cousin problems
, and more precisely to the second Cousin problem.
These facts imply that a Stein manifold is a closed complex submanifold of complex space, whose complex structure is that of the ambient space
(because the embedding is biholomorphic).
Numerous further characterizations of such manifolds exist, in particular capturing the property of their having "many" holomorphic function
s taking values in the complex numbers. See for example Cartan's theorems A and B
, relating to sheaf cohomology
. The initial impetus was to have a description of the properties of the domain of definition of the (maximal) analytic continuation
of an analytic function
.
In the GAGA
set of analogies, Stein manifolds correspond to affine varieties.
Stein manifolds are in some sense dual to the elliptic manifolds in complex analysis which admit "many" holomorphic functions from the complex numbers into themselves. It is known that a Stein manifold is elliptic if and only if it is fibrant
in the sense of so-called "holomorphic homotopy theory".
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Stein manifold in the theory of several complex variables
Several complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
and complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
s is a complex submanifold
Submanifold
In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
of the vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
of n complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
dimensions. The name is for Karl Stein
Karl Stein (mathematician)
Karl Stein was a German mathematician. He is well known for complex analysis and cryptography...
.
Definition
A complex manifoldComplex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
 of complex dimension
of complex dimension  is called a Stein manifold if the following conditions hold:
is called a Stein manifold if the following conditions hold:-
 is holomorphically convex, i.e. for every compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
is holomorphically convex, i.e. for every compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
subset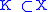 , the so-called holomorphic convex hull,
, the so-called holomorphic convex hull,
- is again a compact subset of
 . Here
. Here 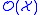 denotes the ring of holomorphic functions on
denotes the ring of holomorphic functions on  .
.
-
 is holomorphically separable, i.e. if
is holomorphically separable, i.e. if  are two points in
are two points in  , then there is a holomorphic function
, then there is a holomorphic function
- such that

Non-compact Riemann surfaces are Stein
Let X be a connected non-compact Riemann surface. A deep theorem of Behnke and Stein (1948) asserts that X is a Stein manifold.Another result, attributed to Grauert and Röhrl (1956), states moreover that every holomorphic vector bundle on X is trivial.
In particular, every line bundle is trivial, so
 . The exponential sheaf sequence
. The exponential sheaf sequenceExponential sheaf sequence
In mathematics, the exponential sheaf sequence is a fundamental short exact sequence of sheaves used in complex geometry.Let M be a complex manifold, and write OM for the sheaf of holomorphic functions on M. Let OM* be the subsheaf consisting of the non-vanishing holomorphic functions. These are...
leads to the following exact sequence:
Now Cartan's theorem B shows that
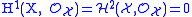 , therefore
, therefore 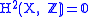 .
.This is related to the solution of the Cousin problems
Cousin problems
In mathematics, the Cousin problems are two questions in several complex variables, concerning the existence of meromorphic functions that are specified in terms of local data. They were introduced in special cases by P. Cousin in 1895...
, and more precisely to the second Cousin problem.
Properties and examples of Stein manifolds
- The standard complex space
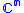 is a Stein manifold.
is a Stein manifold. - It can be shown quite easily that every closed complex submanifold of a Stein manifold is a Stein manifold, too.
- The embedding theorem for Stein manifolds states the following: Every Stein manifold
 of complex dimension
of complex dimension  can be embedded into
can be embedded into 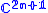 by a biholomorphic proper mapProper mapIn mathematics, a continuous function between topological spaces is called proper if inverse images of compact subsets are compact. In algebraic geometry, the analogous concept is called a proper morphism.- Definition :...
by a biholomorphic proper mapProper mapIn mathematics, a continuous function between topological spaces is called proper if inverse images of compact subsets are compact. In algebraic geometry, the analogous concept is called a proper morphism.- Definition :...
.
These facts imply that a Stein manifold is a closed complex submanifold of complex space, whose complex structure is that of the ambient space
Ambient space
An ambient space, ambient configuration space, or electroambient space, is the space surrounding an object.-Mathematics:In mathematics, especially in geometry and topology, an ambient space is the space surrounding a mathematical object...
(because the embedding is biholomorphic).
- In one complex dimension the Stein condition can be simplified: a connected Riemann surfaceRiemann surfaceIn mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
is a Stein manifold if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it is not compact. This can be proved using a version of the Runge theorem for Riemann surfaces, due to Behnke and Stein. - Every Stein manifold
 is holomorphically spreadable, i.e. for every point
is holomorphically spreadable, i.e. for every point 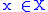 , there are
, there are  holomorphic functions defined on all of
holomorphic functions defined on all of  which form a local coordinate system when restricted to some open neighborhood of
which form a local coordinate system when restricted to some open neighborhood of  .
. - Being a Stein manifold is equivalent to being a (complex) strongly pseudoconvex manifold. The latter means that it has a strongly pseudoconvex (or plurisubharmonicPlurisubharmonic functionIn mathematics, plurisubharmonic functions form an important class of functions used in complex analysis. On a Kähler manifold, plurisubharmonic functions form a subset of the subharmonic functions...
) exhaustive function, i.e. a smooth real function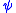 on
on  (which can be assumed to be a Morse functionMorse theoryIn differential topology, the techniques of Morse theory give a very direct way of analyzing the topology of a manifold by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a differentiable function on a manifold will, in a typical case, reflect...
(which can be assumed to be a Morse functionMorse theoryIn differential topology, the techniques of Morse theory give a very direct way of analyzing the topology of a manifold by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a differentiable function on a manifold will, in a typical case, reflect...
) with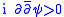 , such that the subsets
, such that the subsets  are compact in
are compact in  for every real number
for every real number  . This is a solution to the so-called Levi problem, named after E. E. Levi (1911). The function
. This is a solution to the so-called Levi problem, named after E. E. Levi (1911). The function 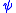 invites a generalization of Stein manifold to the idea of a corresponding class of compact complex manifolds with boundary called Stein domains. A Stein domain is the preimage
invites a generalization of Stein manifold to the idea of a corresponding class of compact complex manifolds with boundary called Stein domains. A Stein domain is the preimage  . Some authors call such manifolds therefore strictly pseudoconvex manifolds.
. Some authors call such manifolds therefore strictly pseudoconvex manifolds. - Related to the previous item, another equivalent and more topological definition in complex dimension 2 is the following: a Stein surface is a complex surface X with a real-valued Morse function f on X such that, away from the critical points of f, the field of complex tangencies to the preimage Xc = f−1(c) is a contact structureContact geometryIn mathematics, contact geometry is the study of a geometric structure on smooth manifolds given by a hyperplane distribution in the tangent bundle and specified by a one-form, both of which satisfy a 'maximum non-degeneracy' condition called 'complete non-integrability'...
that induces an orientation on Xc agreeing with the usual orientation as the boundary of f−1(−∞,c). That is, f−1(−∞,c) is a Stein fillingSymplectic fillingIn mathematics, a filling of a manifold X is a cobordism W between X and the empty set. More to the point, the n-dimensional topological manifold X is the boundary of an n+1-dimensional manifold W...
of Xc.
Numerous further characterizations of such manifolds exist, in particular capturing the property of their having "many" holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s taking values in the complex numbers. See for example Cartan's theorems A and B
Cartan's theorems A and B
In mathematics, Cartan's theorems A and B are two results proved by Henri Cartan around 1951, concerning a coherent sheaf F on a Stein manifold X. They are significant both as applied to several complex variables, and in the general development of sheaf cohomology.Theorem A states that F is spanned...
, relating to sheaf cohomology
Sheaf cohomology
In mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
. The initial impetus was to have a description of the properties of the domain of definition of the (maximal) analytic continuation
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
of an analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
.
In the GAGA
Gaga
- Entertainment :* Lady Gaga , American recording artist* Gaga , a dancing technique* Rara, a type of Caribbean music called Gaga in the Dominican Republic* GNZ-004 Gaga, a mobile weapon in Mobile Suit Gundam 00- Sports :...
set of analogies, Stein manifolds correspond to affine varieties.
Stein manifolds are in some sense dual to the elliptic manifolds in complex analysis which admit "many" holomorphic functions from the complex numbers into themselves. It is known that a Stein manifold is elliptic if and only if it is fibrant
Fibrant object
In mathematics, specifically in homotopy theory in the context of a model category M, a fibrant object A of M is an object that has a fibration to the terminal object of the category.-Properties:...
in the sense of so-called "holomorphic homotopy theory".