Statistical physics
Encyclopedia
Statistical physics is the branch of physics
that uses methods of probability theory
and statistics
, and particularly the mathematical
tools for dealing with large populations and approximations, in solving physical problems. It can describe a wide variety of fields with an inherently stochastic
nature. Its applications include many problems in the fields of physics, biology
, chemistry
, neurology
, and even some social sciences, such as sociology
. Its main purpose is to clarify the properties of matter in aggregate, in terms of physical laws governing atomic motion.
In particular, statistical mechanics
develops the phenomenological results of thermodynamics
from a probabilistic examination of the underlying microscopic systems. Historically, one of the first topics in physics where statistical methods were applied was the field of mechanics
, which is concerned with the motion of particles or objects when subjected to a force.
provides a framework for relating the microscopic properties of individual atoms and molecules to the macroscopic or bulk properties of materials that can be observed in everyday life, therefore explaining thermodynamics
as a natural result of statistics, classical mechanics
, and quantum mechanics
at the microscopic level. Because of this history, the statistical physics is often considered synonymous with statistical mechanics or statistical thermodynamics.This article presents a broader sense of the definition of statistical physics
One of the most important equations in Statistical mechanics (analogous to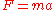
in mechanics, or the Schroedinger equation in quantum mechanics ) is the definition of the partition function 
, which is essentially a weighted sum of all possible states 
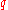available to a system.
where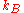
is the Boltzmann constant, 
is temperature
and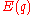
is energy
of state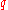
. Furthermore, the probability of a given state, 
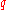, occurring is given by
Here we see that very-high-energy states have little probability of occurring, a result that is consistent with intuition.
A statistical approach can work well in classical systems when the number of degrees of freedom
(and so the number of variables) is so large that exact solution is not possible, or not really useful. Statistical mechanics can also describe work in non-linear dynamics, chaos theory
, thermal physics
, fluid dynamics
(particularly at high Knudsen number
s), or plasma physics.
Although some problems in statistical physics can be solved analytically using approximations and expansions, most current research utilizes the large processing power of modern computers to simulate or approximate solutions. A common approach to statistical problems is to use a Monte Carlo simulation to yield insight into the dynamics of a complex system.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
that uses methods of probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, and particularly the mathematical
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
tools for dealing with large populations and approximations, in solving physical problems. It can describe a wide variety of fields with an inherently stochastic
Stochastic
Stochastic refers to systems whose behaviour is intrinsically non-deterministic. A stochastic process is one whose behavior is non-deterministic, in that a system's subsequent state is determined both by the process's predictable actions and by a random element. However, according to M. Kac and E...
nature. Its applications include many problems in the fields of physics, biology
Biology
Biology is a natural science concerned with the study of life and living organisms, including their structure, function, growth, origin, evolution, distribution, and taxonomy. Biology is a vast subject containing many subdivisions, topics, and disciplines...
, chemistry
Chemistry
Chemistry is the science of matter, especially its chemical reactions, but also its composition, structure and properties. Chemistry is concerned with atoms and their interactions with other atoms, and particularly with the properties of chemical bonds....
, neurology
Neurology
Neurology is a medical specialty dealing with disorders of the nervous system. Specifically, it deals with the diagnosis and treatment of all categories of disease involving the central, peripheral, and autonomic nervous systems, including their coverings, blood vessels, and all effector tissue,...
, and even some social sciences, such as sociology
Sociology
Sociology is the study of society. It is a social science—a term with which it is sometimes synonymous—which uses various methods of empirical investigation and critical analysis to develop a body of knowledge about human social activity...
. Its main purpose is to clarify the properties of matter in aggregate, in terms of physical laws governing atomic motion.
In particular, statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
develops the phenomenological results of thermodynamics
Thermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
from a probabilistic examination of the underlying microscopic systems. Historically, one of the first topics in physics where statistical methods were applied was the field of mechanics
Mechanics
Mechanics is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment....
, which is concerned with the motion of particles or objects when subjected to a force.
Statistical mechanics
Statistical mechanicsStatistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
provides a framework for relating the microscopic properties of individual atoms and molecules to the macroscopic or bulk properties of materials that can be observed in everyday life, therefore explaining thermodynamics
Thermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
as a natural result of statistics, classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, and quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
at the microscopic level. Because of this history, the statistical physics is often considered synonymous with statistical mechanics or statistical thermodynamics.This article presents a broader sense of the definition of statistical physics
One of the most important equations in Statistical mechanics (analogous to
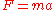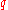in mechanics, or the Schroedinger equation in quantum mechanics ) is the definition of the partition function , which is essentially a weighted sum of all possible states available to a system.
where
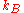is the Boltzmann constant, is temperatureTemperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
and
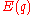is energyEnergy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
of state
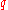. Furthermore, the probability of a given state, 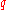, occurring is given by
Here we see that very-high-energy states have little probability of occurring, a result that is consistent with intuition.
A statistical approach can work well in classical systems when the number of degrees of freedom
Degrees of freedom (physics and chemistry)
A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...
(and so the number of variables) is so large that exact solution is not possible, or not really useful. Statistical mechanics can also describe work in non-linear dynamics, chaos theory
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
, thermal physics
Thermal physics
Thermal physics is the combined study of thermodynamics, statistical mechanics, and kinetic theory. This umbrella-subject is typically designed for physics students and functions to provide a general introduction to each of three core heat-related subjects...
, fluid dynamics
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
(particularly at high Knudsen number
Knudsen number
The Knudsen number is a dimensionless number defined as the ratio of the molecular mean free path length to a representative physical length scale. This length scale could be, for example, the radius of a body in a fluid...
s), or plasma physics.
Although some problems in statistical physics can be solved analytically using approximations and expansions, most current research utilizes the large processing power of modern computers to simulate or approximate solutions. A common approach to statistical problems is to use a Monte Carlo simulation to yield insight into the dynamics of a complex system.
See also
- Statistical ensembleStatistical ensemble (mathematical physics)In mathematical physics, especially as introduced into statistical mechanics and thermodynamics by J. Willard Gibbs in 1878, an ensemble is an idealization consisting of a large number of mental copies of a system, considered all at once, each of which represents a possible state that the real...
- Statistical field theoryStatistical field theoryA statistical field theory is any model in statistical mechanics where the degrees of freedom comprise a field or fields. In other words, the microstates of the system are expressed through field configurations...
- Mean sojourn timeMean sojourn timeThe mean sojourn time for an object in a system is a mathematical term for the amount of time an object is expected to spend in a system before leaving the system for good.- Calculation :...
- Dynamics of Markovian particlesDynamics of Markovian ParticlesDynamics of Markovian particles is the basis of a theory for kinetics of particles in open heterogeneous systems. It can be looked upon as an application of the notion of stochastic process conceived as a physical entity; e.g...
- Complex networkComplex networkIn the context of network theory, a complex network is a graph with non-trivial topological features—features that do not occur in simple networks such as lattices or random graphs but often occur in real graphs...
- Mathematical physicsMathematical physicsMathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
- Combinatorics and physicsCombinatorics and physicsCombinatorial physics or physical combinatorics is the area of interaction between physics and combinatorics."Combinatorial Physics is an emerging area which unites combinatorial and discrete mathematical techniques applied to theoretical physics, especially Quantum Theory."."Physical combinatorics...