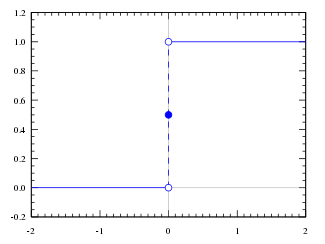
Heaviside step function - AbsoluteAstronomy.com

The Heaviside step function, or the unit step function, usually denoted by H (but sometimes u or θ), is a discontinuous

Continuous function

In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...

function

Function (mathematics)

In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

whose value is zero

0 (number)

0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...

for negative argument and one for positive argument.
It seldom matters what value is used for H(0), since is mostly used as a distribution

Distribution (mathematics)

In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...

. Some common choices can be seen below.

The function is used in the mathematics of control theory

Control theory

Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...

and signal processing

Signal processing

Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...

to represent a signal that switches on at a specified time and stays switched on indefinitely. It is also used in structural mechanics

Structural mechanics

Structural mechanics or Mechanics of structures is the computation of deformations, deflections, and internal forces or stresses within structures, either for design or for performance evaluation of existing structures. It is one subset of structural analysis...

together with the Dirac delta function

Dirac delta function

The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...

to describe different types of structural loads. It was named after the English

England

England is a country that is part of the United Kingdom. It shares land borders with Scotland to the north and Wales to the west; the Irish Sea is to the north west, the Celtic Sea to the south west, with the North Sea to the east and the English Channel to the south separating it from continental...

polymath

Polymath

A polymath is a person whose expertise spans a significant number of different subject areas. In less formal terms, a polymath may simply be someone who is very knowledgeable...

Oliver Heaviside

Oliver Heaviside was a self-taught English electrical engineer, mathematician, and physicist who adapted complex numbers to the study of electrical circuits, invented mathematical techniques to the solution of differential equations , reformulated Maxwell's field equations in terms of electric and...

.

It is the cumulative distribution function

Cumulative distribution function

In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...

of a random variable

Random variable

In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...

which is almost surely

Almost surely

In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...

0. (See constant random variable.)

The Heaviside function is the integral

Integral

Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...

of the Dirac delta function

Dirac delta function

: H′ = δ. This is sometimes written as

although this expansion may not hold (or even make sense) for x = 0, depending on which formalism one uses to give meaning to integrals involving δ.

Discrete form

An alternative form of the unit step, as a function of a discrete variable n:

where n is an integer

Integer

The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...

. Unlike the usual (not discrete) case, the definition of H[0] is significant.

The discrete-time unit impulse is the first difference of the discrete-time step

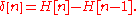
This function is the cumulative summation of the Kronecker delta:

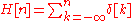
where

is the discrete unit impulse function.

Analytic approximations

For a smooth

Smooth function

In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...

approximation to the step function, one can use the logistic function

Logistic function

A logistic function or logistic curve is a common sigmoid curve, given its name in 1844 or 1845 by Pierre François Verhulst who studied it in relation to population growth. It can model the "S-shaped" curve of growth of some population P...

where a larger k corresponds to a sharper transition at x = 0. If we take H(0) = ½, equality holds in the limit:

There are many other smooth, analytic approximations to the step function. Among the possibilities are:

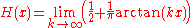
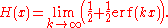
These limits hold pointwise

Pointwise

In mathematics, the qualifier pointwise is used to indicate that a certain property is defined by considering each value f of some function f. An important class of pointwise concepts are the pointwise operations — operations defined on functions by applying the operations to function values...

and in the sense of distributions

Distribution (mathematics)

. In general, however, pointwise convergence need not imply distributional convergence, and vice-versa distributional convergence need not imply pointwise convergence.

In general, any cumulative distribution function

Cumulative distribution function

(c.d.f.) of a continuous probability distribution

Probability distribution

In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....

that is peaked around zero and has a parameter that controls for variance

Variance

In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...

can serve as an approximation, in the limit as the variance approaches zero. For example, all three of the above approximations are c.d.f.s of common probability distributions: The logistic, Cauchy

Cauchy distribution

The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...

and normal distributions, respectively.

Integral representations

Often an integral representation of the Heaviside step function is useful: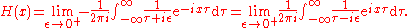

Zero argument

Since H is usually used in integration, and the value of a function at a single point does not affect its integral, it rarely matters what particular value is chosen of H(0). Indeed when H is considered as a distribution

Distribution (mathematics)

or an element of

(see Lp space

Lp space

In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...

) it does not even make sense to talk of a value at zero, since such objects are only defined almost everywhere

Almost everywhere

In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...

. If using some analytic approximation (as in the examples above) then often whatever happens to be the relevant limit at zero is used.

There exist, however, reasons for choosing a particular value.

H(0) = ½ is often used since the graph
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...

then has rotational symmetry; put another way, H-½ is then an odd function. In this case the following relation with the sign function
Sign function
In mathematics, the sign function is an odd mathematical function that extracts the sign of a real number. To avoid confusion with the sine function, this function is often called the signum function ....

holds for all x: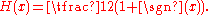
H(0) = 1 is used when H needs to be right-continuous. For instance cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...

s are usually taken to be right continuous, as are functions integrated against in Lebesgue–Stieltjes integration. In this case H is the indicator function of a closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...

semi-infinite interval: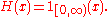
H(0) = 0 is used when H needs to be left-continuous. In this case H is an indicator function of an open
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...

semi-infinite interval:

Antiderivative and derivative

The ramp function

Ramp function

The ramp function is an elementary unary real function, easily computable as the mean of its independent variable and its absolute value.This function is applied in engineering...

is the antiderivative

Antiderivative

In calculus, an "anti-derivative", antiderivative, primitive integral or indefinite integralof a function f is a function F whose derivative is equal to f, i.e., F ′ = f...

of the Heaviside step function:

The distributional derivative of the Heaviside step function is the Dirac delta function

Dirac delta function

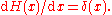
Fourier transform

The Fourier transform

Fourier transform

In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...

of the Heaviside step function is a distribution. Using one choice of constants for the definition of the Fourier transform we have

Here

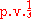is the distribution

Distribution (mathematics)

that takes a test function

to the Cauchy principal value

Cauchy principal value

In mathematics, the Cauchy principal value, named after Augustin Louis Cauchy, is a method for assigning values to certain improper integrals which would otherwise be undefined.-Formulation:...

The limit appearing in the integral is also taken in the sense of (tempered) distributions.

Algebraic representation

is a decimal number with no more than

decimal digits, the Heaviside step function can be represented by means of the following algebraic expression: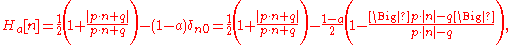

where

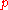and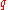

are arbitrary integers that satisfy

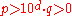, and

is a Kronecker delta function.

For instance, if

is integer, the simplest choice is:

. On the other hand, if

belongs to a set of decimal numbers with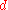

decimal digits, the simplest choice is:

Hyperfunction representation

This can be represented as a hyperfunction

Hyperfunction

In mathematics, hyperfunctions are generalizations of functions, as a 'jump' from one holomorphic function to another at a boundary, and can be thought of informally as distributions of infinite order...

Discrete form

Analytic approximations

Integral representations

Zero argument

Antiderivative and derivative

Fourier transform

Algebraic representation

Hyperfunction representation

See also