Ramond-Ramond field
Encyclopedia
In theoretical physics
, Ramond–Ramond fields are differential form
fields in the 10-dimensional spacetime
of type II supergravity
theories, which are the classical limits of type II
string theory
. The ranks of the fields depend on which type II theory is considered. As Joe Polchinski argued in 1995, D-brane
s are the charged objects that act as sources for these fields, according to the rules of p-form electrodynamics. It has been conjectured that quantum RR fields are not differential forms, but instead are classified by twisted K-theory
.
The adjective "Ramond–Ramond" reflects the fact that in the RNS formalism
, these fields appear in the Ramond–Ramond sector in which all vector fermions are periodic. Both uses of the word "Ramond" refer to Pierre Ramond
, who studied such boundary conditions and the fields that satisfy them in 1971.
and its generalization, p-form electrodynamics, Ramond–Ramond (RR) fields come in pairs consisting of a p-form
potential Cp and a (p + 1)-form field strength
Gp+1. The field strength is, as usual defined to be the exterior derivative of the potential Gp+1 = dCp.
As is usual in such theories, if one allows topologically nontrivial configurations or charged matter (D-branes) then the connections are only defined on each coordinate patch of spacetime, and the values on various patches are glued using transition functions which are gauge transformations. Unlike the case of electromagnetism, in the presence of a nontrivial Neveu–Schwarz 3-form field strength the field strength defined above is no longer gauge invariant and so also needs to be defined patchwise with the Dirac string off of a given patch interpreted itself as a D-brane. This extra complication is responsible for some of the more interesting phenomena in string theory, such as the Hanany–Witten transition.
The choices of allowed values of p depend on the theory. In type IIA supergravity, fields exist for p = 1 and p = 3. In type IIB supergravity, on the other hand, there are fields for p = 0, p = 2 and p = 4, although the p = 4 field is constrained to satisfy the self-duality condition G5 = *G5 where * is the Hodge star. The self-duality condition cannot be imposed by a Lagrangian without either introducing extra fields or ruining the manifest superPoincare invariance of the theory, thus type IIB supergravity is considered to be a non-Lagrangian theory. A third theory, called massive or Romans IIA supergravity, includes a field strength G0, called the Romans mass. Being a zero-form, it has no corresponding connection. Furthermore, the equations of motion impose that the Romans mass is constant. In the quantum theory Joseph Polchinski
has shown that G0 is an integer, which jumps by one as one crosses a D8-brane
.
in p-Brane Democracy. In D-brane Wess-Zumino Actions, T-duality and the Cosmological Constant Michael Green
, Christopher Hull and Paul Townsend
constructed the field strengths and found the gauge transformations that leave them invariant. Finally in New Formulations of D=10 Supersymmetry and D8-O8 Domain Walls the authors completed the formulation, providing a Lagrangian and explaining the role of the fermions. In this formulation one includes all of the even field strengths in IIA and all of the odd field strengths in IIB. The additional field strengths are defined by the star condition Gp=*G10-p. As a consistency check, notice that the star condition is compatible with the self-duality of G5, thus the democratic formulation contains the same number of degrees of freedom as the original formulation. Similarly to attempts to simultaneously include both electric and magnetic potentials in electromagnetism, the dual gauge potentials may not be added to the democratically-formulated Lagrangian in a way that maintains the manifest locality of the theory. This is because the dual potentials are obtained from the original potentials by integrating the star condition.
, such as diffeomorphism
s and local supersymmetry
transformations. In addition the various form-fields transform under Neveu–Schwarz and Ramond–Ramond gauge transformations.
In the democratic formulation the Ramond–Ramond gauge transformations of the gauge potentials that leave the action invariant are
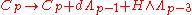
where H is the Neveu-Schwarz 3-form field strength and the gauge parameters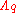
are q-forms. As the gauge transformations mix various 
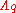's, it is necessary that each RR form be transformed simultaneously, using the same set of gauge parameters. The H-dependent terms, which have no analogue in electro-magnetism, are required to preserve the contribution to the action of the Chern-Simons terms that are present in type II supergravity theories.
Notice that there are multiple gauge parameters corresponding to the same gauge transformation, in particular we may add any (d + H)-closed form to Lambda. Thus in the quantum theory we must also gauge the gauge transformations, and then gauge those, on so on until the dimensions are sufficiently low. In the Fadeev–PPopov quantization this corresponds to adding a tower of ghosts. Mathematically, in the case in which H vanishes, the resulting structure is the Deligne cohomology
of the spacetime. For nontrivial H, after including the Dirac quantization condition, it has been conjectured to correspond instead to differential K-theory.
Notice that, thanks to the H terms in the gauge transformations, the field strengths also transform nontrivially
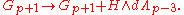
that are gauge-invariant.
Although they are gauge-invariant, the improved field strengths are neither closed nor quantized, instead they are only twisted-closed. This means that they satisfy the equation of motion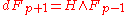
, which is just the Bianchi identity 
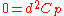. They are also "twisted-quantized" in the sense that one can transform back to the original field strength whose integrals over compact cycles are quantized. It is the original field strengths that are sourced by D-brane charge, in the sense that the integral of the original p-form field strength Gp over any contractible p-cycle is equal to the D(8-p)-brane charge linked by that cycle.
Since D-brane charge is quantized, Gp, and not the improved field strength, is quantized.
s and Bianchi identities. The former express the condition that variations of the action with respect to the various fields must be trivial. We will now restrict our attention to those field equations that come from the variation of the Ramond-Ramond (RR) fields, but in practice these need to be supplemented with the field equations coming from the variations of the Neveu-Schwarz B-field
, the graviton, the dilaton
and their superpartners the gravitinos and the dilatino.
In the democratic formulation, the Bianchi identity for the field strength Gp+1 is the classical field equation for its Hodge dual G9-p, and so it will suffice to impose the Bianchi identities for each RR field. These are just the conditions that the RR potentials Cp are locally defined, and that therefore the exterior derivative acting on them is nilpotent
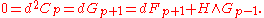
one may add sources by including a coupling Cp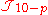
of the p-form potential to a (10-p)-form current 
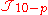in the Lagrangian
density. The usual convention in the string theory literature appears to be to not write this term explicitly in the action.
The current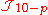
modifies the equation of motion that comes from the variation of Cp. As is the case with magnetic monopole
s in electromagnetism, this source also invaliditates the dual Bianchi identity as it is a point at which the dual field is not defined. In the modified equation of motion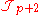
appears on the left hand side of the equation of motion instead of zero. For future simplicity, we will also interchange p and 7 − p, then the equation of motion in the presence of a source is
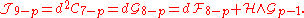
The (9-p)-form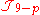
is the Dp-brane current, which means that it is Poincare dual
to the worldvolume of a (p + 1)-dimensional extended object called a Dp-brane. The discrepancy of one in the naming scheme is historical and comes from the fact that one of the p + 1 directions spanned by the Dp-brane is often timelike, leaving p spatial directions.
The above Bianchi identity is interpreted to mean that the Dp-brane is, in analogy with magnetic monopole
s in electromagnetism, magnetically charged under the RR p-form C7−p. If instead one considers this Bianchi identity to be a field equation for Cp+1, then one says that the Dp-brane is electrically charged under the (p + 1)-form Cp+1.
The above equation of motion implies that there are two ways to derive the Dp-brane charge from the ambient fluxes. First, one may integrate dG8-p over a surface, which will give the Dp-brane charge intersected by that surface. The second method is related to the first by Stokes' theorem
. One may integrate G8-p over a cycle, this will yield the Dp-brane charge linked by that cycle. The quantization of Dp-brane charge in the quantum theory then implies the quantization of the field strengths G, but not of the improved field strengths F.
Twisted K-theory
It has been conjectured that RR fields, as well as D-branes, are classified by twisted K-theory
. In this framework, the above equations of motion have natural interpretations. The source free equations of motion for the improved field strengths F imply that the formal sum of all of the Fp's is an element of the H-twisted de Rham cohomology
. This is a version of De Rham cohomology in which the differential is not the exterior derivative d, but instead (d+H) where H is the Neveu-Schwarz 3-form. Notice that (d+H), as is necessary for the cohomology to be well-defined, squares to zero.
The improved field strengths F live in the classical theory, where the transition from quantum to classical is interpreted as tensoring by the rationals. So the F's must be some rational version of twisted K-theory. Such a rational version, in fact a characteristic class of twisted K-theory, is already known. It is the twisted Chern class defined in Twisted K-theory and the K-theory of Bundle Gerbes by Peter Bouwknegt, Alan L. Carey, Varghese Mathai
, Michael K. Murray and Danny Stevenson and extended in Chern character in twisted K-Theory: Equivariant and holomorphic cases. The authors have shown that twisted Chern characters are always elements of the H-twisted de Rham cohomology.
Unlike the improved field strengths, the original field strengths G's are untwisted, integral cohomology classes. In addition the G's are not gauge-invariant, which means that they are not uniquely defined but instead may only be defined as equivalence classes. These correspond to the cohomology classes in the Atiyah Hirzebruch Spectral Sequence construction of twisted K-theory, which are only defined up to terms which are closed under any of a series of differential operator
s.
The source terms appear to be obstructions to the existence of a K-theory class. The other equations of motion, such as those obtained by varying the NS B-field, do not have K-theory interpretations. The incorporation of these corrections in the K-theory framework is an open problem. For more on this problem, click here.
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, Ramond–Ramond fields are differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
fields in the 10-dimensional spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
of type II supergravity
Supergravity
In theoretical physics, supergravity is a field theory that combines the principles of supersymmetry and general relativity. Together, these imply that, in supergravity, the supersymmetry is a local symmetry...
theories, which are the classical limits of type II
Type II string theory
In theoretical physics, type II string theory is a unified term that includes both type IIA strings and type IIB strings. These account for two of the five consistent superstring theories in ten dimensions. Both theories have the maximal amount of supersymmetry — namely 32 supercharges...
string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
. The ranks of the fields depend on which type II theory is considered. As Joe Polchinski argued in 1995, D-brane
D-brane
In string theory, D-branes are a class of extended objects upon which open strings can end with Dirichlet boundary conditions, after which they are named. D-branes were discovered by Dai, Leigh and Polchinski, and independently by Hořava in 1989...
s are the charged objects that act as sources for these fields, according to the rules of p-form electrodynamics. It has been conjectured that quantum RR fields are not differential forms, but instead are classified by twisted K-theory
K-theory (physics)
In string theory, the K-theory classification refers to a conjectured application of K-theory to superstrings, to classify the allowed Ramond-Ramond field strengths as well as the charges of stable D-branes....
.
The adjective "Ramond–Ramond" reflects the fact that in the RNS formalism
RNS formalism
In theoretical physics, the RNS formalism or Ramond-Neveu-Schwarz formalism is a particular method to describe the degrees of freedom of a string in superstring theory in which the elementary fields on the worldsheet are the bosonic scalar fields describing the embedding of the string in spacetime,...
, these fields appear in the Ramond–Ramond sector in which all vector fermions are periodic. Both uses of the word "Ramond" refer to Pierre Ramond
Pierre Ramond
Pierre Ramond is a Distinguished Professor of Physics at University of Florida in Gainesville, Florida...
, who studied such boundary conditions and the fields that satisfy them in 1971.
The fields in each theory
As in Maxwell's theory of electromagnetismClassical electromagnetism
Classical electromagnetism is a branch of theoretical physics that studies consequences of the electromagnetic forces between electric charges and currents...
and its generalization, p-form electrodynamics, Ramond–Ramond (RR) fields come in pairs consisting of a p-form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
potential Cp and a (p + 1)-form field strength
Field strength
In physics, the field strength of a field is the magnitude of its vector value.In theoretical physics, field strength is another name for the curvature form...
Gp+1. The field strength is, as usual defined to be the exterior derivative of the potential Gp+1 = dCp.
As is usual in such theories, if one allows topologically nontrivial configurations or charged matter (D-branes) then the connections are only defined on each coordinate patch of spacetime, and the values on various patches are glued using transition functions which are gauge transformations. Unlike the case of electromagnetism, in the presence of a nontrivial Neveu–Schwarz 3-form field strength the field strength defined above is no longer gauge invariant and so also needs to be defined patchwise with the Dirac string off of a given patch interpreted itself as a D-brane. This extra complication is responsible for some of the more interesting phenomena in string theory, such as the Hanany–Witten transition.
The choices of allowed values of p depend on the theory. In type IIA supergravity, fields exist for p = 1 and p = 3. In type IIB supergravity, on the other hand, there are fields for p = 0, p = 2 and p = 4, although the p = 4 field is constrained to satisfy the self-duality condition G5 = *G5 where * is the Hodge star. The self-duality condition cannot be imposed by a Lagrangian without either introducing extra fields or ruining the manifest superPoincare invariance of the theory, thus type IIB supergravity is considered to be a non-Lagrangian theory. A third theory, called massive or Romans IIA supergravity, includes a field strength G0, called the Romans mass. Being a zero-form, it has no corresponding connection. Furthermore, the equations of motion impose that the Romans mass is constant. In the quantum theory Joseph Polchinski
Joseph Polchinski
Joseph Polchinski is a physicist working on string theory. He graduated from Canyon del Oro High School in Tucson, Arizona in 1971, obtained his B.S. degree from Caltech in 1975, and his Ph.D. from the University of California, Berkeley in 1980 under the supervision of Stanley Mandelstam...
has shown that G0 is an integer, which jumps by one as one crosses a D8-brane
D-brane
In string theory, D-branes are a class of extended objects upon which open strings can end with Dirichlet boundary conditions, after which they are named. D-branes were discovered by Dai, Leigh and Polchinski, and independently by Hořava in 1989...
.
The democratic formulation
It is often convenient to use the democratic formulation of type II string theories, which was introduced by Paul TownsendPaul Townsend
Paul Kingsley Townsend FRS is a British physicist, currently a Professor of Theoretical Physics in Cambridge University's Department of Applied Mathematics and Theoretical Physics. He is notable for his work on string theory....
in p-Brane Democracy. In D-brane Wess-Zumino Actions, T-duality and the Cosmological Constant Michael Green
Michael Green (physicist)
Michael Boris Green FRS is a British physicist and one of the pioneers of string theory. Currently a professor in the Department of Applied Mathematics and Theoretical Physics and a Fellow in Clare Hall at the University of Cambridge in England, he succeeded Stephen Hawking on 1 November 2009...
, Christopher Hull and Paul Townsend
Paul Townsend
Paul Kingsley Townsend FRS is a British physicist, currently a Professor of Theoretical Physics in Cambridge University's Department of Applied Mathematics and Theoretical Physics. He is notable for his work on string theory....
constructed the field strengths and found the gauge transformations that leave them invariant. Finally in New Formulations of D=10 Supersymmetry and D8-O8 Domain Walls the authors completed the formulation, providing a Lagrangian and explaining the role of the fermions. In this formulation one includes all of the even field strengths in IIA and all of the odd field strengths in IIB. The additional field strengths are defined by the star condition Gp=*G10-p. As a consistency check, notice that the star condition is compatible with the self-duality of G5, thus the democratic formulation contains the same number of degrees of freedom as the original formulation. Similarly to attempts to simultaneously include both electric and magnetic potentials in electromagnetism, the dual gauge potentials may not be added to the democratically-formulated Lagrangian in a way that maintains the manifest locality of the theory. This is because the dual potentials are obtained from the original potentials by integrating the star condition.
Ramond–Ramond gauge transformations
The type II supergravity Langragians are invariant under a number of local symmetriesLocal symmetry
In physics, a local symmetry is symmetry of some physical quantity, which smoothly depends on the point of the base manifold. Such quantities can be for example an observable, a tensor or the Lagrangian of a theory....
, such as diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
s and local supersymmetry
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
transformations. In addition the various form-fields transform under Neveu–Schwarz and Ramond–Ramond gauge transformations.
In the democratic formulation the Ramond–Ramond gauge transformations of the gauge potentials that leave the action invariant are
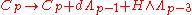
where H is the Neveu-Schwarz 3-form field strength and the gauge parameters
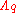are q-forms. As the gauge transformations mix various 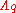's, it is necessary that each RR form be transformed simultaneously, using the same set of gauge parameters. The H-dependent terms, which have no analogue in electro-magnetism, are required to preserve the contribution to the action of the Chern-Simons terms that are present in type II supergravity theories.Notice that there are multiple gauge parameters corresponding to the same gauge transformation, in particular we may add any (d + H)-closed form to Lambda. Thus in the quantum theory we must also gauge the gauge transformations, and then gauge those, on so on until the dimensions are sufficiently low. In the Fadeev–PPopov quantization this corresponds to adding a tower of ghosts. Mathematically, in the case in which H vanishes, the resulting structure is the Deligne cohomology
Deligne cohomology
In mathematics, Deligne cohomology is the hypercohomology of the Deligne complex of a complex manifold. It was introduced by Pierre Deligne in unpublished work in about 1972 as a cohomology theory for algebraic varieties that includes both ordinary cohomology and intermediate Jacobians.For...
of the spacetime. For nontrivial H, after including the Dirac quantization condition, it has been conjectured to correspond instead to differential K-theory.
Notice that, thanks to the H terms in the gauge transformations, the field strengths also transform nontrivially
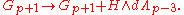
The improved field strengths
One often introduces improved field strengthsthat are gauge-invariant.
Although they are gauge-invariant, the improved field strengths are neither closed nor quantized, instead they are only twisted-closed. This means that they satisfy the equation of motion
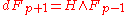, which is just the Bianchi identity 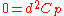. They are also "twisted-quantized" in the sense that one can transform back to the original field strength whose integrals over compact cycles are quantized. It is the original field strengths that are sourced by D-brane charge, in the sense that the integral of the original p-form field strength Gp over any contractible p-cycle is equal to the D(8-p)-brane charge linked by that cycle.Since D-brane charge is quantized, Gp, and not the improved field strength, is quantized.
Equations and Bianchi identities
As usual in p-form gauge theories, the form fields must obey the classical field equationField equation
A field equation is an equation in a physical theory that describes how a fundamental force interacts with matter...
s and Bianchi identities. The former express the condition that variations of the action with respect to the various fields must be trivial. We will now restrict our attention to those field equations that come from the variation of the Ramond-Ramond (RR) fields, but in practice these need to be supplemented with the field equations coming from the variations of the Neveu-Schwarz B-field
Kalb-Ramond field
In theoretical physics in general and string theory in particular, the Kalb–Ramond field, also known as the NS-NS B-field, is a quantum field that transforms as a two-form i.e. an antisymmetric tensor field with two indices....
, the graviton, the dilaton
Dilaton
In particle physics, a dilaton is a hypothetical particle. It also appears in Kaluza-Klein theory's compactifications of extra dimensions when the volume of the compactified dimensions vary....
and their superpartners the gravitinos and the dilatino.
In the democratic formulation, the Bianchi identity for the field strength Gp+1 is the classical field equation for its Hodge dual G9-p, and so it will suffice to impose the Bianchi identities for each RR field. These are just the conditions that the RR potentials Cp are locally defined, and that therefore the exterior derivative acting on them is nilpotent
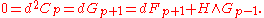
D-branes are sources for RR fields
In many applications one wishes to add sources for the RR fields. These sources are called D-branes. As in classical electromagnetismClassical electromagnetism
Classical electromagnetism is a branch of theoretical physics that studies consequences of the electromagnetic forces between electric charges and currents...
one may add sources by including a coupling Cp
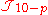of the p-form potential to a (10-p)-form current 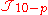in the LagrangianLagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
density. The usual convention in the string theory literature appears to be to not write this term explicitly in the action.
The current
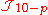modifies the equation of motion that comes from the variation of Cp. As is the case with magnetic monopoleMagnetic monopole
A magnetic monopole is a hypothetical particle in particle physics that is a magnet with only one magnetic pole . In more technical terms, a magnetic monopole would have a net "magnetic charge". Modern interest in the concept stems from particle theories, notably the grand unified and superstring...
s in electromagnetism, this source also invaliditates the dual Bianchi identity as it is a point at which the dual field is not defined. In the modified equation of motion
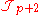appears on the left hand side of the equation of motion instead of zero. For future simplicity, we will also interchange p and 7 − p, then the equation of motion in the presence of a source is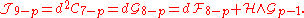The (9-p)-form
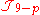is the Dp-brane current, which means that it is Poincare dualPoincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
to the worldvolume of a (p + 1)-dimensional extended object called a Dp-brane. The discrepancy of one in the naming scheme is historical and comes from the fact that one of the p + 1 directions spanned by the Dp-brane is often timelike, leaving p spatial directions.
The above Bianchi identity is interpreted to mean that the Dp-brane is, in analogy with magnetic monopole
Magnetic monopole
A magnetic monopole is a hypothetical particle in particle physics that is a magnet with only one magnetic pole . In more technical terms, a magnetic monopole would have a net "magnetic charge". Modern interest in the concept stems from particle theories, notably the grand unified and superstring...
s in electromagnetism, magnetically charged under the RR p-form C7−p. If instead one considers this Bianchi identity to be a field equation for Cp+1, then one says that the Dp-brane is electrically charged under the (p + 1)-form Cp+1.
The above equation of motion implies that there are two ways to derive the Dp-brane charge from the ambient fluxes. First, one may integrate dG8-p over a surface, which will give the Dp-brane charge intersected by that surface. The second method is related to the first by Stokes' theorem
Stokes' theorem
In differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
. One may integrate G8-p over a cycle, this will yield the Dp-brane charge linked by that cycle. The quantization of Dp-brane charge in the quantum theory then implies the quantization of the field strengths G, but not of the improved field strengths F.
Twisted K-theoryTwisted K-theoryIn mathematics, twisted K-theory is a variation on K-theory, a mathematical theory from the 1950s that spans algebraic topology, abstract algebra and operator theory....
interpretation
It has been conjectured that RR fields, as well as D-branes, are classified by twisted K-theoryK-theory (physics)
In string theory, the K-theory classification refers to a conjectured application of K-theory to superstrings, to classify the allowed Ramond-Ramond field strengths as well as the charges of stable D-branes....
. In this framework, the above equations of motion have natural interpretations. The source free equations of motion for the improved field strengths F imply that the formal sum of all of the Fp's is an element of the H-twisted de Rham cohomology
De Rham cohomology
In mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
. This is a version of De Rham cohomology in which the differential is not the exterior derivative d, but instead (d+H) where H is the Neveu-Schwarz 3-form. Notice that (d+H), as is necessary for the cohomology to be well-defined, squares to zero.
The improved field strengths F live in the classical theory, where the transition from quantum to classical is interpreted as tensoring by the rationals. So the F's must be some rational version of twisted K-theory. Such a rational version, in fact a characteristic class of twisted K-theory, is already known. It is the twisted Chern class defined in Twisted K-theory and the K-theory of Bundle Gerbes by Peter Bouwknegt, Alan L. Carey, Varghese Mathai
Mathai Varghese
Mathai Varghese is a mathematician and an Australian Research Council Australian Professorial Fellow at the University of Adelaide. His most influential contribution to date is the Mathai-Quillen formalism, which he formulated together with Daniel Quillen, and which has since found applications in...
, Michael K. Murray and Danny Stevenson and extended in Chern character in twisted K-Theory: Equivariant and holomorphic cases. The authors have shown that twisted Chern characters are always elements of the H-twisted de Rham cohomology.
Unlike the improved field strengths, the original field strengths G's are untwisted, integral cohomology classes. In addition the G's are not gauge-invariant, which means that they are not uniquely defined but instead may only be defined as equivalence classes. These correspond to the cohomology classes in the Atiyah Hirzebruch Spectral Sequence construction of twisted K-theory, which are only defined up to terms which are closed under any of a series of differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
s.
The source terms appear to be obstructions to the existence of a K-theory class. The other equations of motion, such as those obtained by varying the NS B-field, do not have K-theory interpretations. The incorporation of these corrections in the K-theory framework is an open problem. For more on this problem, click here.