
Field equation
Encyclopedia
A field equation is an equation in a physical theory that describes how a fundamental force (or a combination of such forces) interacts with matter
. The four fundamental forces are gravitation
, electromagnetism
, strong interaction
and weak interaction
.
Before the theory of quantum mechanics
was fully developed, there were two known field theories, namely gravitation
and electromagnetism
(these two are sometimes referred to as classical field theories, as they were formulated before the advent of quantum mechanics, and hence do not take into account quantum phenomena).
Modern field equations tend to be tensor equations.
The gravitational field at the point r due to several masses, Mi, located at points, ri, is given by

where Gc is Newton's gravitational constant
. Note that the direction of the field points from the position, r, to the position of the masses, ri; this is ensured by the minus sign. In a nutshell, this means all masses attract.
:

To understand where this equation comes from, we need to examine the form and source of the force fields. We recognise that charges are the sources and sinks of electrostatic fields: positive charges emanate electric field lines, and field lines terminate at negative charges. Similarly, in Newton's gravitation masses are the sources of the field so that field lines terminate at objects that have mass. Formalised Gauss' Law for electric fields (using the more general divergence theorem
):
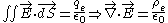
and for masses
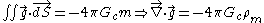
where ρe and ρm represents the charge and mass densities respectively. Incidentally, this similarity arises from the similarity of the form of Newton's law of gravitation and Coulomb's law
.
Since the force fields are related to their potentials by the gradient:
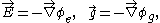
we can substitute the potential for the field to get Poisson's equation
:
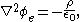

:
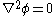
This works by finding a Lorentz scalar, the Lagrangian density, from which the field equations and symmetries can be readily derived.
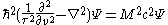
This is the familiar Klein–Gordon equation in the four dimensions of space and velocity.
are Maxwell's equations which describe how electromagnetic fields are produced from charged particles and are written in the framework of special relativity
(which was devised to consistently describe electromagnetism and classical mechanics
) as:
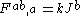
This arises from the following Lagrangian
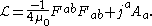
, in which gravitation
is thought of as being due to a curved spacetime
, caused by masses. The Einstein field equation - which describes how this curvature is produced by masses - is:

The vacuum solution can be obtained by varying the following action with respect to the metric
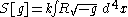
s.
Matter
Matter is a general term for the substance of which all physical objects consist. Typically, matter includes atoms and other particles which have mass. A common way of defining matter is as anything that has mass and occupies volume...
. The four fundamental forces are gravitation
Gravitation
Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...
, electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
, strong interaction
Strong interaction
In particle physics, the strong interaction is one of the four fundamental interactions of nature, the others being electromagnetism, the weak interaction and gravitation. As with the other fundamental interactions, it is a non-contact force...
and weak interaction
Weak interaction
Weak interaction , is one of the four fundamental forces of nature, alongside the strong nuclear force, electromagnetism, and gravity. It is responsible for the radioactive decay of subatomic particles and initiates the process known as hydrogen fusion in stars...
.
Before the theory of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
was fully developed, there were two known field theories, namely gravitation
Gravitation
Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...
and electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
(these two are sometimes referred to as classical field theories, as they were formulated before the advent of quantum mechanics, and hence do not take into account quantum phenomena).
Modern field equations tend to be tensor equations.
Newton's theory of universal gravitation
The first field theory of gravity was Newton's theory of gravitation, which described gravity as obeying an inverse square law. This was very useful in describing the motion of planets around the Sun.The gravitational field at the point r due to several masses, Mi, located at points, ri, is given by

where Gc is Newton's gravitational constant
Gravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
. Note that the direction of the field points from the position, r, to the position of the masses, ri; this is ensured by the minus sign. In a nutshell, this means all masses attract.
Poisson's equation
The term "potential theory" arises from the fact that, in 19th century physics, the fundamental forces of nature were believed to be derived from potentials which satisfied Laplace's equation. Poisson addressed the question of the stability of the planetary orbits, which had already been settled by Lagrange to the first degree of approximation for the disturbing forces and created Poisson's equationPoisson's equation
In mathematics, Poisson's equation is a partial differential equation of elliptic type with broad utility in electrostatics, mechanical engineering and theoretical physics...
:

To understand where this equation comes from, we need to examine the form and source of the force fields. We recognise that charges are the sources and sinks of electrostatic fields: positive charges emanate electric field lines, and field lines terminate at negative charges. Similarly, in Newton's gravitation masses are the sources of the field so that field lines terminate at objects that have mass. Formalised Gauss' Law for electric fields (using the more general divergence theorem
Divergence theorem
In vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem...
):
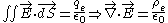
and for masses
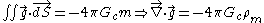
where ρe and ρm represents the charge and mass densities respectively. Incidentally, this similarity arises from the similarity of the form of Newton's law of gravitation and Coulomb's law
Coulomb's law
Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
.
Since the force fields are related to their potentials by the gradient:
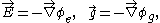
we can substitute the potential for the field to get Poisson's equation
Poisson's equation
In mathematics, Poisson's equation is a partial differential equation of elliptic type with broad utility in electrostatics, mechanical engineering and theoretical physics...
:
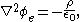

Laplace's equation
In the case where there is no source term (e.g. vacuum, or paired charges), these potentials obey Laplace's equationLaplace's equation
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
:
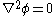
Relativistic fields
When it was realised that Lorentz invariance is an essential feature of nature, it became desirable to model everything as a relativistic field. This could be conveniently done under the formalism of relativistic (or covariant) classical field theory.This works by finding a Lorentz scalar, the Lagrangian density, from which the field equations and symmetries can be readily derived.
A scalar particle with non-zero mass
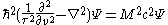
This is the familiar Klein–Gordon equation in the four dimensions of space and velocity.
Maxwell's equations
The electromagnetic force is best described by Maxwell's theory of electromagnetism. The field equations of classical electromagnetismClassical electromagnetism
Classical electromagnetism is a branch of theoretical physics that studies consequences of the electromagnetic forces between electric charges and currents...
are Maxwell's equations which describe how electromagnetic fields are produced from charged particles and are written in the framework of special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
(which was devised to consistently describe electromagnetism and classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
) as:
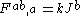
This arises from the following Lagrangian
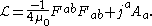
Einstein's field equation
Newtonian gravitation is now superseded by Einstein's theory of general relativityGeneral relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, in which gravitation
Gravitation
Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...
is thought of as being due to a curved spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
, caused by masses. The Einstein field equation - which describes how this curvature is produced by masses - is:

The vacuum solution can be obtained by varying the following action with respect to the metric
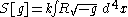
Vacuum field equations
Vacuum field equations are the field equations written without matter (including sources). Solutions of the vacuum field equations are called vacuum solutionVacuum solution
A vacuum solution is a solution of a field equation in which the sources of the field are taken to be identically zero. That is, such field equations are written without matter interaction .-Examples:...
s.

