
Photon polarization
Encyclopedia
Photon polarization is the quantum mechanical
description of the classical
polarized sinusoidal plane
electromagnetic wave. Individual photon
s are completely polarized. Their polarization state can be linear
or circular
, or it can be elliptical
, which is anywhere in between of linear and circular polarization.
The description contains many of the physical concepts and much of the mathematical machinery of more involved quantum descriptions, such as the quantum mechanics of an electron in a potential well
, and forms a fundamental basis for an understanding of more complicated quantum phenomena.
Much of the mathematical machinery of quantum mechanics, such as state vectors, probability amplitude
s, unitary operator
s, and Hermitian operators, emerge naturally from the classical Maxwell's equations
in the description.
The quantum polarization state vector for the photon, for instance, is identical with the Jones vector, usually used to describe the polarization of a classical wave
.
Unitary operators emerge from the classical requirement of the conservation of energy
of a classical wave propagating through media that alter the polarization state of the wave. Hermitian operators then follow for infinitesimal transformations of a classical polarization state.
Many of the implications of the mathematical machinery are easily verified experimentally. In fact, many of the experiments can be performed with two pairs (or one broken pair) of polaroid sunglasses.
The connection with quantum mechanics is made through the identification of a minimum packet size, called a photon
, for energy in the electromagnetic field. The identification is based on the theories of Planck
and the interpretation of those theories by Einstein
. The correspondence principle
then allows the identification of momentum and angular momentum (called spin
), as well as energy, with the photon.

where the angle describes the relation between the amplitude
describes the relation between the amplitude
s of the electric field components in the x and y directions, and and
and  are the phase angles of the electric field components in the x and y directions respectively.
are the phase angles of the electric field components in the x and y directions respectively.

and

This implies


where is the amplitude of the wave polarized in the x direction and
is the amplitude of the wave polarized in the x direction and  is the amplitude of the wave polarized in the y direction.
is the amplitude of the wave polarized in the y direction.
The angles and
and  characterize the phase relationship between the wave polarized in x and the wave polarized in y.
characterize the phase relationship between the wave polarized in x and the wave polarized in y.
The Jones vector contains all the polarization information for a plane wave. If the Jones vector for a sinusoidal plane wave, the amplitude , and the dispersion relationship
, and the dispersion relationship

are known, then the state of the wave is completely characterized.
Here is the angular frequency
is the angular frequency
of the wave, and is the speed of light
is the speed of light
.
The notation for the Jones vector is the bra-ket notation
of Dirac
, which is normally used in a quantum context. The quantum notation is used here in anticipation of the interpretation of the Jones vector as a quantum state vector.
given by


 The wave is linearly polarized (or plane polarized) when the phase angles
The wave is linearly polarized (or plane polarized) when the phase angles  are equal,
are equal,

This represents a wave with phase
 polarized at an angle
polarized at an angle  with respect to the x axis. In that case the Jones vector can be written
with respect to the x axis. In that case the Jones vector can be written

The state vectors for linear polarization in x or y are special cases of this state vector.
If unit vectors are defined such that

and

then the linearly polarized polarization state can written in the "x-y basis" as

 and
and  differs by exactly
differs by exactly  and the x amplitude equals the y amplitude the wave is circularly polarized
and the x amplitude equals the y amplitude the wave is circularly polarized
. The Jones vector then becomes

where the plus sign indicates right circular polarization and the minus sign indicates left circular polarization. In the case of circular polarization, the electric field vector of constant magnitude rotates in the x-y plane.
If unit vectors are defined such that

and

then an arbitrary polarization state can written in the "R-L basis" as

where

and

We can see that

. The state vector is given by

 and then having the real parts of its components interpreted as x and y coordinates respectively. That is:
and then having the real parts of its components interpreted as x and y coordinates respectively. That is:

If only the traced out shape and the direction of the rotation of is considered when interpreting the polarization state, i.e. only

(where and are defined as above) and whether it is overall more right circularly or left circularly polarized (i.e. whether or vice versa), it can be seen that the physical interpretation will be the same even if the state is multiplied by an arbitrary phase factor, since

and the direction of rotation will remain the same. In other words, there is no physical difference between two polarization states and
and  , between which only a phase factor differs.
, between which only a phase factor differs.
It can be seen that for a linearly polarized state, M will be a line in the xy plane, with length 2 and its middle in the origin, and whose slope equals to . For a circularly polarized state, M will be a circle with radius and with the middle in the origin.
in classical electromagnetic fields is (cgs units)

For a plane wave, this becomes

where the energy has been averaged over a wavelength of the wave.

with a similar expression for the y component resulting in .
.
The fraction in both components is


For a sinusoidal plane wave traveling in the z direction, the momentum is in the z direction and is related to the energy density:

The momentum density has been averaged over a wavelength.

For a sinusoidal plane wave propagating along axis the orbital angular momentum density vanishes. The spin angular momentum density is in the
axis the orbital angular momentum density vanishes. The spin angular momentum density is in the  direction and is given by
direction and is given by

where again the density is averaged over a wavelength.
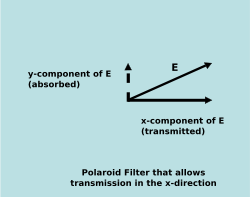 A linear filter
A linear filter
transmits one component of a plane wave and absorbs the perpendicular component. In that case, if the filter is polarized in the x direction, the fraction of energy passing through the filter is

crystal transforms the polarization state of an electromagnetic wave without loss of wave energy. Birefringent crystals therefore provide an ideal test bed for examining the conservative transformation of polarization states. Even though this treatment is still purely classical, standard quantum tools such as unitary and Hermitian operators that evolve the state in time naturally emerge.
 with respect to the optic axis, the incident state vector can be written
with respect to the optic axis, the incident state vector can be written

and the state vector for the emerging wave can be written

While the initial state was linearly polarized, the final state is elliptically polarized. The birefringent crystal alters the character of the polarization.
 The initial polarization state is transformed into the final state with the operator
The initial polarization state is transformed into the final state with the operator
U. The dual of the final state is given by

where is the adjoint
is the adjoint
of U, the complex conjugate transpose of the matrix.

In this ideal case, all the energy impinging on the crystal emerges from the crystal. An operator U with the property that

where I is the identity operator
and U is called a unitary operator
. The unitary property is necessary to ensure energy conservation
in state transformations.
 If the crystal is very thin, the final state will be only slightly different from the initial state. The unitary operator will be close to the identity operator. We can define the operator H by
If the crystal is very thin, the final state will be only slightly different from the initial state. The unitary operator will be close to the identity operator. We can define the operator H by

and the adjoint by

Energy conservation then requires

This requires that

Operators like this that are equal to their adjoints are called Hermitian
or self-adjoint.
The infinitesimal transition of the polarization state is

Thus, energy conservation requires that infinitesimal transformations of a polarization state occur through the action of a Hermitian operator.
. It is a testament, however, to the generality of Maxwell's equations
for electrodynamics that the treatment can be made quantum mechanical
with only a reinterpretation of classical quantities. The reinterpretation is based on the theories of Max Planck
and the interpretation by Albert Einstein
of those theories and of other experiments.
Einsteins's conclusion from early experiments on the photoelectric effect
is that electromagnetic radiation is composed of irreducible packets of energy, known as photon
s. The energy of each packet is related to the angular frequency of the wave by the relation

where is an experimentally determined quantity known as Planck's constant. If there are
is an experimentally determined quantity known as Planck's constant. If there are  photons in a box of volume
photons in a box of volume  , the energy in the electromagnetic field is
, the energy in the electromagnetic field is

and the energy density is

The energy of a photon can be related to classical fields through the correspondence principle
which states that for a large number of photons, the quantum and classical treatments must agree. Thus, for very large , the quantum energy density must be the same as the classical energy density
, the quantum energy density must be the same as the classical energy density

The number of photons in the box is then


which implies that the momentum of a photon is


which implies that the spin angular momentum of the photon is

the quantum interpretation of this expression is that the photon has a probability of of having a spin angular momentum of
of having a spin angular momentum of  and a probability of
and a probability of  of having a spin angular momentum of
of having a spin angular momentum of  . We can therefore think of the spin angular momentum of the photon being quantized as well as the energy. This has indeed been experimentally verified. Photons have only been observed to have spin angular momenta of
. We can therefore think of the spin angular momentum of the photon being quantized as well as the energy. This has indeed been experimentally verified. Photons have only been observed to have spin angular momenta of  .
.
The spin
of the photon is defined as the coefficient of in the spin angular momentum calculation. A photon has spin 1 if it is in the
in the spin angular momentum calculation. A photon has spin 1 if it is in the  state and -1 if it is in the
state and -1 if it is in the  state. The spin operator is defined as the outer product
state. The spin operator is defined as the outer product

The eigenvectors of the spin operator are and
and  with eigenvalues 1 and -1, respectively.
with eigenvalues 1 and -1, respectively.
The expected value of a spin measurement on a photon is then

An operator S has been associated with an observable quantity, the spin angular momentum. The eigenvalues of the operator are the allowed observable values. This has been demonstrated for spin angular momentum, but it is in general true for any observable quantity.
We can write the circularly polarized states as

where s=1 for

and s= -1 for

An arbitrary state can be written

where

When the state is written in spin notation, the spin operator can be written


The eigenvectors of the differential spin operator are

To see this note

The spin angular momentum operator is

:
contains the basic probability information. In general, the rules for combining probability amplitudes look very much like the classical rules for composition of probabilities: [The following quote is from Baym, Chapter 1]
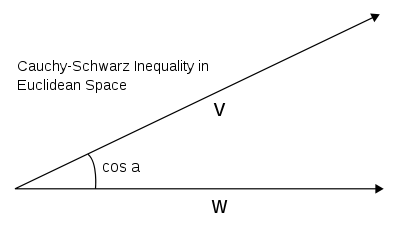
If B A ψ and A B ψ are defined then
where

is the operator mean
of observable X in the system state ψ and

Here

is called the commutator
of A and B.
This is a purely mathematical result. No reference has been made to any physical quantity or principle. It simply states that the uncertainty of an operator acting on a state times the uncertainty of another operator acting on the state is not necessarily zero.

which simply states that angular momentum and the polarization angle cannot be measured simultaneously with infinite accuracy.
s of spin states of the photon. Energy conservation requires that the states be transformed with a unitary operation. This implies that infinitesimal transformations are transformed with a Hermitian operator. These conclusions are a natural consequence of the structure of Maxwell's equations for classical waves.
Quantum mechanics enters the picture when observed quantities are measured and found to be discrete rather than continuous. The allowed observable values are determined by the eigenvalues of the operators associated with the observable. In the case angular momentum, for instance, the allowed observable values are the eigenvalues of the spin operator.
These concepts have emerged naturally from Maxwell's equations
and Planck's and Einstein's theories. They have been found to be true for many other physical systems. In fact, the typical program is to assume the concepts of this section and then to infer the unknown dynamics of a physical system. This was done, for instance, with the dynamics of electrons. In that case, working back from the principles in this section, the quantum dynamics of particles were inferred, leading to Schrödinger's equation, a departure from Newtonian mechanics. The solution of this equation for atoms led to the explanation of the Balmer series
for atomic spectra and consequently formed a basis for all of atomic physics and chemistry.
This is not the only occasion in which Maxwell's equations have forced a restructuring of Newtonian mechanics. Maxwell's equations are relativistically consistent. Special relativity
resulted from attempts to make classical mechanics consistent with Maxwell's equations (see, for example, Moving magnet and conductor problem
).
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
description of the classical
Classical physics
What "classical physics" refers to depends on the context. When discussing special relativity, it refers to the Newtonian physics which preceded relativity, i.e. the branches of physics based on principles developed before the rise of relativity and quantum mechanics...
polarized sinusoidal plane
Plane wave
In the physics of wave propagation, a plane wave is a constant-frequency wave whose wavefronts are infinite parallel planes of constant peak-to-peak amplitude normal to the phase velocity vector....
electromagnetic wave. Individual photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
s are completely polarized. Their polarization state can be linear
Linear polarization
In electrodynamics, linear polarization or plane polarization of electromagnetic radiation is a confinement of the electric field vector or magnetic field vector to a given plane along the direction of propagation...
or circular
Circular polarization
In electrodynamics, circular polarization of an electromagnetic wave is a polarization in which the electric field of the passing wave does not change strength but only changes direction in a rotary type manner....
, or it can be elliptical
Elliptical polarization
In electrodynamics, elliptical polarization is the polarization of electromagnetic radiation such that the tip of the electric field vector describes an ellipse in any fixed plane intersecting, and normal to, the direction of propagation...
, which is anywhere in between of linear and circular polarization.
The description contains many of the physical concepts and much of the mathematical machinery of more involved quantum descriptions, such as the quantum mechanics of an electron in a potential well
Potential well
A potential well is the region surrounding a local minimum of potential energy. Energy captured in a potential well is unable to convert to another type of energy because it is captured in the local minimum of a potential well...
, and forms a fundamental basis for an understanding of more complicated quantum phenomena.
Much of the mathematical machinery of quantum mechanics, such as state vectors, probability amplitude
Probability amplitude
In quantum mechanics, a probability amplitude is a complex number whose modulus squared represents a probability or probability density.For example, if the probability amplitude of a quantum state is \alpha, the probability of measuring that state is |\alpha|^2...
s, unitary operator
Unitary operator
In functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
s, and Hermitian operators, emerge naturally from the classical Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
in the description.
The quantum polarization state vector for the photon, for instance, is identical with the Jones vector, usually used to describe the polarization of a classical wave
Wave
In physics, a wave is a disturbance that travels through space and time, accompanied by the transfer of energy.Waves travel and the wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass...
.
Unitary operators emerge from the classical requirement of the conservation of energy
Conservation of energy
The nineteenth century law of conservation of energy is a law of physics. It states that the total amount of energy in an isolated system remains constant over time. The total energy is said to be conserved over time...
of a classical wave propagating through media that alter the polarization state of the wave. Hermitian operators then follow for infinitesimal transformations of a classical polarization state.
Many of the implications of the mathematical machinery are easily verified experimentally. In fact, many of the experiments can be performed with two pairs (or one broken pair) of polaroid sunglasses.
The connection with quantum mechanics is made through the identification of a minimum packet size, called a photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
, for energy in the electromagnetic field. The identification is based on the theories of Planck
Max Planck
Max Karl Ernst Ludwig Planck, ForMemRS, was a German physicist who actualized the quantum physics, initiating a revolution in natural science and philosophy. He is regarded as the founder of the quantum theory, for which he received the Nobel Prize in Physics in 1918.-Life and career:Planck came...
and the interpretation of those theories by Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
. The correspondence principle
Correspondence principle
In physics, the correspondence principle states that the behavior of systems described by the theory of quantum mechanics reproduces classical physics in the limit of large quantum numbers....
then allows the identification of momentum and angular momentum (called spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
), as well as energy, with the photon.
Polarization of classical electromagnetic waves
Jones vector
The polarization of a classical sinusoidal plane wave traveling in the z direction can be characterized by the Jones vector
where the angle
 describes the relation between the amplitude
describes the relation between the amplitudeAmplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
s of the electric field components in the x and y directions, and
 and
and  are the phase angles of the electric field components in the x and y directions respectively.
are the phase angles of the electric field components in the x and y directions respectively.
and

This implies


where
 is the amplitude of the wave polarized in the x direction and
is the amplitude of the wave polarized in the x direction and  is the amplitude of the wave polarized in the y direction.
is the amplitude of the wave polarized in the y direction.The angles
 and
and  characterize the phase relationship between the wave polarized in x and the wave polarized in y.
characterize the phase relationship between the wave polarized in x and the wave polarized in y.The Jones vector contains all the polarization information for a plane wave. If the Jones vector for a sinusoidal plane wave, the amplitude
 , and the dispersion relationship
, and the dispersion relationship
are known, then the state of the wave is completely characterized.
Here
 is the angular frequency
is the angular frequencyAngular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
of the wave, and
 is the speed of light
is the speed of lightSpeed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
.
The notation for the Jones vector is the bra-ket notation
Bra-ket notation
Bra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...
of Dirac
Paul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
, which is normally used in a quantum context. The quantum notation is used here in anticipation of the interpretation of the Jones vector as a quantum state vector.
Dual of the Jones vector
The Jones vector has a dualDual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
given by

Normalization of the Jones vector
The Jones vector is normalized. The inner product of the vector with itself is unity.
Linear polarization

 are equal,
are equal,
This represents a wave with phase
Phase (waves)
Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
 polarized at an angle
polarized at an angle  with respect to the x axis. In that case the Jones vector can be written
with respect to the x axis. In that case the Jones vector can be written
The state vectors for linear polarization in x or y are special cases of this state vector.
If unit vectors are defined such that

and

then the linearly polarized polarization state can written in the "x-y basis" as

Circular polarization
If the phase angles and
and  differs by exactly
differs by exactly  and the x amplitude equals the y amplitude the wave is circularly polarized
and the x amplitude equals the y amplitude the wave is circularly polarizedCircular polarization
In electrodynamics, circular polarization of an electromagnetic wave is a polarization in which the electric field of the passing wave does not change strength but only changes direction in a rotary type manner....
. The Jones vector then becomes

where the plus sign indicates right circular polarization and the minus sign indicates left circular polarization. In the case of circular polarization, the electric field vector of constant magnitude rotates in the x-y plane.
If unit vectors are defined such that

and

then an arbitrary polarization state can written in the "R-L basis" as

where

and

We can see that

Elliptical polarization
The general case in which the electric field rotates in the x-y plane and has variable magnitude is called elliptical polarizationElliptical polarization
In electrodynamics, elliptical polarization is the polarization of electromagnetic radiation such that the tip of the electric field vector describes an ellipse in any fixed plane intersecting, and normal to, the direction of propagation...
. The state vector is given by

Geometric visualization of an arbitrary polarization state
To get an understanding of what a polarization state looks like, one can observe the orbit that is made if the polarization state is multiplied by a phase factor of and then having the real parts of its components interpreted as x and y coordinates respectively. That is:
and then having the real parts of its components interpreted as x and y coordinates respectively. That is:
If only the traced out shape and the direction of the rotation of is considered when interpreting the polarization state, i.e. only

(where and are defined as above) and whether it is overall more right circularly or left circularly polarized (i.e. whether or vice versa), it can be seen that the physical interpretation will be the same even if the state is multiplied by an arbitrary phase factor, since

and the direction of rotation will remain the same. In other words, there is no physical difference between two polarization states
 and
and  , between which only a phase factor differs.
, between which only a phase factor differs.It can be seen that for a linearly polarized state, M will be a line in the xy plane, with length 2 and its middle in the origin, and whose slope equals to . For a circularly polarized state, M will be a circle with radius and with the middle in the origin.
Energy in a plane wave
The energy per unit volumeEnergy density
Energy density is a term used for the amount of energy stored in a given system or region of space per unit volume. Often only the useful or extractable energy is quantified, which is to say that chemically inaccessible energy such as rest mass energy is ignored...
in classical electromagnetic fields is (cgs units)

For a plane wave, this becomes

where the energy has been averaged over a wavelength of the wave.
Fraction of energy in each component
The fraction of energy in the x component of the plane wave is
with a similar expression for the y component resulting in
 .
.The fraction in both components is

Momentum density of classical electromagnetic waves
The momentum density is given by the Poynting vectorPoynting vector
In physics, the Poynting vector can be thought of as representing the directional energy flux density of an electromagnetic field. It is named after its inventor John Henry Poynting. Oliver Heaviside and Nikolay Umov independently co-invented the Poynting vector...

For a sinusoidal plane wave traveling in the z direction, the momentum is in the z direction and is related to the energy density:

The momentum density has been averaged over a wavelength.
Angular momentum density of classical electromagnetic waves
Electromagnetic waves can have both orbital and spin angular momentum. The total angular momentum density is
For a sinusoidal plane wave propagating along
 axis the orbital angular momentum density vanishes. The spin angular momentum density is in the
axis the orbital angular momentum density vanishes. The spin angular momentum density is in the  direction and is given by
direction and is given by
where again the density is averaged over a wavelength.
Passage of a classical wave through a polaroid filter

Linear filter
Linear filters in the time domain process time-varying input signals to produce output signals, subject to the constraint of linearity.This results from systems composed solely of components classified as having a linear response....
transmits one component of a plane wave and absorbs the perpendicular component. In that case, if the filter is polarized in the x direction, the fraction of energy passing through the filter is

Example of energy conservation: Passage of a classical wave through a birefringent crystal
An ideal birefringentBirefringence
Birefringence, or double refraction, is the decomposition of a ray of light into two rays when it passes through certain anisotropic materials, such as crystals of calcite or boron nitride. The effect was first described by the Danish scientist Rasmus Bartholin in 1669, who saw it in calcite...
crystal transforms the polarization state of an electromagnetic wave without loss of wave energy. Birefringent crystals therefore provide an ideal test bed for examining the conservative transformation of polarization states. Even though this treatment is still purely classical, standard quantum tools such as unitary and Hermitian operators that evolve the state in time naturally emerge.
Initial and final states
A birefringent crystal is a material that has an optic axis with the property that the light has a different index of refraction for light polarized parallel to the axis than it has for light polarized perpendicular to the axis. Light polarized parallel to the axis are called "extraordinary rays" or "extraordinary photons", while light polarized perpendicular to the axis are called "ordinary rays" or "ordinary photons". If a linearly polarized wave impinges on the crystal, the extraordinary component of the wave will emerge from the crystal with a different phase than the ordinary component. In mathematical language, if the incident wave is linearly polarized at an angle with respect to the optic axis, the incident state vector can be written
with respect to the optic axis, the incident state vector can be written
and the state vector for the emerging wave can be written

While the initial state was linearly polarized, the final state is elliptically polarized. The birefringent crystal alters the character of the polarization.
Dual of the final state

Operator (physics)
In physics, an operator is a function acting on the space of physical states. As a resultof its application on a physical state, another physical state is obtained, very often along withsome extra relevant information....
U. The dual of the final state is given by

where
 is the adjoint
is the adjointHermitian adjoint
In mathematics, specifically in functional analysis, each linear operator on a Hilbert space has a corresponding adjoint operator.Adjoints of operators generalize conjugate transposes of square matrices to infinite-dimensional situations...
of U, the complex conjugate transpose of the matrix.
Unitary operators and energy conservation
The fraction of energy that emerges from the crystal is
In this ideal case, all the energy impinging on the crystal emerges from the crystal. An operator U with the property that

where I is the identity operator
Identity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
and U is called a unitary operator
Unitary operator
In functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
. The unitary property is necessary to ensure energy conservation
Energy conservation
Energy conservation refers to efforts made to reduce energy consumption. Energy conservation can be achieved through increased efficient energy use, in conjunction with decreased energy consumption and/or reduced consumption from conventional energy sources...
in state transformations.
Hermitian operators and energy conservation


and the adjoint by

Energy conservation then requires

This requires that

Operators like this that are equal to their adjoints are called Hermitian
Self-adjoint operator
In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
or self-adjoint.
The infinitesimal transition of the polarization state is

Thus, energy conservation requires that infinitesimal transformations of a polarization state occur through the action of a Hermitian operator.
Energy
The treatment to this point has been classicalClassical physics
What "classical physics" refers to depends on the context. When discussing special relativity, it refers to the Newtonian physics which preceded relativity, i.e. the branches of physics based on principles developed before the rise of relativity and quantum mechanics...
. It is a testament, however, to the generality of Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
for electrodynamics that the treatment can be made quantum mechanical
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
with only a reinterpretation of classical quantities. The reinterpretation is based on the theories of Max Planck
Max Planck
Max Karl Ernst Ludwig Planck, ForMemRS, was a German physicist who actualized the quantum physics, initiating a revolution in natural science and philosophy. He is regarded as the founder of the quantum theory, for which he received the Nobel Prize in Physics in 1918.-Life and career:Planck came...
and the interpretation by Albert Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
of those theories and of other experiments.
Einsteins's conclusion from early experiments on the photoelectric effect
Photoelectric effect
In the photoelectric effect, electrons are emitted from matter as a consequence of their absorption of energy from electromagnetic radiation of very short wavelength, such as visible or ultraviolet light. Electrons emitted in this manner may be referred to as photoelectrons...
is that electromagnetic radiation is composed of irreducible packets of energy, known as photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
s. The energy of each packet is related to the angular frequency of the wave by the relation

where
 is an experimentally determined quantity known as Planck's constant. If there are
is an experimentally determined quantity known as Planck's constant. If there are  photons in a box of volume
photons in a box of volume  , the energy in the electromagnetic field is
, the energy in the electromagnetic field is
and the energy density is

The energy of a photon can be related to classical fields through the correspondence principle
Correspondence principle
In physics, the correspondence principle states that the behavior of systems described by the theory of quantum mechanics reproduces classical physics in the limit of large quantum numbers....
which states that for a large number of photons, the quantum and classical treatments must agree. Thus, for very large
 , the quantum energy density must be the same as the classical energy density
, the quantum energy density must be the same as the classical energy density
The number of photons in the box is then

Momentum
The correspondence principle also determines the momentum and angular momentum of the photon. For momentum
which implies that the momentum of a photon is

Angular momentum and spin
Similarly for the spin angular momentum
which implies that the spin angular momentum of the photon is

the quantum interpretation of this expression is that the photon has a probability of
 of having a spin angular momentum of
of having a spin angular momentum of  and a probability of
and a probability of  of having a spin angular momentum of
of having a spin angular momentum of  . We can therefore think of the spin angular momentum of the photon being quantized as well as the energy. This has indeed been experimentally verified. Photons have only been observed to have spin angular momenta of
. We can therefore think of the spin angular momentum of the photon being quantized as well as the energy. This has indeed been experimentally verified. Photons have only been observed to have spin angular momenta of  .
.Spin operator
The spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
of the photon is defined as the coefficient of
 in the spin angular momentum calculation. A photon has spin 1 if it is in the
in the spin angular momentum calculation. A photon has spin 1 if it is in the  state and -1 if it is in the
state and -1 if it is in the  state. The spin operator is defined as the outer product
state. The spin operator is defined as the outer productOuter product
In linear algebra, the outer product typically refers to the tensor product of two vectors. The result of applying the outer product to a pair of vectors is a matrix...

The eigenvectors of the spin operator are
 and
and  with eigenvalues 1 and -1, respectively.
with eigenvalues 1 and -1, respectively.The expected value of a spin measurement on a photon is then

An operator S has been associated with an observable quantity, the spin angular momentum. The eigenvalues of the operator are the allowed observable values. This has been demonstrated for spin angular momentum, but it is in general true for any observable quantity.
Spin states
We can write the circularly polarized states as

where s=1 for

and s= -1 for

An arbitrary state can be written

where

Spin and angular momentum operators in differential form
When the state is written in spin notation, the spin operator can be written


The eigenvectors of the differential spin operator are

To see this note

The spin angular momentum operator is

Probability for a single photon
There are two ways in which probability can be applied to the behavior of photons; probability can be used to calculate the probable number of photons in a particular state, or probability can be used to calculate the likelihood of a single photon to be in a particular state. The former interpretation violates energy conservation. The latter interpretation is the viable, if nonintuitive, option. Dirac explains this in the context of the double-slit experimentDouble-slit experiment
The double-slit experiment, sometimes called Young's experiment, is a demonstration that matter and energy can display characteristics of both waves and particles...
:
Some time before the discovery of quantum mechanics people realized that the connection between light waves and photons must be of a statistical character. What they did not clearly realize, however, was that the wave function gives information about the probability of one photon being in a particular place and not the probable number of photons in that place. The importance of the distinction can be made clear in the following way. Suppose we have a beam of light consisting of a large number of photons split up into two components of equal intensity. On the assumption that the beam is connected with the probable number of photons in it, we should have half the total number going into each component. If the two components are now made to interfere, we should require a photon in one component to be able to interfere with one in the other. Sometimes these two photons would have to annihilate one another and other times they would have to produce four photons. This would contradict the conservation of energy. The new theory, which connects the wave function with probabilities for one photon gets over the difficulty by making each photon go partly into each of the two components. Each photon then interferes only with itself. Interference between two different photons never occurs.
—Paul Dirac, The Principles of Quantum Mechanics, Fourth Edition, Chapter 1
Probability amplitudes
The probability for a photon to be in a particular polarization state depends on the fields as calculated by the classical Maxwell's equations. The polarization state of the photon is proportional to the field. The probability itself is quadratic in the fields and consequently is also quadratic in the quantum state of polarization. In quantum mechanics, therefore, the state or probability amplitudeProbability amplitude
In quantum mechanics, a probability amplitude is a complex number whose modulus squared represents a probability or probability density.For example, if the probability amplitude of a quantum state is \alpha, the probability of measuring that state is |\alpha|^2...
contains the basic probability information. In general, the rules for combining probability amplitudes look very much like the classical rules for composition of probabilities: [The following quote is from Baym, Chapter 1]
- The probability amplitude for two successive probabilities is the product of amplitudes for the individual possibilities. For example, the amplitude for the x polarized photon to be right circularly polarized and for the right circularly polarized photon to pass through the y-polaroid is
 the product of the individual amplitudes.
the product of the individual amplitudes. - The amplitude for a process that can take place in one of several indistinguishable ways is the sum of amplitudes for each of the individual ways. For example, the total amplitude for the x polarized photon to pass through the y-polaroid is the sum of the amplitudes for it to pass as a right circularly polarized photon,
 plus the amplitude for it to pass as a left circularly polarized photon,
plus the amplitude for it to pass as a left circularly polarized photon, 
- The total probability for the process to occur is the absolute value squared of the total amplitude calculated by 1 and 2.
- The probability amplitude for two successive probabilities is the product of amplitudes for the individual possibilities. For example, the amplitude for the x polarized photon to be right circularly polarized and for the right circularly polarized photon to pass through the y-polaroid is
Uncertainty principle

Mathematical preparation
For any legal operators the following inequality, a consequence of the Cauchy-Schwarz inequality, is true.If B A ψ and A B ψ are defined then

where

is the operator mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
of observable X in the system state ψ and

Here

is called the commutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
of A and B.
This is a purely mathematical result. No reference has been made to any physical quantity or principle. It simply states that the uncertainty of an operator acting on a state times the uncertainty of another operator acting on the state is not necessarily zero.
Application to angular momentum
The connection to physics can be made if we identify the operators with physical operators such as the angular momentum and the polarization angle. We have then
which simply states that angular momentum and the polarization angle cannot be measured simultaneously with infinite accuracy.
States, probability amplitudes, unitary and Hermitian operators, and eigenvectors
Much of the mathematical apparatus of quantum mechanics appears in the classical description of a polarized sinusoidal electromagnetic wave. The Jones vector for a classical wave, for instance, is identical with the quantum polarization state vector for a photon. The right and left circular components of the Jones vector can be interpreted as probability amplitudeProbability amplitude
In quantum mechanics, a probability amplitude is a complex number whose modulus squared represents a probability or probability density.For example, if the probability amplitude of a quantum state is \alpha, the probability of measuring that state is |\alpha|^2...
s of spin states of the photon. Energy conservation requires that the states be transformed with a unitary operation. This implies that infinitesimal transformations are transformed with a Hermitian operator. These conclusions are a natural consequence of the structure of Maxwell's equations for classical waves.
Quantum mechanics enters the picture when observed quantities are measured and found to be discrete rather than continuous. The allowed observable values are determined by the eigenvalues of the operators associated with the observable. In the case angular momentum, for instance, the allowed observable values are the eigenvalues of the spin operator.
These concepts have emerged naturally from Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
and Planck's and Einstein's theories. They have been found to be true for many other physical systems. In fact, the typical program is to assume the concepts of this section and then to infer the unknown dynamics of a physical system. This was done, for instance, with the dynamics of electrons. In that case, working back from the principles in this section, the quantum dynamics of particles were inferred, leading to Schrödinger's equation, a departure from Newtonian mechanics. The solution of this equation for atoms led to the explanation of the Balmer series
Balmer series
The Balmer series or Balmer lines in atomic physics, is the designation of one of a set of six different named series describing the spectral line emissions of the hydrogen atom....
for atomic spectra and consequently formed a basis for all of atomic physics and chemistry.
This is not the only occasion in which Maxwell's equations have forced a restructuring of Newtonian mechanics. Maxwell's equations are relativistically consistent. Special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
resulted from attempts to make classical mechanics consistent with Maxwell's equations (see, for example, Moving magnet and conductor problem
Moving magnet and conductor problem
The moving magnet and conductor problem is a famous thought experiment, originating in the 19th century, concerning the intersection of classical electromagnetism and special relativity. In it, the current in a conductor moving with constant velocity, v, with respect to a magnet is calculated in...
).
See also
- Stern–Gerlach experimentStern–Gerlach experimentImportant in the field of quantum mechanics, the Stern–Gerlach experiment, named after Otto Stern and Walther Gerlach, is a 1922 experiment on the deflection of particles, often used to illustrate basic principles of quantum mechanics...
- Wave–particle dualityWave–particle dualityWave–particle duality postulates that all particles exhibit both wave and particle properties. A central concept of quantum mechanics, this duality addresses the inability of classical concepts like "particle" and "wave" to fully describe the behavior of quantum-scale objects...
- Double-slit experimentDouble-slit experimentThe double-slit experiment, sometimes called Young's experiment, is a demonstration that matter and energy can display characteristics of both waves and particles...
- Photon dynamics in the double-slit experimentPhoton dynamics in the double-slit experimentThe dynamics of photons in the double-slit experiment describes the relationship between classical electromagnetic waves and photons, the quantum counterpart of classical electromagnetic waves, in the context of the double-slit experiment....
- Theoretical and experimental justification for the Schrödinger equationTheoretical and experimental justification for the Schrödinger equationThe theoretical and experimental justification for the Schrödinger equation motivates the discovery of the Schrödinger equation, the equation that describes the dynamics of nonrelativistic particles...


