
Quadratic residue
Encyclopedia
In number theory
, an integer
q is called a quadratic residue modulo
n if it is congruent
to a perfect square
modulo n; i.e., if there exists an integer x such that:

Otherwise, q is called a quadratic nonresidue modulo n.
Originally an abstract mathematical
concept from the branch of number theory known as modular arithmetic, quadratic residues are now used in applications ranging from acoustical engineering to cryptography
and the factoring of large numbers.
, Legendre
, and other number theorists of the 17th and 18th centuries proved some theorems and made some conjectures about quadratic residues, but the first systematic treatment is § IV of Gauss's
Disquisitiones Arithmeticae
(1801). Article 95 introduces the terminology "quadratic residue" and "quadratic nonresidue", and states that, if the context makes it clear, the adjective "quadratic" may be dropped.
For a given n a list of the quadratic residues modulo n may be obtained by simply squaring the numbers 0, 1, …, n − 1. Because a2 ≡ (n − a)2 (mod n), the list of squares modulo n is symmetrical around n/2, and the list only needs to go that high. This can be seen in the table at the end of the article.
Thus, the number of quadratic residues modulo n cannot exceed n/2 + 1 (n even) or (n + 1)/2 (n odd).
The product of two residues is always a residue.
Modulo an odd prime number
p there are (p + 1)/2 residues (including 0) and (p − 1)/2 nonresidues. In this case, it is customary to consider 0 as a special case and work within the multiplicative group of nonzero elements
of the field
Z/pZ. (In other words, every congruence class except zero modulo p has a multiplicative inverse. This is not true for composite moduli.)
Following this convention, the multiplicative inverse of a residue is a residue, and the inverse of a nonresidue is a nonresidue.
Following this convention, modulo a prime number there are an equal number of residues and nonresidues.
Modulo a prime, the product of two nonresidues is a residue and the product of a nonresidue and a (nonzero) residue is a nonresidue.
The first supplement to the law of quadratic reciprocity is that if p ≡ 1 (mod 4) then −1 is a quadratic residue modulo p, and if p ≡ 3 (mod 4) then −1 is a nonresidue modulo p. This implies
If p ≡ 1 (mod 4) the negative of a residue modulo p is a residue and the negative of a nonresidue is a nonresidue.
If p ≡ 3 (mod 4) the negative of a residue modulo p is a nonresidue and the negative of a nonresidue is a residue.
So a nonzero number is a residue mod 8, 16, etc., if and only if it is of the form 4k(8n + 1).
A number A relatively prime to an odd prime p is a residue modulo any power of p if and only if it is a residue modulo p.
If the modulus is pn,
Notice that the rules are different for powers of two and powers of odd primes.
Modulo an odd prime power n = pk, the products of residues and nonresidues relatively prime to p obey the same rules as they do mod p; p is a nonresidue, and in general all the residues and nonresidues obey the same rules, except that the products will be zero if the power of p in the product ≥ n.
Modulo 8, the product of the nonresidues 3 and 5 is the nonresidue 7, and likewise for permutations of 3, 5 and 7. In fact, the multiplicative group of the non-residues and 1 form the Klein four-group
.
Modulo a composite number, the product of two residues is a residue. The product of a residue and a nonresidue may be a residue, a nonresidue, or zero.
Also, the product of two nonresidues may be either a residue, a nonresidue, or zero.
This phenomenon can best be described using the vocabulary of abstract algebra. The congruence classes relatively prime to the modulus are a group
under multiplication, called the group of units of the ring
Z/nZ, and the squares are a subgroup
of it. Different nonresidues may belong to different coset
s, and there is no simple rule that predicts which one their product will be in. Modulo a prime, there is only the subgroup of squares and a single coset.
The fact that, e.g., modulo 15 the product of the nonresidues 3 and 5, or of the nonresidue 5 and the residue 9, or the two residues 9 and 10 are all zero comes from working in the full ring Z/nZ, which has zero divisor
s for composite n.
For this reason some authors add to the definition that a quadratic residue q must not only be a square but must also be relatively prime to the modulus n.
Although it makes things tidier, this article does not insist that residues must be coprime to the modulus.
Although this notation is compact and convenient for some purposes, the most useful notation is the Legendre symbol
, also called the quadratic character, which is defined for all integers a and positive odd prime numbers p as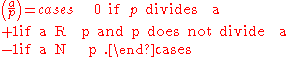
There are two reasons why numbers ≡ 0 (mod p) are treated specially. As we have seen, it makes many formulas and theorems easier to state. The other (related) reason is that the quadratic character is a homomorphism
from the multiplicative group of nonzero conguence classes modulo p
to the complex numbers. Setting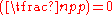 allows its domain
allows its domain
to be extended to the multiplicative semigroup
of all the integers.
One advantage of this notation over Gauss's is that the Legendre symbol is a function that can be used in formulas. It can also easily be generalized to cubic
, quartic and higher power residues.
There is a generalization of the Legendre symbol for composite values of p, the Jacobi symbol
, but its properties are not as simple: if m is composite and the Jacobi symbol then a N m, and if a R m then
then a N m, and if a R m then  but if
but if 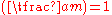 we do not know whether a R m or a N m. If m is prime, the Jacobi and Legendre symbols agree.
we do not know whether a R m or a N m. If m is prime, the Jacobi and Legendre symbols agree.
Using Dirichlet's theorem
on primes in arithmetic progressions, the law of quadratic reciprocity, and the Chinese remainder theorem
(CRT) it is easy to see that for any M > 0 there are primes p such that the numbers 1, 2, …, M are all residues modulo p.
for the class number of binary quadratic form
s. Let q be a prime number, s a complex variable, and define a Dirichlet L-function as
Dirichlet showed that if q ≡ 3 (mod 4), then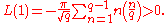
Therefore, in this case (prime q ≡ 3 (mod 4)), the sum of the quadratic residues minus the sum of the nonresidues in the range 1, 2, …, q − 1 is a negative number.
In fact the difference will always be an odd multiple of q if q > 3. In contrast, for prime q ≡ 1 (mod 4), the sum of the quadratic residues minus the sum of the nonresidues in the range 1, 2, …, q − 1 is zero, implying that both sums equal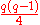 .
.
Dirichlet also proved that for prime q ≡ 3 (mod 4),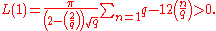
This implies that there are more quadratic residues than nonresidues among the numbers 1, 2, …, (q − 1)/2.
An intriguing fact about these two theorems is that all known proofs rely on analysis; no-one has ever published a simple or direct proof of either statement.
Let p be an odd prime. For i, j = 0, 1 define the sets
and let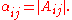
That is,
Then if p ≡ 1 (mod 4)
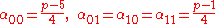
and if p ≡ 3 (mod 4)
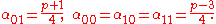
Gauss (1828) introduced this sort of counting when he proved that if p ≡ 1 (mod 4) then x4 ≡ 2 (mod p) can be solved if and only if p = a2 + 64 b2.
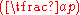 for consecutive values of a mimic a random variable like a coin flip. Specifically,
for consecutive values of a mimic a random variable like a coin flip. Specifically,
Pólya
and Vinogradov proved (independently) in 1918 that for any nonprincipal Dirichlet character
χ(n) modulo q and any integers M and N,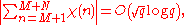 in big O notation
in big O notation
. Setting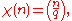
this shows that the number of quadratic residues modulo q in any interval of length N is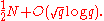 It is easy to prove that
It is easy to prove that 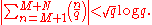
In fact,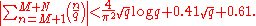
Montgomery and Vaughan improved this in 1977, showing that, if the generalized Riemann hypothesis
is true then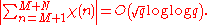
This result cannot be substantially improved, for Schur
had proved in 1918 that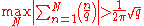
and Paley
had proved in 1932 that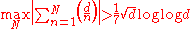
for infinitely many d > 0.
An important difference between prime and composite moduli shows up here. Modulo a prime p, a quadratic residue a has 1 + (a|p) roots (i.e. zero if a N p, one if a ≡ 0 (mod p), or two if a R p and gcd(a,p) = 1.)
In general if a composite modulus n is written as a product of powers of distinct primes, and there are n1 roots modulo the first one, n2 mod the second, …, there will be n1n2… roots modulo n.
The theoretical way solutions modulo the prime powers are combined to make solutions modulo n is called the Chinese remainder theorem
; it can be implemented with an efficient algorithm.
(a|n) can be quickly computed using a variation of Euclid's algorithm.; if it is −1 there is no solution.
Secondly, assuming that (a|n) = 1, if n ≡ 3 (mod 4), Lagrange
found that the solutions are given by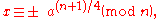
and Legendre
found a similar solution if n ≡ 5 (mod 8).
For prime n ≡ 1 (mod 8), however, there is no known formula. Tonelli (in 1891) and Cipolla found efficient algorithms that work for all prime moduli. Both algorithms require finding a quadratic nonresidue modulo n, and there is no efficient deterministic algorithm known for doing that. But since half the numbers between 1 and n are nonresidues, picking numbers x at random and calculating the Legendre symbol (x|n) until a nonresidue is found will quickly produce one.
If the modulus n is a prime power n = pe, a solution may be found modulo p and "lifted" to a solution modulo n using Hensel's lemma
or an algorithm of Gauss.
If the Jacobi symbol (a|n) = −1 then there is no solution. If it is +1, there may or may not be one.
If the factorization of n is not known, and (a|n) = 1, the problem is known to be equivalent to integer factorization
of n (i.e. an efficient solution to either problem could be used to solve the other efficiently).
Simply determining whether a N n or a R n (which can be done efficiently for prime n by computing the Legendre symbol) is known as the quadratic residuosity problem
when n is composite. It is not known to be as hard as factorization, but is thought to be quite hard.
On the other hand, if we want to know if there is a solution for x less than some given limit c, this problem is NP-complete
; however, this is a fixed-parameter tractable problem, where c is the parameter.
In general, to determine if a quadratic congruence with composite modulus is solvable use the following theorem :
Let n > 1, and gcd(a,n) =1. Then x2 ≡ a (mod n) is solvable if and only if:
a) The Legendre symbol, (a/p) = 1 for all odd prime divisors of n.
b) a = 1 (mod 4) if 4|n, but 8 does not divide n; a ≡ 1 (mod 8) if 8|n.
Note: This theorem essentially requires that the factorization of n is known. Also notice that if gcd(a,n)=m, then the congruence can be reduced to a/m ≡ x2/m (mod n/m), but then this takes the problem away from being a problem of quadratic congruences (unless m is a square).
and quadratic residues.
s are dense undirected graphs, one for each prime p ≡ 1 (mod 4), that form an infinite family of conference graph
s, which yield an infinite family of symmetric conference matrices
.
Paley digraphs are directed analogs of Paley graphs, one for each p ≡ 3 (mod 4), that yield antisymmetric
conference matrices.
The construction of these graphs uses quadratic residues.
such as the Rabin cryptosystem
and the oblivious transfer
. The quadratic residuosity problem
is the basis for the Goldwasser-Micali cryptosystem
.
The discrete logarithm
is a similar problem that is also used in cryptography.
is a formula for the Legendre symbol (a|p) where p is prime. If p is composite the formula may or may not compute (a|p) correctly. The Solovay-Strassen primality test
for whether a given number n is prime or composite picks a random a and computes (a|n) using a modification of Euclid's algorithm, and also using Euler's criterion. If the results disagree, n is composite; if they agree, n may be composite or prime. For a composite n at least 1/2 the values of a in the range 2, 3, ..., n − 1 will return "n is composite"; for prime n none will. If, after using many different values of a, n has not been proved composite it is called a "probable prime".
The Miller-Rabin primality test
is based on the same principles. There is a deterministic version of it, but the proof that it works depends on the generalized Riemann hypothesis
; the output from this test is "n is definitely composite" or "either n is prime or the GRH is false". If the second output ever occurs for a composite n, then the GRH would be false, which would have implications through many branches of mathematics.
Several modern factorization algorithms (including Dixon's algorithm, the continued fraction method
, the quadratic sieve
, and the number field sieve
) generate small quadratic residues (modulo the number being factorized) in an attempt to find a congruence of squares
which will yield a factorization. The number field sieve is the fastest general-purpose factorization algorithm known.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, an integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
q is called a quadratic residue modulo
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
n if it is congruent
Congruence relation
In abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...
to a perfect square
Square number
In mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself...
modulo n; i.e., if there exists an integer x such that:

Otherwise, q is called a quadratic nonresidue modulo n.
Originally an abstract mathematical
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
concept from the branch of number theory known as modular arithmetic, quadratic residues are now used in applications ranging from acoustical engineering to cryptography
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
and the factoring of large numbers.
History, conventions, and elementary facts
Fermat, Euler, LagrangeJoseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
, Legendre
Adrien-Marie Legendre
Adrien-Marie Legendre was a French mathematician.The Moon crater Legendre is named after him.- Life :...
, and other number theorists of the 17th and 18th centuries proved some theorems and made some conjectures about quadratic residues, but the first systematic treatment is § IV of Gauss's
Gauss
Gauss may refer to:*Carl Friedrich Gauss, German mathematician and physicist*Gauss , a unit of magnetic flux density or magnetic induction*GAUSS , a software package*Gauss , a crater on the moon...
Disquisitiones Arithmeticae
Disquisitiones Arithmeticae
The Disquisitiones Arithmeticae is a textbook of number theory written in Latin by Carl Friedrich Gauss in 1798 when Gauss was 21 and first published in 1801 when he was 24...
(1801). Article 95 introduces the terminology "quadratic residue" and "quadratic nonresidue", and states that, if the context makes it clear, the adjective "quadratic" may be dropped.
For a given n a list of the quadratic residues modulo n may be obtained by simply squaring the numbers 0, 1, …, n − 1. Because a2 ≡ (n − a)2 (mod n), the list of squares modulo n is symmetrical around n/2, and the list only needs to go that high. This can be seen in the table at the end of the article.
Thus, the number of quadratic residues modulo n cannot exceed n/2 + 1 (n even) or (n + 1)/2 (n odd).
The product of two residues is always a residue.
Prime modulus
Modulo 2, every integer is a quadratic residue.Modulo an odd prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p there are (p + 1)/2 residues (including 0) and (p − 1)/2 nonresidues. In this case, it is customary to consider 0 as a special case and work within the multiplicative group of nonzero elements
Multiplicative group of integers modulo n
In modular arithmetic the set of congruence classes relatively prime to the modulus n form a group under multiplication called the multiplicative group of integers modulo n. It is also called the group of primitive residue classes modulo n. In the theory of rings, a branch of abstract algebra, it...
of the field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
Z/pZ. (In other words, every congruence class except zero modulo p has a multiplicative inverse. This is not true for composite moduli.)
Following this convention, the multiplicative inverse of a residue is a residue, and the inverse of a nonresidue is a nonresidue.
Following this convention, modulo a prime number there are an equal number of residues and nonresidues.
Modulo a prime, the product of two nonresidues is a residue and the product of a nonresidue and a (nonzero) residue is a nonresidue.
The first supplement to the law of quadratic reciprocity is that if p ≡ 1 (mod 4) then −1 is a quadratic residue modulo p, and if p ≡ 3 (mod 4) then −1 is a nonresidue modulo p. This implies
If p ≡ 1 (mod 4) the negative of a residue modulo p is a residue and the negative of a nonresidue is a nonresidue.
If p ≡ 3 (mod 4) the negative of a residue modulo p is a nonresidue and the negative of a nonresidue is a residue.
Prime power modulus
All odd squares are ≡ 1 (mod 8) and a fortiori ≡ 1 (mod 4). If a is an odd number and m = 8, 16, or some higher power of 2, then a is a residue modulo m if and only if a ≡ 1 (mod 8).For example, mod (32) the odd squares are
- 12 ≡ 152 ≡ 1
- 32 ≡ 132 ≡ 9
- 52 ≡ 112 ≡ 25
- 72 ≡ 92 ≡ 17
and the even ones are
- 02 ≡ 82 ≡ 162 ≡ 0
- 22 ≡ 62≡ 102 ≡ 142≡ 4
- 42 ≡ 122 ≡ 16
So a nonzero number is a residue mod 8, 16, etc., if and only if it is of the form 4k(8n + 1).
A number A relatively prime to an odd prime p is a residue modulo any power of p if and only if it is a residue modulo p.
If the modulus is pn,
- then pkA
- is a residue modulo pn if k ≥ n
- is a nonresidue modulo pn if k < n is odd
- is a residue modulo pn if k < n is even and A is a residue
- is a nonresidue modulo pn if k < n is even and A is a nonresidue.
Notice that the rules are different for powers of two and powers of odd primes.
Modulo an odd prime power n = pk, the products of residues and nonresidues relatively prime to p obey the same rules as they do mod p; p is a nonresidue, and in general all the residues and nonresidues obey the same rules, except that the products will be zero if the power of p in the product ≥ n.
Modulo 8, the product of the nonresidues 3 and 5 is the nonresidue 7, and likewise for permutations of 3, 5 and 7. In fact, the multiplicative group of the non-residues and 1 form the Klein four-group
Klein four-group
In mathematics, the Klein four-group is the group Z2 × Z2, the direct product of two copies of the cyclic group of order 2...
.
Composite modulus not a prime power
The basic fact in this case is- if a is a residue modulo n, then a is a residue modulo pk for every prime power dividing n.
- if a is a nonresidue modulo n, then a is a nonresidue modulo pk for at least one prime power dividing n.
Modulo a composite number, the product of two residues is a residue. The product of a residue and a nonresidue may be a residue, a nonresidue, or zero.
For example, from the table for modulus 6
1, 2, 3, 4, 5 (residues in bold).
The product of the residue 3 and the nonresidue 5 is the residue 3, whereas the product of the residue 4 and the nonresidue 2 is the nonresidue 2.
Also, the product of two nonresidues may be either a residue, a nonresidue, or zero.
For example, from the table for modulus 15
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 (residues in bold).
The product of the nonresidues 2 and 8 is the residue 1, whereas the product of the nonresidues 2 and 7 is the nonresidue 14.
This phenomenon can best be described using the vocabulary of abstract algebra. The congruence classes relatively prime to the modulus are a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
under multiplication, called the group of units of the ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
Z/nZ, and the squares are a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of it. Different nonresidues may belong to different coset
Coset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
s, and there is no simple rule that predicts which one their product will be in. Modulo a prime, there is only the subgroup of squares and a single coset.
The fact that, e.g., modulo 15 the product of the nonresidues 3 and 5, or of the nonresidue 5 and the residue 9, or the two residues 9 and 10 are all zero comes from working in the full ring Z/nZ, which has zero divisor
Zero divisor
In abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
s for composite n.
For this reason some authors add to the definition that a quadratic residue q must not only be a square but must also be relatively prime to the modulus n.
Although it makes things tidier, this article does not insist that residues must be coprime to the modulus.
Notations
Gauss used R and N to denote residuacity and non-residuacity, respectively;- for example, 2 R 7 and 5 N 7, or 1 R 8 and 3,5,7 N 8.
Although this notation is compact and convenient for some purposes, the most useful notation is the Legendre symbol
Legendre symbol
In number theory, the Legendre symbol is a multiplicative function with values 1, −1, 0 that is a quadratic character modulo a prime number p: its value on a quadratic residue mod p is 1 and on a quadratic non-residue is −1....
, also called the quadratic character, which is defined for all integers a and positive odd prime numbers p as
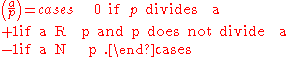
There are two reasons why numbers ≡ 0 (mod p) are treated specially. As we have seen, it makes many formulas and theorems easier to state. The other (related) reason is that the quadratic character is a homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
from the multiplicative group of nonzero conguence classes modulo p
Multiplicative group of integers modulo n
In modular arithmetic the set of congruence classes relatively prime to the modulus n form a group under multiplication called the multiplicative group of integers modulo n. It is also called the group of primitive residue classes modulo n. In the theory of rings, a branch of abstract algebra, it...
to the complex numbers. Setting
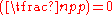 allows its domain
allows its domainDomain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
to be extended to the multiplicative semigroup
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
of all the integers.
One advantage of this notation over Gauss's is that the Legendre symbol is a function that can be used in formulas. It can also easily be generalized to cubic
Cubic reciprocity
Cubic reciprocity is a collection of theorems in elementary and algebraic number theory that state conditions under which the congruence x3 ≡ p is solvable; the word "reciprocity" comes from the form of the main theorem, which states that if p and q are primary numbers in the...
, quartic and higher power residues.
There is a generalization of the Legendre symbol for composite values of p, the Jacobi symbol
Jacobi symbol
The Jacobi symbol is a generalization of the Legendre symbol. Introduced by Jacobi in 1837, it is of theoretical interest in modular arithmetic and other branches of number theory, but its main use is in computational number theory, especially primality testing and integer factorization; these in...
, but its properties are not as simple: if m is composite and the Jacobi symbol
 then a N m, and if a R m then
then a N m, and if a R m then  but if
but if 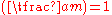 we do not know whether a R m or a N m. If m is prime, the Jacobi and Legendre symbols agree.
we do not know whether a R m or a N m. If m is prime, the Jacobi and Legendre symbols agree.Distribution of quadratic residues
Although quadratic residues appear to occur in a rather random pattern modulo n, and this has been exploited in such applications as acoustics and cryptography, their distribution also exhibits some striking regularities.Using Dirichlet's theorem
Dirichlet's theorem on arithmetic progressions
In number theory, Dirichlet's theorem, also called the Dirichlet prime number theorem, states that for any two positive coprime integers a and d, there are infinitely many primes of the form a + nd, where n ≥ 0. In other words, there are infinitely many primes which are...
on primes in arithmetic progressions, the law of quadratic reciprocity, and the Chinese remainder theorem
Chinese remainder theorem
The Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
(CRT) it is easy to see that for any M > 0 there are primes p such that the numbers 1, 2, …, M are all residues modulo p.
For example, if p ≡ 1 (mod 8), (mod 12), (mod 5) and (mod 28), then by the law of quadratic reciprocity 2, 3, 5, and 7 will all be residues modulo p, and thus all numbers 1–10 will be. The CRT says that this is the same as p ≡ 1 (mod 840), and Dirichlet's theorem says there are an infinite number of primes of this form. 2521 is the smallest, and indeed 12 ≡ 1, 10462 ≡ 2, 1232 ≡ 3, 22 ≡ 4, 6432 ≡ 5, 872 ≡ 6, 6682 ≡ 7, 4292 ≡ 8, 32 ≡ 9, and 5292 ≡ 10 (mod 2521).
Dirichlet's formulas
The first of these regularities stems from Dirichlet's work (in the 1830s) on the analytic formulaClass number formula
In number theory, the class number formula relates many important invariants of a number field to a special value of its Dedekind zeta function-General statement of the class number formula:...
for the class number of binary quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
s. Let q be a prime number, s a complex variable, and define a Dirichlet L-function as

Dirichlet showed that if q ≡ 3 (mod 4), then
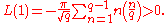
Therefore, in this case (prime q ≡ 3 (mod 4)), the sum of the quadratic residues minus the sum of the nonresidues in the range 1, 2, …, q − 1 is a negative number.
For example, modulo 11,
- 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 (residues in bold)
- 1 + 4 + 9 + 5 + 3 = 22, 2 + 6 + 7 + 8 + 10 = 33, and the difference is −11.
In fact the difference will always be an odd multiple of q if q > 3. In contrast, for prime q ≡ 1 (mod 4), the sum of the quadratic residues minus the sum of the nonresidues in the range 1, 2, …, q − 1 is zero, implying that both sums equal
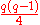 .
.Dirichlet also proved that for prime q ≡ 3 (mod 4),
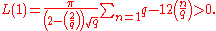
This implies that there are more quadratic residues than nonresidues among the numbers 1, 2, …, (q − 1)/2.
For example, modulo 11 there are four residues less than 6 (namely 1, 3, 4, and 5), but only one nonresidue (2).
An intriguing fact about these two theorems is that all known proofs rely on analysis; no-one has ever published a simple or direct proof of either statement.
Pairs of residues and nonresidues
Modulo a prime p, the number of pairs n, n + 1 where n R p and n + 1 R p, or n N p and n + 1 R p, etc., are almost equal. More precisely,Let p be an odd prime. For i, j = 0, 1 define the sets

and let
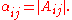
That is,
- α00 is the number of residues that are followed by a residue,
- α01 is the number of residues that are followed by a nonresidue,
- α10 is the number of nonresidues that are followed by a residue, and
- α11 is the number of nonresidues that are followed by a nonresidue.
Then if p ≡ 1 (mod 4)
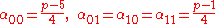
and if p ≡ 3 (mod 4)
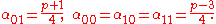
For example: (residues in bold)
Modulo 17
- 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16
- A00 = {1,8,15},
- A01 = {2,4,9,13},
- A10 = {3,7,12,14},
- A11 = {5,6,10,11}.
Modulo 19
- 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18
- A00 = {4,5,6,16},
- A01 = {1,7,9,11,17},
- A10 = {3,8,10,15},
- A11 = {2,12,13,14}.
Gauss (1828) introduced this sort of counting when he proved that if p ≡ 1 (mod 4) then x4 ≡ 2 (mod p) can be solved if and only if p = a2 + 64 b2.
The Pólya–Vinogradov inequality
The values of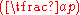 for consecutive values of a mimic a random variable like a coin flip. Specifically,
for consecutive values of a mimic a random variable like a coin flip. Specifically,Pólya
George Pólya
George Pólya was a Hungarian mathematician. He was a professor of mathematics from 1914 to 1940 at ETH Zürich and from 1940 to 1953 at Stanford University. He made fundamental contributions to combinatorics, number theory, numerical analysis and probability theory...
and Vinogradov proved (independently) in 1918 that for any nonprincipal Dirichlet character
Dirichlet character
In number theory, Dirichlet characters are certain arithmetic functions which arise from completely multiplicative characters on the units of \mathbb Z / k \mathbb Z...
χ(n) modulo q and any integers M and N,
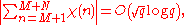 in big O notation
in big O notationBig O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
. Setting
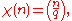
this shows that the number of quadratic residues modulo q in any interval of length N is
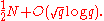 It is easy to prove that
It is easy to prove that 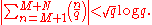
In fact,
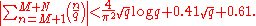
Montgomery and Vaughan improved this in 1977, showing that, if the generalized Riemann hypothesis
Generalized Riemann hypothesis
The Riemann hypothesis is one of the most important conjectures in mathematics. It is a statement about the zeros of the Riemann zeta function. Various geometrical and arithmetical objects can be described by so-called global L-functions, which are formally similar to the Riemann zeta-function...
is true then
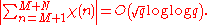
This result cannot be substantially improved, for Schur
Issai Schur
Issai Schur was a mathematician who worked in Germany for most of his life. He studied at Berlin...
had proved in 1918 that
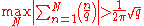
and Paley
Raymond Paley
Raymond Edward Alan Christopher Paley was an English mathematician. Paley was born in Bournemouth, England. He was educated at Eton. From there he entered Trinity College, Cambridge where he showed himself the most brilliant student among a remarkable collection of fellow undergraduates...
had proved in 1932 that
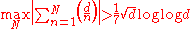
for infinitely many d > 0.
Complexity of finding square roots
That is, given a number a and a modulus n, how hard is it- to tell whether an x solving x2 ≡ a (mod n) exists
- assuming one does exist, to calculate it?
An important difference between prime and composite moduli shows up here. Modulo a prime p, a quadratic residue a has 1 + (a|p) roots (i.e. zero if a N p, one if a ≡ 0 (mod p), or two if a R p and gcd(a,p) = 1.)
In general if a composite modulus n is written as a product of powers of distinct primes, and there are n1 roots modulo the first one, n2 mod the second, …, there will be n1n2… roots modulo n.
The theoretical way solutions modulo the prime powers are combined to make solutions modulo n is called the Chinese remainder theorem
Chinese remainder theorem
The Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
; it can be implemented with an efficient algorithm.
For example:
- Solve x2 ≡ 6 (mod 15).
- x2 ≡ 6 (mod 3) has one solution, 0; x2 ≡ 6 (mod 5) has two, 1 and 4.
- and there are two solutions modulo 15, namely 6 and 9.
- Solve x2 ≡ 4 (mod 15).
- x2 ≡ 4 (mod 3) has two solutions, 1 and 2; x2 ≡ 4 (mod 5) has two, 2 and 3.
- and there are four solutions modulo 15, namely 2, 7, 8, and 13.
Prime or prime power modulus
First off, if the modulus n is prime the Legendre symbolLegendre symbol
In number theory, the Legendre symbol is a multiplicative function with values 1, −1, 0 that is a quadratic character modulo a prime number p: its value on a quadratic residue mod p is 1 and on a quadratic non-residue is −1....
(a|n) can be quickly computed using a variation of Euclid's algorithm.; if it is −1 there is no solution.
Secondly, assuming that (a|n) = 1, if n ≡ 3 (mod 4), Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
found that the solutions are given by
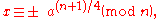
and Legendre
Adrien-Marie Legendre
Adrien-Marie Legendre was a French mathematician.The Moon crater Legendre is named after him.- Life :...
found a similar solution if n ≡ 5 (mod 8).
For prime n ≡ 1 (mod 8), however, there is no known formula. Tonelli (in 1891) and Cipolla found efficient algorithms that work for all prime moduli. Both algorithms require finding a quadratic nonresidue modulo n, and there is no efficient deterministic algorithm known for doing that. But since half the numbers between 1 and n are nonresidues, picking numbers x at random and calculating the Legendre symbol (x|n) until a nonresidue is found will quickly produce one.
If the modulus n is a prime power n = pe, a solution may be found modulo p and "lifted" to a solution modulo n using Hensel's lemma
Hensel's lemma
In mathematics, Hensel's lemma, also known as Hensel's lifting lemma, named after Kurt Hensel, is a result in modular arithmetic, stating that if a polynomial equation has a simple root modulo a prime number , then this root corresponds to a unique root of the same equation modulo any higher power...
or an algorithm of Gauss.
Composite modulus
If the modulus n has been factored into prime powers the solution was discussed above.If the Jacobi symbol (a|n) = −1 then there is no solution. If it is +1, there may or may not be one.
If the factorization of n is not known, and (a|n) = 1, the problem is known to be equivalent to integer factorization
Integer factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
of n (i.e. an efficient solution to either problem could be used to solve the other efficiently).
The above discussion indicates how knowing the factors of n allows us to find the roots efficiently. Say there were an efficient algorithm for finding square roots modulo a composite number. The article congruence of squaresCongruence of squaresIn number theory, a congruence of squares is a congruence commonly used in integer factorization algorithms.-Derivation:Given a positive integer n, Fermat's factorization method relies on finding numbers x, y satisfying the equality...
discusses how finding two numbers x and y where x2 ≡ y2 (mod n) and x ≠ ±y suffices to factorize n efficiently. Generate a random number, square it modulo n, and have the efficient square root algorithm find a root. Repeat until it returns a number not equal to the one we originally squared (or its negative modulo n), then follow the algorithm described in congruence of squares. The efficiency of the factoring algorithm depends on the exact characteristics of the root-finder (e.g. does it return all roots? just the smallest one? a random one?), but it will be efficient.
Simply determining whether a N n or a R n (which can be done efficiently for prime n by computing the Legendre symbol) is known as the quadratic residuosity problem
Quadratic residuosity problem
The quadratic residuosity problem in computational number theory is the question of distinguishing by calculating the quadratic residues modulo N, where N is a composite number...
when n is composite. It is not known to be as hard as factorization, but is thought to be quite hard.
On the other hand, if we want to know if there is a solution for x less than some given limit c, this problem is NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
; however, this is a fixed-parameter tractable problem, where c is the parameter.
In general, to determine if a quadratic congruence with composite modulus is solvable use the following theorem :
Let n > 1, and gcd(a,n) =1. Then x2 ≡ a (mod n) is solvable if and only if:
a) The Legendre symbol, (a/p) = 1 for all odd prime divisors of n.
b) a = 1 (mod 4) if 4|n, but 8 does not divide n; a ≡ 1 (mod 8) if 8|n.
Note: This theorem essentially requires that the factorization of n is known. Also notice that if gcd(a,n)=m, then the congruence can be reduced to a/m ≡ x2/m (mod n/m), but then this takes the problem away from being a problem of quadratic congruences (unless m is a square).
Acoustics
Sound diffusers have been based on number-theoretic concepts such as primitive rootsPrimitive root modulo n
In modular arithmetic, a branch of number theory, a primitive root modulo n is any number g with the property that any number coprime to n is congruent to a power of g modulo n. In other words, g is a generator of the multiplicative group of integers modulo n...
and quadratic residues.
Graph theory
Paley graphPaley graph
In mathematics, and specifically graph theory, Paley graphs, named after Raymond Paley, are dense undirected graphs constructed from the members of a suitable finite field by connecting pairs of elements that differ in a quadratic residue. The Paley graphs form an infinite family of conference...
s are dense undirected graphs, one for each prime p ≡ 1 (mod 4), that form an infinite family of conference graph
Conference graph
In the mathematical area of graph theory, a conference graph is a strongly regular graph with parameters v, and It is the graph associated with a symmetric conference matrix, and consequently its order v must be 1 and a sum of two squares....
s, which yield an infinite family of symmetric conference matrices
Conference matrix
In mathematics, a conference matrix is a square matrix C with 0 on the diagonal and +1 and −1 off the diagonal, such that CTC is a multiple of the identity matrix I...
.
Paley digraphs are directed analogs of Paley graphs, one for each p ≡ 3 (mod 4), that yield antisymmetric
Skew-symmetric matrix
In mathematics, and in particular linear algebra, a skew-symmetric matrix is a square matrix A whose transpose is also its negative; that is, it satisfies the equation If the entry in the and is aij, i.e...
conference matrices.
The construction of these graphs uses quadratic residues.
Cryptography
The fact that finding a square root of a number modulo a large composite n is equivalent to factoring (which is widely believed be a hard problem) has been used for constructing cryptographic schemesCryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
such as the Rabin cryptosystem
Rabin cryptosystem
The Rabin cryptosystem is an asymmetric cryptographic technique, whose security, like that of RSA, is related to the difficulty of factorization. However the Rabin cryptosystem has the advantage that the problem on which it relies has been proved to be as hard as integer factorization, which is...
and the oblivious transfer
Oblivious transfer
In cryptography, an oblivious transfer protocol is a type of protocol in which a sender transfers one of potentially many pieces of information to a receiver, but remains oblivious as to what piece has been transferred....
. The quadratic residuosity problem
Quadratic residuosity problem
The quadratic residuosity problem in computational number theory is the question of distinguishing by calculating the quadratic residues modulo N, where N is a composite number...
is the basis for the Goldwasser-Micali cryptosystem
Goldwasser-Micali cryptosystem
The Goldwasser–Micali cryptosystem is an asymmetric key encryption algorithm developed by Shafi Goldwasser and Silvio Micali in 1982. GM has the distinction of being the first probabilistic public-key encryption scheme which is provably secure under standard cryptographic assumptions...
.
The discrete logarithm
Discrete logarithm
In mathematics, specifically in abstract algebra and its applications, discrete logarithms are group-theoretic analogues of ordinary logarithms. In particular, an ordinary logarithm loga is a solution of the equation ax = b over the real or complex numbers...
is a similar problem that is also used in cryptography.
Primality testing
Euler's criterionEuler's criterion
In mathematics, Euler's criterion is used in determining in number theory whether a given integer is a quadratic residue modulo a prime.-Definition:Euler's criterion states:Let p be an odd prime and a an integer coprime to p. Then...
is a formula for the Legendre symbol (a|p) where p is prime. If p is composite the formula may or may not compute (a|p) correctly. The Solovay-Strassen primality test
Solovay-Strassen primality test
The Solovay–Strassen primality test, developed by Robert M. Solovay and Volker Strassen, is a probabilistic test to determine if a number is composite or probably prime...
for whether a given number n is prime or composite picks a random a and computes (a|n) using a modification of Euclid's algorithm, and also using Euler's criterion. If the results disagree, n is composite; if they agree, n may be composite or prime. For a composite n at least 1/2 the values of a in the range 2, 3, ..., n − 1 will return "n is composite"; for prime n none will. If, after using many different values of a, n has not been proved composite it is called a "probable prime".
The Miller-Rabin primality test
Miller-Rabin primality test
The Miller–Rabin primality test or Rabin–Miller primality test is a primality test: an algorithmwhich determines whether a given number is prime,...
is based on the same principles. There is a deterministic version of it, but the proof that it works depends on the generalized Riemann hypothesis
Generalized Riemann hypothesis
The Riemann hypothesis is one of the most important conjectures in mathematics. It is a statement about the zeros of the Riemann zeta function. Various geometrical and arithmetical objects can be described by so-called global L-functions, which are formally similar to the Riemann zeta-function...
; the output from this test is "n is definitely composite" or "either n is prime or the GRH is false". If the second output ever occurs for a composite n, then the GRH would be false, which would have implications through many branches of mathematics.
Integer factorization
In § VI of the Disquisitiones Arithmeticae Gauss discusses two factoring algorithms that use quadratic residues and the law of quadratic reciprocity.Several modern factorization algorithms (including Dixon's algorithm, the continued fraction method
Continued fraction factorization
In number theory, the continued fraction factorization method is an integer factorization algorithm. It is a general-purpose algorithm, meaning that it is suitable for factoring any integer n, not depending on special form or properties. It was described by D. H. Lehmer and R. E. Powers in 1931,...
, the quadratic sieve
Quadratic sieve
The quadratic sieve algorithm is a modern integer factorization algorithm and, in practice, the second fastest method known . It is still the fastest for integers under 100 decimal digits or so, and is considerably simpler than the number field sieve...
, and the number field sieve
General number field sieve
In number theory, the general number field sieve is the most efficient classical algorithm known for factoring integers larger than 100 digits...
) generate small quadratic residues (modulo the number being factorized) in an attempt to find a congruence of squares
Congruence of squares
In number theory, a congruence of squares is a congruence commonly used in integer factorization algorithms.-Derivation:Given a positive integer n, Fermat's factorization method relies on finding numbers x, y satisfying the equality...
which will yield a factorization. The number field sieve is the fastest general-purpose factorization algorithm known.
Table of quadratic residues
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x2 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | 121 | 144 | 169 | 196 | 225 | 256 | 289 | 324 | 361 | 400 | 441 | 484 | 529 | 576 | 625 |
| mod 2 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| mod 3 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| mod 4 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| mod 5 | 1 | 4 | 4 | 1 | 0 | 1 | 4 | 4 | 1 | 0 | 1 | 4 | 4 | 1 | 0 | 1 | 4 | 4 | 1 | 0 | 1 | 4 | 4 | 1 | 0 |
| mod 6 | 1 | 4 | 3 | 4 | 1 | 0 | 1 | 4 | 3 | 4 | 1 | 0 | 1 | 4 | 3 | 4 | 1 | 0 | 1 | 4 | 3 | 4 | 1 | 0 | 1 |
| mod 7 | 1 | 4 | 2 | 2 | 4 | 1 | 0 | 1 | 4 | 2 | 2 | 4 | 1 | 0 | 1 | 4 | 2 | 2 | 4 | 1 | 0 | 1 | 4 | 2 | 2 |
| mod 8 | 1 | 4 | 1 | 0 | 1 | 4 | 1 | 0 | 1 | 4 | 1 | 0 | 1 | 4 | 1 | 0 | 1 | 4 | 1 | 0 | 1 | 4 | 1 | 0 | 1 |
| mod 9 | 1 | 4 | 0 | 7 | 7 | 0 | 4 | 1 | 0 | 1 | 4 | 0 | 7 | 7 | 0 | 4 | 1 | 0 | 1 | 4 | 0 | 7 | 7 | 0 | 4 |
| mod 10 | 1 | 4 | 9 | 6 | 5 | 6 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 6 | 5 | 6 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 6 | 5 |
| mod 11 | 1 | 4 | 9 | 5 | 3 | 3 | 5 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 5 | 3 | 3 | 5 | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
| mod 12 | 1 | 4 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 4 | 1 | 0 | 1 |
| mod 13 | 1 | 4 | 9 | 3 | 12 | 10 | 10 | 12 | 3 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 3 | 12 | 10 | 10 | 12 | 3 | 9 | 4 | 1 |
| mod 14 | 1 | 4 | 9 | 2 | 11 | 8 | 7 | 8 | 11 | 2 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 2 | 11 | 8 | 7 | 8 | 11 | 2 | 9 |
| mod 15 | 1 | 4 | 9 | 1 | 10 | 6 | 4 | 4 | 6 | 10 | 1 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 1 | 10 | 6 | 4 | 4 | 6 | 10 |
| mod 16 | 1 | 4 | 9 | 0 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 0 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 0 | 9 | 4 | 1 | 0 | 1 |
| mod 17 | 1 | 4 | 9 | 16 | 8 | 2 | 15 | 13 | 13 | 15 | 2 | 8 | 16 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 | 8 | 2 | 15 | 13 |
| mod 18 | 1 | 4 | 9 | 16 | 7 | 0 | 13 | 10 | 9 | 10 | 13 | 0 | 7 | 16 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 | 7 | 0 | 13 |
| mod 19 | 1 | 4 | 9 | 16 | 6 | 17 | 11 | 7 | 5 | 5 | 7 | 11 | 17 | 6 | 16 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 | 6 | 17 |
| mod 20 | 1 | 4 | 9 | 16 | 5 | 16 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 | 5 | 16 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 | 5 |
| mod 21 | 1 | 4 | 9 | 16 | 4 | 15 | 7 | 1 | 18 | 16 | 16 | 18 | 1 | 7 | 15 | 4 | 16 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 |
| mod 22 | 1 | 4 | 9 | 16 | 3 | 14 | 5 | 20 | 15 | 12 | 11 | 12 | 15 | 20 | 5 | 14 | 3 | 16 | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
| mod 23 | 1 | 4 | 9 | 16 | 2 | 13 | 3 | 18 | 12 | 8 | 6 | 6 | 8 | 12 | 18 | 3 | 13 | 2 | 16 | 9 | 4 | 1 | 0 | 1 | 4 |
| mod 24 | 1 | 4 | 9 | 16 | 1 | 12 | 1 | 16 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 | 1 | 12 | 1 | 16 | 9 | 4 | 1 | 0 | 1 |
| mod 25 | 1 | 4 | 9 | 16 | 0 | 11 | 24 | 14 | 6 | 0 | 21 | 19 | 19 | 21 | 0 | 6 | 14 | 24 | 11 | 0 | 16 | 9 | 4 | 1 | 0 |
See also
- Euler's criterionEuler's criterionIn mathematics, Euler's criterion is used in determining in number theory whether a given integer is a quadratic residue modulo a prime.-Definition:Euler's criterion states:Let p be an odd prime and a an integer coprime to p. Then...
- Gauss's lemmaGauss's lemma (number theory)Gauss's lemma in number theory gives a condition for an integer to be a quadratic residue. Although it is not useful computationally, it has theoretical significance, being involved in some proofs of quadratic reciprocity....
- Zolotarev's lemmaZolotarev's lemmaIn number theory, Zolotarev's lemma states that the Legendre symbol\leftfor an integer a modulo an odd prime number p, where p does not divide a, can be computed as the sign of a permutation:...
- Character sumCharacter sumIn mathematics, a character sum is a sum\Sigma \chi\,of values of a Dirichlet character χ modulo N, taken over a given range of values of n. Such sums are basic in a number of questions, for example in the distribution of quadratic residues, and in particular in the classical question of finding an...
- Law of quadratic reciprocity
- Quadratic residue codeQuadratic residue codeA quadratic residue code is a type of cyclic code.There is a quadratic residue code of length pover the finite field GF whenever pand l are primes, p is odd andl is a quadratic residue modulo p....

