
Conference matrix
Encyclopedia
In mathematics
, a conference matrix (also called a C-matrix) is a square matrix
C with 0 on the diagonal and +1 and −1 off the diagonal, such that CTC is a multiple of the identity matrix
I. Thus, if the matrix has order n, CTC = (n−1)I.
Some authors use a more general definition, which requires there to be a single 0 in each row and column but not necessarily on the diagonal.
Conference matrices first arose in connection with a problem in telephony. They were first described by Vitold Belevitch
who also gave them their name. Belevitch was interested in constructing ideal telephone conference networks from ideal transformer
s and discovered that such networks were represented by conference matrices, hence the name. Other applications are in statistics
, and another is in elliptic geometry
.
For n > 1, there are two kinds of conference matrix. Let us normalize C by, first (if the more general definition is used), rearranging the rows so that all the zeros are on the diagonal, and then negating any row or column whose first entry is negative. (These operations do not change whether a matrix is a conference matrix.)
Thus, a normalized conference matrix has all 1's in its first row and column, except for a 0 in the top left corner, and is 0 on the diagonal. Let S be the matrix that remains when the first row and column of C are removed. Then either n is evenly even (a multiple of 4), and S is antisymmetric (as is the normalized C if its first row is negated), or n is oddly even (congruent to 2 modulo 4) and S is symmetric (as is the normalized C).
.
Given a symmetric conference matrix, the matrix S can be viewed as the Seidel adjacency matrix
of a graph
. The graph has n − 1 vertices, corresponding to the rows and columns of S, and two vertices are adjacent if the corresponding entry in S is negative. This graph is strongly regular
of the type called (after the matrix) a conference graph
.
The existence of conference matrices of orders n allowed by the above restrictions is known only for some values of n. For instance, if n = q + 1 where q is a prime power congruent to 1 (mod 4), then the Paley graph
s provide examples of symmetric conference matrices of order n, by taking S to be the Seidel matrix of the Paley graph.
The first few possible orders of a symmetric conference matrix are n = 2, 6, 10, 14, 18, (not 22, since 21 is not a sum of two squares), 26, 30, (not 34 since 33 is not a sum of two squares), 38, 42, 46, 50, 54, (not 58), 62 ; for every one of these, it is known that a symmetric conference matrix of that order exists. Order 66 seems to be an open problem.
conference matrix of order 6 is given by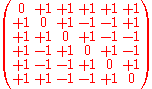 ,
,
all other conference matrices of order 6 are obtained from this one by flipping the signs of some row and/or column (and by taking permutations of rows and/or columns, according to the definition in use).
of order q which leads to an antisymmetric conference matrix of order n = q + 1. The matrix is obtained by taking for S the q × q matrix that has a +1 in position (i,j) and −1 in position (j,i) if there is an arc of the digraph from i to j, and zero diagonal. Then C constructed as above from S, but with the first row all negative, is an antisymmetric conference matrix.
This construction solves only a small part of the problem of deciding for which evenly even numbers n there exist antisymmetric conference matrices of order n.
W(n,w) is said to be of weight w>0 and order n if it is a square matrix of size n with entries from {−1, 0, +1} satisfying W Wt = w I. Using this definition, the zero element is no more required to be on the diagonal, but it is easy to see that still there must be exactly one zero element in each row and column. For example, the matrix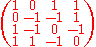
would satisfy this relaxed definition, but not the more strict one requiring the zero elements to be on the diagonal.
As mentioned above, a necessary condition for a conference matrix to exist is that n−1 must be the sum of two squares. Where there is more than one possible sum of two squares for n−1 there will exist multiple essentially different solutions for the corresponding conference network. This situation occurs at n of 26 and 66. The networks are particularly simple when n−1 is a perfect square (n = 2, 10, 26, …).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a conference matrix (also called a C-matrix) is a square matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
C with 0 on the diagonal and +1 and −1 off the diagonal, such that CTC is a multiple of the identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
I. Thus, if the matrix has order n, CTC = (n−1)I.
Some authors use a more general definition, which requires there to be a single 0 in each row and column but not necessarily on the diagonal.
Conference matrices first arose in connection with a problem in telephony. They were first described by Vitold Belevitch
Vitold Belevitch
Vitold Belevitch was a Belgian mathematician and electrical engineer of Russian extraction who produced some important work in the field of electrical network theory. Born to parents fleeing the Bolsheviks, he settled in Belgium where he worked on early computer construction projects...
who also gave them their name. Belevitch was interested in constructing ideal telephone conference networks from ideal transformer
Transformer
A transformer is a device that transfers electrical energy from one circuit to another through inductively coupled conductors—the transformer's coils. A varying current in the first or primary winding creates a varying magnetic flux in the transformer's core and thus a varying magnetic field...
s and discovered that such networks were represented by conference matrices, hence the name. Other applications are in statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, and another is in elliptic geometry
Elliptic geometry
Elliptic geometry is a non-Euclidean geometry, in which, given a line L and a point p outside L, there exists no line parallel to L passing through p. Elliptic geometry, like hyperbolic geometry, violates Euclid's parallel postulate, which can be interpreted as asserting that there is exactly one...
.
For n > 1, there are two kinds of conference matrix. Let us normalize C by, first (if the more general definition is used), rearranging the rows so that all the zeros are on the diagonal, and then negating any row or column whose first entry is negative. (These operations do not change whether a matrix is a conference matrix.)
Thus, a normalized conference matrix has all 1's in its first row and column, except for a 0 in the top left corner, and is 0 on the diagonal. Let S be the matrix that remains when the first row and column of C are removed. Then either n is evenly even (a multiple of 4), and S is antisymmetric (as is the normalized C if its first row is negated), or n is oddly even (congruent to 2 modulo 4) and S is symmetric (as is the normalized C).
Symmetric conference matrices
If C is a symmetric conference matrix of order n > 1, then not only must n be congruent to 2 (mod 4) but also n − 1 must be a sum of two square integers; there is a clever proof by elementary matrix theory in van Lint and Seidel. n will always be the sum of two squares if n − 1 is a prime powerPrime power
In mathematics, a prime power is a positive integer power of a prime number.For example: 5=51, 9=32 and 16=24 are prime powers, while6=2×3, 15=3×5 and 36=62=22×32 are not...
.
Given a symmetric conference matrix, the matrix S can be viewed as the Seidel adjacency matrix
Seidel adjacency matrix
In mathematics, in graph theory, the Seidel adjacency matrix of a simple graph G is the symmetric matrix with a row and column for each vertex, having 0 on the diagonal and, in the positions corresponding to vertices vi and vj, −1 if the vertices are adjacent...
of a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
. The graph has n − 1 vertices, corresponding to the rows and columns of S, and two vertices are adjacent if the corresponding entry in S is negative. This graph is strongly regular
Strongly regular graph
In graph theory, a discipline within mathematics, a strongly regular graph is defined as follows. Let G = be a regular graph with v vertices and degree k...
of the type called (after the matrix) a conference graph
Conference graph
In the mathematical area of graph theory, a conference graph is a strongly regular graph with parameters v, and It is the graph associated with a symmetric conference matrix, and consequently its order v must be 1 and a sum of two squares....
.
The existence of conference matrices of orders n allowed by the above restrictions is known only for some values of n. For instance, if n = q + 1 where q is a prime power congruent to 1 (mod 4), then the Paley graph
Paley graph
In mathematics, and specifically graph theory, Paley graphs, named after Raymond Paley, are dense undirected graphs constructed from the members of a suitable finite field by connecting pairs of elements that differ in a quadratic residue. The Paley graphs form an infinite family of conference...
s provide examples of symmetric conference matrices of order n, by taking S to be the Seidel matrix of the Paley graph.
The first few possible orders of a symmetric conference matrix are n = 2, 6, 10, 14, 18, (not 22, since 21 is not a sum of two squares), 26, 30, (not 34 since 33 is not a sum of two squares), 38, 42, 46, 50, 54, (not 58), 62 ; for every one of these, it is known that a symmetric conference matrix of that order exists. Order 66 seems to be an open problem.
Example
The essentially uniqueEssentially unique
In mathematics, the term essentially unique is used to indicate that while some object is not the only one that satisfies certain properties, all such objects are "the same" in some sense appropriate to the circumstances...
conference matrix of order 6 is given by
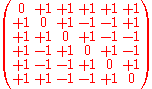 ,
,all other conference matrices of order 6 are obtained from this one by flipping the signs of some row and/or column (and by taking permutations of rows and/or columns, according to the definition in use).
Antisymmetric conference matrices
Antisymmetric conference matrices can also be produced by the Paley construction. Let q be a prime power with residue 3 (mod 4). Then there is a Paley digraphPaley graph
In mathematics, and specifically graph theory, Paley graphs, named after Raymond Paley, are dense undirected graphs constructed from the members of a suitable finite field by connecting pairs of elements that differ in a quadratic residue. The Paley graphs form an infinite family of conference...
of order q which leads to an antisymmetric conference matrix of order n = q + 1. The matrix is obtained by taking for S the q × q matrix that has a +1 in position (i,j) and −1 in position (j,i) if there is an arc of the digraph from i to j, and zero diagonal. Then C constructed as above from S, but with the first row all negative, is an antisymmetric conference matrix.
This construction solves only a small part of the problem of deciding for which evenly even numbers n there exist antisymmetric conference matrices of order n.
Generalizations
Sometimes a conference matrix of order n is just defined as a weighting matrix of the form W(n, n−1), whereW(n,w) is said to be of weight w>0 and order n if it is a square matrix of size n with entries from {−1, 0, +1} satisfying W Wt = w I. Using this definition, the zero element is no more required to be on the diagonal, but it is easy to see that still there must be exactly one zero element in each row and column. For example, the matrix
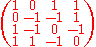
would satisfy this relaxed definition, but not the more strict one requiring the zero elements to be on the diagonal.
Telephone conference circuits
Belevitch obtained complete solutions for conference matrices for all values of n up to 38 and provided circuits for some of the smaller matrices. An ideal conference network is one where the loss of signal is entirely due to the signal being split between multiple conference subscriber ports. That is, there are no dissipation losses within the network. The network must contain ideal transformers only and no resistances. An n-port ideal conference network exists if and only if there exists a conference matrix of order n. For instance, a 3-port conference network can be constructed with the well-known hybrid transformer circuit used for 2-wire to 4-wire conversion in telephone handsets and line repeaters. However, there in no order 3 conference matrix and this circuit does not produce an ideal conference network. A resistance is needed for matching which dissipates signal, or else signal is lost through mismatch.As mentioned above, a necessary condition for a conference matrix to exist is that n−1 must be the sum of two squares. Where there is more than one possible sum of two squares for n−1 there will exist multiple essentially different solutions for the corresponding conference network. This situation occurs at n of 26 and 66. The networks are particularly simple when n−1 is a perfect square (n = 2, 10, 26, …).

