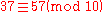Congruence relation
Encyclopedia
In abstract algebra
, a congruence relation (or simply congruence) is an equivalence relation
on an algebraic structure
(such as a group
, ring
, or vector space
) that is compatible with the structure. Every congruence relation has a corresponding quotient
structure, whose elements are the equivalence classes (or congruence classes) for the relation.
on the set of integer
s. For a given positive integer
, two integers 
and 
are called congruent modulo 
, written
if
is divisible by 
(or equivalently if 
and 
have the same remainder
when divided by
).
for example,
and 
are congruent modulo 
,
since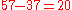
is a multiple of 10, or equivalently since both 
and 
have a remainder of 
when divided by 
.
Congruence modulo
(for a fixed 
) is compatible with both addition
and multiplication
on the integers. That is, if
then
The corresponding addition and multiplication of equivalence classes is known as modular arithmetic
. From the point of view of abstract algebra, congruence modulo
is a congruence relation on the ring
of integers, and arithmetic modulo
occurs on the corresponding quotient ring
.
under consideration. Particular definitions of congruence can be made for groups
, rings
, vector space
s, modules
, semigroup
s, lattices
, and so forth. The common theme is that a congruence is an equivalence relation
on an algebraic object that is compatible with the algebraic structure, in the sense that the operations
are well-defined
on the equivalence classes.
For example, a group is an algebraic object consisting of a set together with a single binary operation
, satisfying certain axioms. If
is a group with operation ∗, a congruence relation on G is an equivalence relation ≡ on the elements of G satisfying
for all g1, g2, h1, h2 ∈ G. For a congruence on a group, the equivalence class containing the identity element
is always a normal subgroup
, and the other equivalence classes are the coset
s of this subgroup. Together, these equivalence classes are the elements of a quotient group
.
When an algebraic structure includes more than one operation, congruence relations are required to be compatible with each operation. For example, a ring possesses both addition and multiplication, and a congruence relation on a ring must satisfy
whenever r1 ≡ r2 and s1 ≡ s2. For a congruence on a ring, the equivalence class containing 0 is always a two-sided ideal
, and the two operations on the set of equivalence classes define the corresponding quotient ring
.
The general notion of a congruence relation can be given a formal definition in the context of universal algebra
, a field which studies ideas common to all algebraic structures. In this setting, a congruence relation is an equivalence relation ≡ on an algebraic structure that satisfies
for every n-ary operation μ, and all elements a1,...,an,a1′,...,an′ satisfying ai ≡ ai′ for each i.
between two algebraic structures (such as homomorphism of groups
, or a linear map between vector space
s), then the relation ≡ defined by
is a congruence relation. By the first isomorphism theorem, the image
of A under ƒ is a substructure of B isomorphic
to the quotient of A by this congruence.
, congruence relations can be described in elementary terms as follows:
If G is a group (with identity element
e and operation *) and ~ is a binary relation
on G, then ~ is a congruence whenever:
Conditions 1, 2, and 3 say that ~ is an equivalence relation
.
A congruence ~ is determined entirely by the set {a ∈ G : a ~ e} of those elements of G that are congruent to the identity element, and this set is a normal subgroup
.
Specifically, a ~ b if and only if b−1 * a ~ e.
So instead of talking about congruences on groups, people usually speak in terms of normal subgroups of them; in fact, every congruence corresponds uniquely to some normal subgroup of G.
as ideals
instead of congruence relations, and in module theory
as submodules instead of congruence relations.
The most general situation where this trick is possible is in ideal-supporting algebras.
But this cannot be done with, for example, monoid
s, so the study of congruence relations plays a more central role in monoid theory.
:
A congruence relation on an algebra A is a subset
of the direct product
A × A that is both an equivalence relation
on A and a subalgebra
of A × A.
The kernel of a homomorphism
is always a congruence. Indeed, every congruence arises as a kernel.
For a given congruence ~ on A, the set A/~ of equivalence classes can be given the structure of an algebra in a natural fashion, the quotient algebra
.
The function that maps every element of A to its equivalence class is a homomorphism, and the kernel of this homomorphism is ~.
The lattice
Con(A) of all congruence relations on an algebra A is algebraic.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, a congruence relation (or simply congruence) is an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on an algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
(such as a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, or vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
) that is compatible with the structure. Every congruence relation has a corresponding quotient
Quotient
In mathematics, a quotient is the result of division. For example, when dividing 6 by 3, the quotient is 2, while 6 is called the dividend, and 3 the divisor. The quotient further is expressed as the number of times the divisor divides into the dividend e.g. The quotient of 6 and 2 is also 3.A...
structure, whose elements are the equivalence classes (or congruence classes) for the relation.
Basic example
The prototypical example of a congruence relation is congruence modulo on the set of integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s. For a given positive integer
, two integers and are called congruent modulo , written
if
is divisible by (or equivalently if and have the same remainderRemainder
In arithmetic, the remainder is the amount "left over" after the division of two integers which cannot be expressed with an integer quotient....
when divided by
).for example,
and are congruent modulo ,
since
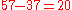is a multiple of 10, or equivalently since both and have a remainder of when divided by .Congruence modulo
(for a fixed ) is compatible with both additionAddition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
and multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
on the integers. That is, if
-
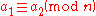and 
then
-
and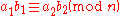 
The corresponding addition and multiplication of equivalence classes is known as modular arithmetic
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
. From the point of view of abstract algebra, congruence modulo
is a congruence relation on the ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
of integers, and arithmetic modulo
occurs on the corresponding quotient ringQuotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
.
Definition
The definition of a congruence depends on the type of algebraic structureAlgebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
under consideration. Particular definitions of congruence can be made for groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, rings
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s, modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
, semigroup
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
s, lattices
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
, and so forth. The common theme is that a congruence is an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on an algebraic object that is compatible with the algebraic structure, in the sense that the operations
Operation (mathematics)
The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
are well-defined
Well-defined
In mathematics, well-definition is a mathematical or logical definition of a certain concept or object which uses a set of base axioms in an entirely unambiguous way and satisfies the properties it is required to satisfy. Usually definitions are stated unambiguously, and it is clear they satisfy...
on the equivalence classes.
For example, a group is an algebraic object consisting of a set together with a single binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
, satisfying certain axioms. If
is a group with operation ∗, a congruence relation on G is an equivalence relation ≡ on the elements of G satisfying
- g1 ≡ g2 and h1 ≡ h2 ⇒ g1 ∗ h1 ≡ g2 ∗ h2
for all g1, g2, h1, h2 ∈ G. For a congruence on a group, the equivalence class containing the identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
is always a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
, and the other equivalence classes are the coset
Coset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
s of this subgroup. Together, these equivalence classes are the elements of a quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
.
When an algebraic structure includes more than one operation, congruence relations are required to be compatible with each operation. For example, a ring possesses both addition and multiplication, and a congruence relation on a ring must satisfy
- r1 + s1 ≡ r2 + s2 and r1s1 ≡ r2s2
whenever r1 ≡ r2 and s1 ≡ s2. For a congruence on a ring, the equivalence class containing 0 is always a two-sided ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
, and the two operations on the set of equivalence classes define the corresponding quotient ring
Quotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
.
The general notion of a congruence relation can be given a formal definition in the context of universal algebra
Universal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
, a field which studies ideas common to all algebraic structures. In this setting, a congruence relation is an equivalence relation ≡ on an algebraic structure that satisfies
- μ(a1, a2, ..., an) ≡ μ(a1′, a2′, ..., an′)
for every n-ary operation μ, and all elements a1,...,an,a1′,...,an′ satisfying ai ≡ ai′ for each i.
Relation with homomorphisms
If ƒ: A → B is a homomorphismHomomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
between two algebraic structures (such as homomorphism of groups
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
, or a linear map between vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s), then the relation ≡ defined by
- a1 ≡ a2 if and only if ƒ(a1) = ƒ(a2)
is a congruence relation. By the first isomorphism theorem, the image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of A under ƒ is a substructure of B isomorphic
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
to the quotient of A by this congruence.
Congruences of groups, and normal subgroups and ideals
In the particular case of groupsGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, congruence relations can be described in elementary terms as follows:
If G is a group (with identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
e and operation *) and ~ is a binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
on G, then ~ is a congruence whenever:
- Given any element a of G, a ~ a (reflexivityReflexive relationIn mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
); - Given any elements a and b of G, if a ~ b, then b ~ a (symmetrySymmetric relationIn mathematics, a binary relation R over a set X is symmetric if it holds for all a and b in X that if a is related to b then b is related to a.In mathematical notation, this is:...
); - Given any elements a, b, and c of G, if a ~ b andLogical conjunctionIn logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
b ~ c, then a ~ c (transitivityTransitive relationIn mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
); - Given any elements a, a' , b, and b' of G, if a ~ a' and b ~ b' , then a * b ~ a' * b' ;
- Given any elements a and a' of G, if a ~ a' , then a−1 ~ a' −1 (this can actually be proven from the other four, so is strictly redundant).
Conditions 1, 2, and 3 say that ~ is an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
.
A congruence ~ is determined entirely by the set {a ∈ G : a ~ e} of those elements of G that are congruent to the identity element, and this set is a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
.
Specifically, a ~ b if and only if b−1 * a ~ e.
So instead of talking about congruences on groups, people usually speak in terms of normal subgroups of them; in fact, every congruence corresponds uniquely to some normal subgroup of G.
Ideals of rings and the general case of kernels
A similar trick allows one to speak of kernels in ring theoryRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
as ideals
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
instead of congruence relations, and in module theory
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
as submodules instead of congruence relations.
The most general situation where this trick is possible is in ideal-supporting algebras.
But this cannot be done with, for example, monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
s, so the study of congruence relations plays a more central role in monoid theory.
Universal algebra
The idea is generalized in universal algebraUniversal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
:
A congruence relation on an algebra A is a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of the direct product
Direct product
In mathematics, one can often define a direct product of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets, together with a suitably defined structure on the product set....
A × A that is both an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on A and a subalgebra
Subalgebra
In mathematics, the word "algebra", when referring to a structure, often means a vector space or module equipped with an additional bilinear operation. Algebras in universal algebra are far more general: they are a common generalisation of all algebraic structures...
of A × A.
The kernel of a homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
is always a congruence. Indeed, every congruence arises as a kernel.
For a given congruence ~ on A, the set A/~ of equivalence classes can be given the structure of an algebra in a natural fashion, the quotient algebra
Quotient algebra
In mathematics, a quotient algebra, , also called a factor algebra is obtained by partitioning the elements of an algebra in equivalence classes given by a congruence, that is an equivalence relation that is additionally compatible with all the operations of the algebra, in the formal sense...
.
The function that maps every element of A to its equivalence class is a homomorphism, and the kernel of this homomorphism is ~.
The lattice
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
Con(A) of all congruence relations on an algebra A is algebraic.