
Pseudoconvexity
Encyclopedia
In mathematics
, more precisely in the theory of functions of several complex variables
, a pseudoconvex set is a special type of open set
in the n-dimensional complex space Cn. Pseudoconvex sets are important, as they allow for classification of domains of holomorphy
.
Let
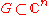
be a domain, that is, an open
connected
subset
. One says that is pseudoconvex (or Hartogs
is pseudoconvex (or Hartogs
pseudoconvex) if there exists a continuous
plurisubharmonic function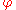 on
on  such that the set
such that the set
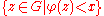
is a relatively compact subset of for all real number
for all real number
s In other words, a domain is pseudoconvex if
In other words, a domain is pseudoconvex if  has a continuous plurisubharmonic exhaustion function. Every (geometrically) convex set
has a continuous plurisubharmonic exhaustion function. Every (geometrically) convex set
is pseudoconvex.
When has a
has a 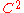 (twice continuously differentiable
(twice continuously differentiable
) boundary
, this notion is the same as Levi pseudoconvexity, which is easier to work with. More specifically, with a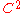 boundary, it can be shown that
boundary, it can be shown that  has a defining function; ie., that there exists
has a defining function; ie., that there exists 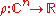 which is
which is 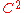 so that
so that 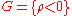 , and
, and 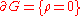 . Now,
. Now,  is pseudoconvex iff for every
is pseudoconvex iff for every 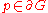 and
and  in the complex tangent space at p that is,
in the complex tangent space at p that is,
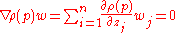 we have
we have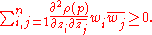
If does not have a
does not have a 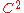 boundary, the following approximation result can come in useful.
boundary, the following approximation result can come in useful.
Proposition 1 If is pseudoconvex, then there exist bounded
is pseudoconvex, then there exist bounded
, strongly Levi pseudoconvex domains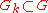 with
with 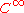 (smooth
(smooth
) boundary which are relatively compact in , such that
, such that
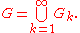
This is because once we have a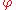 as in the definition we can actually find a C∞ exhaustion function.
as in the definition we can actually find a C∞ exhaustion function.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, more precisely in the theory of functions of several complex variables
Several complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
, a pseudoconvex set is a special type of open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
in the n-dimensional complex space Cn. Pseudoconvex sets are important, as they allow for classification of domains of holomorphy
Domain of holomorphy
In mathematics, in the theory of functions of several complex variables, a domain of holomorphy is a set which is maximal in the sense that there exists a holomorphic function on this set which cannot be extended to a bigger set....
.
Let
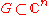
be a domain, that is, an open
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
. One says that
 is pseudoconvex (or Hartogs
is pseudoconvex (or HartogsFriedrich Hartogs
Friedrich Moritz Hartogs was a German-Jewish mathematician, known for work on set theory and foundational results on several complex variables.- See also :*Hartogs domain*Hartogs–Laurent expansion...
pseudoconvex) if there exists a continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
plurisubharmonic function
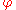 on
on  such that the set
such that the set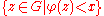
is a relatively compact subset of
 for all real number
for all real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s
 In other words, a domain is pseudoconvex if
In other words, a domain is pseudoconvex if  has a continuous plurisubharmonic exhaustion function. Every (geometrically) convex set
has a continuous plurisubharmonic exhaustion function. Every (geometrically) convex setConvex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
is pseudoconvex.
When
 has a
has a 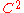 (twice continuously differentiable
(twice continuously differentiableSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
) boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
, this notion is the same as Levi pseudoconvexity, which is easier to work with. More specifically, with a
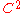 boundary, it can be shown that
boundary, it can be shown that  has a defining function; ie., that there exists
has a defining function; ie., that there exists 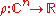 which is
which is 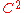 so that
so that 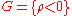 , and
, and 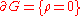 . Now,
. Now,  is pseudoconvex iff for every
is pseudoconvex iff for every 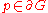 and
and  in the complex tangent space at p that is,
in the complex tangent space at p that is,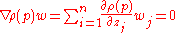 we have
we have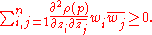
If
 does not have a
does not have a 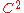 boundary, the following approximation result can come in useful.
boundary, the following approximation result can come in useful.Proposition 1 If
 is pseudoconvex, then there exist bounded
is pseudoconvex, then there exist boundedBounded set
In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
, strongly Levi pseudoconvex domains
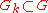 with
with 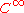 (smooth
(smoothSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
) boundary which are relatively compact in
 , such that
, such that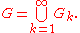
This is because once we have a
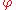 as in the definition we can actually find a C∞ exhaustion function.
as in the definition we can actually find a C∞ exhaustion function.
