
Domain of holomorphy
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the theory of functions of several complex variables
Several complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
, a domain of holomorphy is a set which is maximal in the sense that there exists a holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
on this set which cannot be extended
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
to a bigger set.
Formally, an open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
 in the n-dimensional complex space
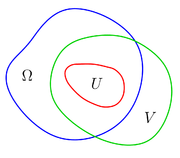
in the n-dimensional complex space 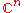 is called a domain of holomorphy if there do not exist non-empty open sets
is called a domain of holomorphy if there do not exist non-empty open sets  and
and 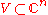 where
where  is connected
is connectedConnected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
,
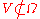 and
and  such that for every holomorphic function
such that for every holomorphic function  on
on  there exists a holomorphic function
there exists a holomorphic function 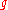 on
on  with
with  on
on 
In the
 case, every open set is a domain of holomorphy: we can define a holomorphic function with zeros accumulating everywhere on the boundary
case, every open set is a domain of holomorphy: we can define a holomorphic function with zeros accumulating everywhere on the boundaryBoundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of the domain, which must then be a natural boundary for a domain of definition of its inverse. For
 this is no longer true, as it follows from Hartogs' lemma.
this is no longer true, as it follows from Hartogs' lemma.Equivalent conditions
For a domain the following conditions are equivalent:
the following conditions are equivalent:
-
 is a domain of holomorphy
is a domain of holomorphy -
 is holomorphically convexHolomorphically convex hullIn mathematics, more precisely in complex analysis, the holomorphically convex hull of a given compact set in the n-dimensional complex space Cn is defined as follows....
is holomorphically convexHolomorphically convex hullIn mathematics, more precisely in complex analysis, the holomorphically convex hull of a given compact set in the n-dimensional complex space Cn is defined as follows.... -
 is pseudoconvex
is pseudoconvex -
 is Levi convex - for every sequence
is Levi convex - for every sequence  of analytic compact surfaces such that
of analytic compact surfaces such that 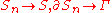 for some set
for some set  we have
we have  (
(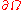 cannot be "touched from inside" by a sequence of analytic surfaces)
cannot be "touched from inside" by a sequence of analytic surfaces) -
 has local Levi property - for every point
has local Levi property - for every point 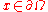 there exist a neighbourhood
there exist a neighbourhood  of
of  and
and  holomorphic on
holomorphic on  such that
such that  cannot be extended to any neighbourhood of
cannot be extended to any neighbourhood of 
Implications
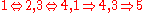 are standard results. The main difficulty lies in proving
are standard results. The main difficulty lies in proving  , i.e. constructing a global holomoprhic function which admits no extension from non-extendable functions defined only locally. This is called the Levi problem and was first solved by Kiyoshi Oka
, i.e. constructing a global holomoprhic function which admits no extension from non-extendable functions defined only locally. This is called the Levi problem and was first solved by Kiyoshi OkaKiyoshi Oka
was a Japanese mathematician who did fundamental work in the theory of several complex variables. He was born in Osaka. He went to Kyoto Imperial University in 1919, turning to mathematics in 1923 and graduating in 1924....
, and then by Lars Hörmander
Lars Hörmander
Lars Valter Hörmander is a Swedish mathematician who has been called "the foremost contributor to the modern theory of linear partial differential equations". He was awarded the Fields Medal in 1962, and the Wolf Prize in 1988...
using methods from functional analysis and partial differential equations (a consequence of
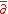 -problem).
-problem).Properties
- if
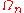 are domains of holomorphy, then their intersection
are domains of holomorphy, then their intersection 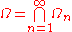 is also a domain of holomorphy
is also a domain of holomorphy - if
 is an ascending sequence of domains of holomorphy, then their union
is an ascending sequence of domains of holomorphy, then their union  is also a domain of holomorphy (see Behnke-Stein theorem)
is also a domain of holomorphy (see Behnke-Stein theorem) - product
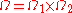 of domains of holomorphy
of domains of holomorphy  is a domain of holomorphy
is a domain of holomorphy - the first Cousin problemCousin problemsIn mathematics, the Cousin problems are two questions in several complex variables, concerning the existence of meromorphic functions that are specified in terms of local data. They were introduced in special cases by P. Cousin in 1895...
is always solvable in a domain of holomorphy; this is also true, with additional topological assumptions, for the second Cousin problemCousin problemsIn mathematics, the Cousin problems are two questions in several complex variables, concerning the existence of meromorphic functions that are specified in terms of local data. They were introduced in special cases by P. Cousin in 1895...
See also
- Behnke–Stein theoremBehnke–Stein theoremIn mathematics, especially several complex variables, the Behnke–Stein theorem states that a union of an increasing sequence G_k of domains of holomorphy is again a domain of holomorphy....
- Levi pseudoconvex
- solution of the Levi problem
----

