Projected dynamical system
Encyclopedia
Projected dynamical systems is a mathematical
theory investigating the behaviour of dynamical system
s where solutions are restricted to a constraint set. The discipline shares connections to and applications with both the static world of optimization
and equilibrium problems and the dynamical world of ordinary differential equations. A projected dynamical system is given by the flow
to the projected differential equation
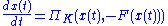
where K is our constraint set. Differential equations of this form are notable for having a discontinuous vector field.
modeling, convex
polyhedral
sets in operations research
, etc. One particularly important class of equilibrium problems which has aided in the rise of projected dynamical systems has been that of variational inequalities
.
The formalization of projected dynamical systems began in the 1990s. However, similar concepts can be found in the mathematical literature which predate this, especially in connection with variational inequalities and differential inclusions.
s. Here we take K to be a closed
, convex
subset of some Hilbert space
X.
The normal cone to the set K at the point x in K is given by
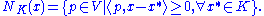
The tangent cone (or contingent cone) to the set K at the point x is given by
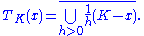
The projection operator (or closest element mapping) of a point x in X to K is given by the point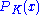
in K such that
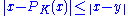
for every y in K.
The vector projection operator of a vector v in X at a point x in K is given by
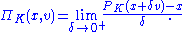
On the interior
of K solutions behave as they would if the system were an unconstrained ordinary differential equation. However, since the vector field is discontinuous along the boundary of the set, projected differential equations belong to the class of discontinuous ordinary differential equations. While this makes much of ordinary differential equation theory inapplicable, it is known that when -F is a Lipschitz
continuous vector field, a unique absolutely continuous solution exists through each initial point x(0)=x0 in K on the interval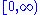
.
This differential equation can be alternately characterized by
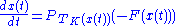
or
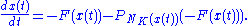
The convention of denoting the vector field -F with a negative sign arises from a particular connection projected dynamical systems shares with variational inequalities. The convention in the literature is to refer to the vector field as positive in the variational inequality, and negative in the corresponding projected dynamical system.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
theory investigating the behaviour of dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
s where solutions are restricted to a constraint set. The discipline shares connections to and applications with both the static world of optimization
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
and equilibrium problems and the dynamical world of ordinary differential equations. A projected dynamical system is given by the flow
Flow (mathematics)
In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...
to the projected differential equation
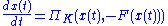
where K is our constraint set. Differential equations of this form are notable for having a discontinuous vector field.
History of projected dynamical systems
Projected dynamical systems have evolved out of the desire to dynamically model the behaviour of nonstatic solutions in equilibrium problems over some parameter, typically take to be time. This dynamics differs from that of ordinary differential equations in that solutions are still restricted to whatever constraint set the underlying equilibrium problem was working on, e.g. nonnegativity of investments in financialFinance
"Finance" is often defined simply as the management of money or “funds” management Modern finance, however, is a family of business activity that includes the origination, marketing, and management of cash and money surrogates through a variety of capital accounts, instruments, and markets created...
modeling, convex
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
polyhedral
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
sets in operations research
Operations research
Operations research is an interdisciplinary mathematical science that focuses on the effective use of technology by organizations...
, etc. One particularly important class of equilibrium problems which has aided in the rise of projected dynamical systems has been that of variational inequalities
Variational inequality
In mathematics, a variational inequality is an inequality involving a functional, which has to be solved for all the value of a given variable, belonging usually to a convex set...
.
The formalization of projected dynamical systems began in the 1990s. However, similar concepts can be found in the mathematical literature which predate this, especially in connection with variational inequalities and differential inclusions.
Projections and Cones
Any solution to our projected differential equation must remain inside of our constraint set K for all time. This desired result is achieved through the use of projection operators and two particular important classes of convex coneConvex cone
In linear algebra, a convex cone is a subset of a vector space over an ordered field that is closed under linear combinations with positive coefficients.-Definition:...
s. Here we take K to be a closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
, convex
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
subset of some Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
X.
The normal cone to the set K at the point x in K is given by
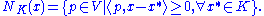
The tangent cone (or contingent cone) to the set K at the point x is given by
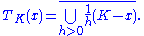
The projection operator (or closest element mapping) of a point x in X to K is given by the point
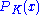in K such that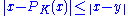for every y in K.
The vector projection operator of a vector v in X at a point x in K is given by
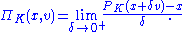
Projected Differential Equations
Given a closed, convex subset K of a Hilbert space X and a vector field -F which takes elements from K into X, the projected differential equation associated with K and -F is defined to beOn the interior
Interior (topology)
In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
of K solutions behave as they would if the system were an unconstrained ordinary differential equation. However, since the vector field is discontinuous along the boundary of the set, projected differential equations belong to the class of discontinuous ordinary differential equations. While this makes much of ordinary differential equation theory inapplicable, it is known that when -F is a Lipschitz
Lipschitz
- People :Lipschitz is a surname, which may be derived from the Polish city of Głubczyce , and may refer to:* Daniel Lipšic, Minister of Interior in Slovakia* Dr...
continuous vector field, a unique absolutely continuous solution exists through each initial point x(0)=x0 in K on the interval
.This differential equation can be alternately characterized by
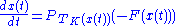
or
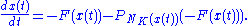
The convention of denoting the vector field -F with a negative sign arises from a particular connection projected dynamical systems shares with variational inequalities. The convention in the literature is to refer to the vector field as positive in the variational inequality, and negative in the corresponding projected dynamical system.
See also
- Differential variational inequalityDifferential variational inequalityIn mathematics, a differential variational inequality is a dynamical system that incorporates ordinary differential equations and variational inequalities or complementarity problems. DVIs are useful for representing models involving both dynamics and inequality constraints...
- Dynamical systems theoryDynamical systems theoryDynamical systems theory is an area of applied mathematics used to describe the behavior of complex dynamical systems, usually by employing differential equations or difference equations. When differential equations are employed, the theory is called continuous dynamical systems. When difference...
- Ordinary differential equationOrdinary differential equationIn mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
- Variational inequalityVariational inequalityIn mathematics, a variational inequality is an inequality involving a functional, which has to be solved for all the value of a given variable, belonging usually to a convex set...
- Differential inclusion
- Complementarity theoryComplementarity theoryA complementarity problem is a type of mathematical optimization problem. It is the problem of optimizing a function of two vector variables subject to certain requirements which include: that the inner product of the two variables must equal zero, i.e. = 0...