Photon dynamics in the double-slit experiment
Encyclopedia
The dynamics of photons in the double-slit experiment describes the relationship between classical electromagnetic waves and photon
s, the quantum counterpart of classical electromagnetic waves, in the context of the double-slit experiment
.
s are a simplified version of Maxwell's equations
which describe the propagation of electromagnetic waves through a medium
or in a vacuum
. The homogeneous
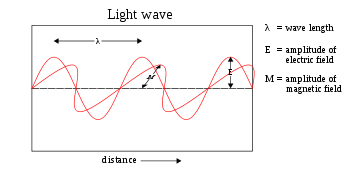
form of the equation, written in terms of either the electric field
E or the magnetic field
B, takes the form:


where c is the speed of light
in the medium. In a vacuum, c = 2.998 x 108 meters per second, which is the speed of light in free space.
The magnetic field is related to the electric field through the Maxwell correction to Ampere's Law
 .
.
solution for an electromagnetic wave
traveling in the z direction is (cgs units and SI units)

for the electric field and

for the magnetic field, where k is the wavenumber
,

is the angular frequency
of the wave, and is the speed of light
is the speed of light
. The hats on the vectors indicate unit vectors in the x, y, and z directions.
 The plane wave is parameterized by the amplitude
The plane wave is parameterized by the amplitude
s


and phases

where
 .
.
and
 .
.
The solution can be written concisely as

where

is the Jones vector in the x-y plane. The notation for this vector is the bra-ket notation
of Dirac
, which is normally used in a quantum context. The quantum notation is used here in anticipation of the interpretation of the Jones vector as a quantum state vector.

where is the distance from the origin and
is the distance from the origin and  is some distance from the origin at which the electric field
is some distance from the origin at which the electric field  is measured.
is measured.
Again, the magnetic field is related to the electric field by

where the unit vector is in the radial direction.


where is now the distance from the line. This solution falls off as the square root of distance while the spherical solution falls off as the distance.
is now the distance from the line. This solution falls off as the square root of distance while the spherical solution falls off as the distance.
 Huygen's principle states that each point of an advancing wave front is in fact the center of a fresh disturbance and the source of a new train of waves; and that the advancing wave as a whole may be regarded as the sum of all the secondary waves arising from points in the medium already traversed.
Huygen's principle states that each point of an advancing wave front is in fact the center of a fresh disturbance and the source of a new train of waves; and that the advancing wave as a whole may be regarded as the sum of all the secondary waves arising from points in the medium already traversed.
This means that a plane wave impinging on two nearby slits in a barrier can be thought of as two coherent sources of light emanating from each of the slits. If the slits are very long compared with the distance at which the waves are observed, then the waves are cylindrical waves. If the slits are very short compared with the distance they are observed, then the waves are spherical waves. In either case the electric field for the wave emanating from each slit is proportional to
 .
.
 Consider two slits separated by a distance d. Place a screen a distance L from the slits. The distance from slit 1 to a point x on the screen is
Consider two slits separated by a distance d. Place a screen a distance L from the slits. The distance from slit 1 to a point x on the screen is

and the distance from slit 2 to the point x on the screen is
 .
.
For large L and small x compared with L, the difference between the two distances is approximately
 .
.
The electric field at point x is given by the superposition of the states of the waves from each of the slits and is proportional to the real part of

 The total electromagnetic energy striking the screen at point x is proportional to the square of the electric field and is therefore proportional to
The total electromagnetic energy striking the screen at point x is proportional to the square of the electric field and is therefore proportional to

where is the wavelength
is the wavelength
of the light. The fields from the two slits constructively interfere and form antinodes
when the phase is equal to multiples of

or
 .
.
The waves destructively interfere and form nodes
halfway in between the antinodes.
semi-classical photoelectric effecthttp://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19680009569_1968009569.pdf.
. It is a testament, however, to the generality of Maxwell's equations
for electrodynamics that the treatment can be made quantum mechanical
with only a reinterpretation of classical quantities. The reinterpretation is that the state vectors

in the classical description of the double-slit experiment become quantum state vectors in the description of photons.
and the interpretation of those experiments by Albert Einstein
.
The important conclusion from these early experiments is that electromagnetic radiation is composed of irreducible packets of energy, known as photon
s.
 of each packet is related to the angular frequency
of each packet is related to the angular frequency  of the wave by the relation
of the wave by the relation

where is an experimentally determined quantity known as Planck's constant divided by 2 pi.
is an experimentally determined quantity known as Planck's constant divided by 2 pi.
If there are photons in a box of volume
photons in a box of volume  , the energy in the electromagnetic field is
, the energy in the electromagnetic field is

and the energy density
is

The energy of a photon can be related to classical fields through the correspondence principle
which states that for a large number of photons, the quantum and classical treatments must agree. Thus, for very large , the quantum energy density must be the same as the classical energy density (complex notation, cgs units)
, the quantum energy density must be the same as the classical energy density (complex notation, cgs units)
 .
.
The number of photons in the box is then
 .
.
 The correspondence principle also determines the momentum of the photon. The momentum density
The correspondence principle also determines the momentum of the photon. The momentum density
is

which implies that the momentum of a photon (see Matter wave ) is
 .
.
(since and
and  this reduces to
this reduces to 
as defined in quantum optics.
Dirac explains the situation in terms of one photon, although this was well before our modern understanding of quantum optics
. For the double-slit experiment
:
is related to the expectation value of the energy density of the equivalent E and B fields.
In general, the rule for combining probability amplitudes look very much like the classical rules for composition of probabilities:[The following quote is from Baym, Chapter 1]
with only a reinterpretation of the classical field as a probability amplitude for the photon, however this notion is fraught with danger and ultimately leads to contradictions. One should not simply assume that the electromagnetic fields are a wave-function for the photon. For one thing, they are real and thus contain both positive and negative frequency components, which cannot be reconciled with the requirement for Schroedinger wavefunctions which are complex, positive frequency only. In addition, the electromagnetic fields are observable (e.g. with an oscilloscope) while Schroedinger wavefunctions are not observable, even in principle. Clearly, then, the fields are not wavefunctions, are physical, observable fields, rather than merely what you take the modulus-square of to obtain the probability of finding a photon somewhere. The existence of some "wavefunction of the photon" is not a fully settled issue.http://adsabs.harvard.edu/abs/2005quant.ph..8202B
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
s, the quantum counterpart of classical electromagnetic waves, in the context of the double-slit experiment
Double-slit experiment
The double-slit experiment, sometimes called Young's experiment, is a demonstration that matter and energy can display characteristics of both waves and particles...
.
Electromagnetic wave equations
The electromagnetic wave equationElectromagnetic wave equation
The electromagnetic wave equation is a second-order partial differential equation that describes the propagation of electromagnetic waves through a medium or in a vacuum...
s are a simplified version of Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
which describe the propagation of electromagnetic waves through a medium
Medium (optics)
An optical medium is material through which electromagnetic waves propagate. It is a form of transmission medium. The permittivity and permeability of the medium define how electromagnetic waves propagate in it...
or in a vacuum
Vacuum
In everyday usage, vacuum is a volume of space that is essentially empty of matter, such that its gaseous pressure is much less than atmospheric pressure. The word comes from the Latin term for "empty". A perfect vacuum would be one with no particles in it at all, which is impossible to achieve in...
. The homogeneous
Homogeneous differential equation
The term homogeneous differential equation has several distinct meanings.One meaning is that a first-order ordinary differential equation is homogeneous if it has the formwhere F is a homogeneous function of degree zero; that is to say, that F = F.In a related, but distinct, usage, the term linear...
form of the equation, written in terms of either the electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
E or the magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
B, takes the form:


where c is the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
in the medium. In a vacuum, c = 2.998 x 108 meters per second, which is the speed of light in free space.
The magnetic field is related to the electric field through the Maxwell correction to Ampere's Law
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
 .
.Plane wave solution of the electromagnetic wave equation
The plane sinusoidalSine wave
The sine wave or sinusoid is a mathematical function that describes a smooth repetitive oscillation. It occurs often in pure mathematics, as well as physics, signal processing, electrical engineering and many other fields...
solution for an electromagnetic wave
Electromagnetic wave equation
The electromagnetic wave equation is a second-order partial differential equation that describes the propagation of electromagnetic waves through a medium or in a vacuum...
traveling in the z direction is (cgs units and SI units)

for the electric field and

for the magnetic field, where k is the wavenumber
Wavenumber
In the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector...
,

is the angular frequency
Angular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
of the wave, and
 is the speed of light
is the speed of lightSpeed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
. The hats on the vectors indicate unit vectors in the x, y, and z directions.

Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
s


and phases
Phase (waves)
Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...

where
 .
.and
 .
.The solution can be written concisely as

where

is the Jones vector in the x-y plane. The notation for this vector is the bra-ket notation
Bra-ket notation
Bra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...
of Dirac
Paul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
, which is normally used in a quantum context. The quantum notation is used here in anticipation of the interpretation of the Jones vector as a quantum state vector.
Spherical waves
The solution for spherical waves emanating from the origin is
where
 is the distance from the origin and
is the distance from the origin and  is some distance from the origin at which the electric field
is some distance from the origin at which the electric field  is measured.
is measured.Again, the magnetic field is related to the electric field by

where the unit vector is in the radial direction.
Cylindrical waves
The cylindrical solutions of the wave equation for waves emanating from an infinitely long line are Bessel functions. For large distances from the line, the solution reduces to

where
 is now the distance from the line. This solution falls off as the square root of distance while the spherical solution falls off as the distance.
is now the distance from the line. This solution falls off as the square root of distance while the spherical solution falls off as the distance.Huygens' principle

This means that a plane wave impinging on two nearby slits in a barrier can be thought of as two coherent sources of light emanating from each of the slits. If the slits are very long compared with the distance at which the waves are observed, then the waves are cylindrical waves. If the slits are very short compared with the distance they are observed, then the waves are spherical waves. In either case the electric field for the wave emanating from each slit is proportional to
 .
.Interference


and the distance from slit 2 to the point x on the screen is
 .
.For large L and small x compared with L, the difference between the two distances is approximately
 .
.The electric field at point x is given by the superposition of the states of the waves from each of the slits and is proportional to the real part of



where
 is the wavelength
is the wavelengthWavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
of the light. The fields from the two slits constructively interfere and form antinodes
Node (physics)
A node is a point along a standing wave where the wave has minimal amplitude. For instance, in a vibrating guitar string, the ends of the string are nodes. By changing the position of the end node through frets, the guitarist changes the effective length of the vibrating string and thereby the...
when the phase is equal to multiples of


or
 .
.The waves destructively interfere and form nodes
Node (physics)
A node is a point along a standing wave where the wave has minimal amplitude. For instance, in a vibrating guitar string, the ends of the string are nodes. By changing the position of the end node through frets, the guitarist changes the effective length of the vibrating string and thereby the...
halfway in between the antinodes.
Semi-classical description of the double-slit experiment
It is possible to explain why a photographic film darkens in "spots" at very low light intensities while keeping the electromagnetic field classical (described by the Maxwell equations). In order to get quantitavely correct results, the electrons in the photographic plate or screen must be treated according to the Schroedinger equation of quantum mechanics. Because the atoms in the screen or photographic plate are treated quantum-mechanically but the light treated classically, such analyses are said to be semi-classical. This type of reasoning predicts the correct results when thermal light sources are used, and follows the same lines as thesemi-classical photoelectric effecthttp://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19680009569_1968009569.pdf.
Quantum description of the double-slit experiment
The treatment to this point has been classicalClassical physics
What "classical physics" refers to depends on the context. When discussing special relativity, it refers to the Newtonian physics which preceded relativity, i.e. the branches of physics based on principles developed before the rise of relativity and quantum mechanics...
. It is a testament, however, to the generality of Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
for electrodynamics that the treatment can be made quantum mechanical
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
with only a reinterpretation of classical quantities. The reinterpretation is that the state vectors

in the classical description of the double-slit experiment become quantum state vectors in the description of photons.
Energy and momentum of photons
The reinterpretation is based on the experiments of Max PlanckMax Planck
Max Karl Ernst Ludwig Planck, ForMemRS, was a German physicist who actualized the quantum physics, initiating a revolution in natural science and philosophy. He is regarded as the founder of the quantum theory, for which he received the Nobel Prize in Physics in 1918.-Life and career:Planck came...
and the interpretation of those experiments by Albert Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
.
The important conclusion from these early experiments is that electromagnetic radiation is composed of irreducible packets of energy, known as photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
s.
Energy
The energy of each packet is related to the angular frequency
of each packet is related to the angular frequency  of the wave by the relation
of the wave by the relation
where
 is an experimentally determined quantity known as Planck's constant divided by 2 pi.
is an experimentally determined quantity known as Planck's constant divided by 2 pi.If there are
 photons in a box of volume
photons in a box of volume  , the energy in the electromagnetic field is
, the energy in the electromagnetic field is
and the energy density
Energy density
Energy density is a term used for the amount of energy stored in a given system or region of space per unit volume. Often only the useful or extractable energy is quantified, which is to say that chemically inaccessible energy such as rest mass energy is ignored...
is

The energy of a photon can be related to classical fields through the correspondence principle
Correspondence principle
In physics, the correspondence principle states that the behavior of systems described by the theory of quantum mechanics reproduces classical physics in the limit of large quantum numbers....
which states that for a large number of photons, the quantum and classical treatments must agree. Thus, for very large
 , the quantum energy density must be the same as the classical energy density (complex notation, cgs units)
, the quantum energy density must be the same as the classical energy density (complex notation, cgs units) .
.The number of photons in the box is then
 .
.Momentum

Poynting vector
In physics, the Poynting vector can be thought of as representing the directional energy flux density of an electromagnetic field. It is named after its inventor John Henry Poynting. Oliver Heaviside and Nikolay Umov independently co-invented the Poynting vector...
is

which implies that the momentum of a photon (see Matter wave ) is
 .
.(since
 and
and  this reduces to
this reduces to 
Probability for a single photon
There are two ways in which probability can be applied to the behavior of photons; probability can be used to calculate the probable number of photons in a particular state, or probability can be used to calculate the likelihood of a single photon to be in a particular state. The former interpretation is applicable for coherent states and statistical mixtures of such, as thermal light, while the latter is to be used for a single-photon Fock stateFock state
A Fock state , in quantum mechanics, is any element of a Fock space with a well-defined number of particles . These states are named after the Soviet physicist, V. A. Fock.-Definition:...
as defined in quantum optics.
Dirac explains the situation in terms of one photon, although this was well before our modern understanding of quantum optics
Quantum optics
Quantum optics is a field of research in physics, dealing with the application of quantum mechanics to phenomena involving light and its interactions with matter.- History of quantum optics :...
. For the double-slit experiment
Double-slit experiment
The double-slit experiment, sometimes called Young's experiment, is a demonstration that matter and energy can display characteristics of both waves and particles...
:
Probability amplitudes
The probability for a photon to be in a particular polarization state depends on the fields as calculated by the classical Maxwell's equations. The photon probability density of a single-photon Fock stateFock state
A Fock state , in quantum mechanics, is any element of a Fock space with a well-defined number of particles . These states are named after the Soviet physicist, V. A. Fock.-Definition:...
is related to the expectation value of the energy density of the equivalent E and B fields.
In general, the rule for combining probability amplitudes look very much like the classical rules for composition of probabilities:[The following quote is from Baym, Chapter 1]
- The probability amplitude for two successive probabilities is the product of amplitudes for the individual possibilities. ...
- The amplitude for a process that can take place in one of several indistinguishable ways is the sum of amplitudes for each of the individual ways. ...
- The total probability for the process to occur is the absolute value squared of the total amplitude calculated by 1 and 2.
Wave function of the photon
Superficially, it may look like the dynamics of a photon can be completely described by the classical Maxwell's equationsMaxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
with only a reinterpretation of the classical field as a probability amplitude for the photon, however this notion is fraught with danger and ultimately leads to contradictions. One should not simply assume that the electromagnetic fields are a wave-function for the photon. For one thing, they are real and thus contain both positive and negative frequency components, which cannot be reconciled with the requirement for Schroedinger wavefunctions which are complex, positive frequency only. In addition, the electromagnetic fields are observable (e.g. with an oscilloscope) while Schroedinger wavefunctions are not observable, even in principle. Clearly, then, the fields are not wavefunctions, are physical, observable fields, rather than merely what you take the modulus-square of to obtain the probability of finding a photon somewhere. The existence of some "wavefunction of the photon" is not a fully settled issue.http://adsabs.harvard.edu/abs/2005quant.ph..8202B
See also
- Theoretical and experimental justification for the Schrödinger equationTheoretical and experimental justification for the Schrödinger equationThe theoretical and experimental justification for the Schrödinger equation motivates the discovery of the Schrödinger equation, the equation that describes the dynamics of nonrelativistic particles...
- Stern–Gerlach experimentStern–Gerlach experimentImportant in the field of quantum mechanics, the Stern–Gerlach experiment, named after Otto Stern and Walther Gerlach, is a 1922 experiment on the deflection of particles, often used to illustrate basic principles of quantum mechanics...
- Wave-particle duality
- Photon polarizationPhoton polarizationPhoton polarization is the quantum mechanical description of the classical polarized sinusoidal plane electromagnetic wave. Individual photons are completely polarized...
- Photoelectric effectPhotoelectric effectIn the photoelectric effect, electrons are emitted from matter as a consequence of their absorption of energy from electromagnetic radiation of very short wavelength, such as visible or ultraviolet light. Electrons emitted in this manner may be referred to as photoelectrons...

