
Obstacle problem
Encyclopedia
The obstacle problem is a classic motivating example in the mathematical study of variational inequalities and free boundary problem
s. The problem is to find the equilibrium
position of an elastic membrane
whose boundary is held fixed, and which is constrained to lie above a given obstacle. It is deeply related to the study of minimal surfaces and the capacity of a set
in potential theory
as well. Applications include the study of fluid filtration in porous media, constrained heating, elasto-plasticity, optimal control, and financial mathematics.
The mathematical formulation of the problem is to seek minimizers of the Dirichlet energy
functional,
in some domain where the functions
where the functions  represent the vertical displacement of the membrane. In addition to satisfying Dirichlet boundary conditions corresponding to the fixed boundary of the membrane, the functions
represent the vertical displacement of the membrane. In addition to satisfying Dirichlet boundary conditions corresponding to the fixed boundary of the membrane, the functions  are in addition constrained to be greater than some given obstacle function
are in addition constrained to be greater than some given obstacle function 
 . The solution breaks down into a region where the solution is equal to the obstacle function, known as the contact set, and a region where the solution is above the obstacle. The interface between the two regions is the free boundary.
. The solution breaks down into a region where the solution is equal to the obstacle function, known as the contact set, and a region where the solution is above the obstacle. The interface between the two regions is the free boundary.
In general, the solution is continuous and possesses Lipschitz continuous
first derivatives, but that the solution is generally discontinuous in the second derivatives across the free boundary. The free boundary is characterized as a Hölder continuous surface except at certain singular points, which reside on a smooth manifold.
), with the added constraint that the membrane is constrained to lie above some obstacle
 in the interior of the domain as well. In this case, the energy functional to be minimized is the surface area integral, or
in the interior of the domain as well. In this case, the energy functional to be minimized is the surface area integral, or
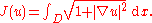
This problem can be linearized in the case of small perturbations by expanding the energy functional in terms of its Taylor series
and taking the first term only, in which case the energy to be minimized is the standard Dirichlet energy
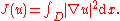
, specifically the question of finding the optimal stopping time for a stochastic process
with payoff function
 .
.
In the simple case where the process is Brownian motion
, and the process is forced to stop upon exiting the domain, the solution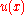 of the obstacle problem can be characterized as the expected value of the payoff, starting the process at
of the obstacle problem can be characterized as the expected value of the payoff, starting the process at  , if the optimal stopping strategy is followed. The stopping criterion is simply that one should stop upon reaching the contact set.
, if the optimal stopping strategy is followed. The stopping criterion is simply that one should stop upon reaching the contact set.
Then consider the set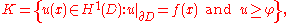
which is a closed
convex
subset
of the Sobolev space
of square integrable functions with square integrable weak first derivatives
, containing precisely those functions with the desired boundary conditions which are also above the obstacle. The solution to the obstacle problem is the function which minimizes the energy integral
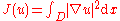
over all functions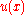 belonging to
belonging to  ; the existence of such a minimizer is assured by considerations of Hilbert space
; the existence of such a minimizer is assured by considerations of Hilbert space
theory.
on Hilbert space
s. Seeking the energy minimizer in the set of suitable functions is equivalent to seeking
of suitable functions is equivalent to seeking
 such that
such that 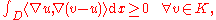
where ⟨ . , . ⟩ : ℝn × ℝn → ℝ is the ordinary scalar product in the finite dimensional real
vector space
ℝn. This is a special case of the more general form for variational inequalities on Hilbert spaces, whose solutions are functions in some closed convex subset
in some closed convex subset  of the overall space, such that
of the overall space, such that
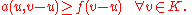
for coercive
, real-valued, bounded
bilinear forms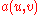 and bounded linear functional
and bounded linear functional
s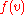 .
.
In fact, an application of the maximum principle
then shows that the solution to the obstacle problem is the least superharmonic function in the set of admissible functions.
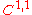 regularity, or bounded
regularity, or bounded
second derivatives, when the obstacle itself has these properties. More precisely, the solution's modulus of continuity
and the modulus of continuity for its derivative
are related to those of the obstacle.
 for
for  are
are 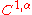 surfaces. The free boundary, which is the boundary of the set where the solution meets the obstacle, is also
surfaces. The free boundary, which is the boundary of the set where the solution meets the obstacle, is also 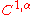 except on a set of singular points, which are themselves either isolated or locally contained on a
except on a set of singular points, which are themselves either isolated or locally contained on a  manifold.
manifold.
s, and their associated energy functionals. It can be generalized to degenerate elliptic operators as well.
The double obstacle problem, where the function is constrained to lie above one obstacle function and below another, is also of interest.
The Signorini problem
is a variant of the obstacle problem, where the energy functional is minimized subject to a constraint which only lives on a surface of one lesser dimension, which includes the boundary obstacle problem, where the constraint operates on the boundary of the domain.
The parabolic
, time-dependent cases of the obstacle problem and its variants are also objects of study.
Free boundary problem
In mathematics, a free boundary problem is a partial differential equation to be solved for both an unknown function u and an unknown domain Ω. The segment Γ of the boundary of Ω which is not known at the outset of the problem is the free boundary....
s. The problem is to find the equilibrium
Mechanical equilibrium
A standard definition of static equilibrium is:This is a strict definition, and often the term "static equilibrium" is used in a more relaxed manner interchangeably with "mechanical equilibrium", as defined next....
position of an elastic membrane
Solid mechanics
Solid mechanics is the branch of mechanics, physics, and mathematics that concerns the behavior of solid matter under external actions . It is part of a broader study known as continuum mechanics. One of the most common practical applications of solid mechanics is the Euler-Bernoulli beam equation...
whose boundary is held fixed, and which is constrained to lie above a given obstacle. It is deeply related to the study of minimal surfaces and the capacity of a set
Capacity of a set
In mathematics, the capacity of a set in Euclidean space is a measure of that set's "size". Unlike, say, Lebesgue measure, which measures a set's volume or physical extent, capacity is a mathematical analogue of a set's ability to hold electrical charge. More precisely, it is the capacitance of...
in potential theory
Potential theory
In mathematics and mathematical physics, potential theory may be defined as the study of harmonic functions.- Definition and comments :The term "potential theory" was coined in 19th-century physics, when it was realized that the fundamental forces of nature could be modeled using potentials which...
as well. Applications include the study of fluid filtration in porous media, constrained heating, elasto-plasticity, optimal control, and financial mathematics.
The mathematical formulation of the problem is to seek minimizers of the Dirichlet energy
Dirichlet energy
In mathematics, the Dirichlet's energy is a numerical measure of how variable a function is. More abstractly, it is a quadratic functional on the Sobolev space...
functional,

in some domain
 where the functions
where the functions  represent the vertical displacement of the membrane. In addition to satisfying Dirichlet boundary conditions corresponding to the fixed boundary of the membrane, the functions
represent the vertical displacement of the membrane. In addition to satisfying Dirichlet boundary conditions corresponding to the fixed boundary of the membrane, the functions  are in addition constrained to be greater than some given obstacle function
are in addition constrained to be greater than some given obstacle function 
 . The solution breaks down into a region where the solution is equal to the obstacle function, known as the contact set, and a region where the solution is above the obstacle. The interface between the two regions is the free boundary.
. The solution breaks down into a region where the solution is equal to the obstacle function, known as the contact set, and a region where the solution is above the obstacle. The interface between the two regions is the free boundary.In general, the solution is continuous and possesses Lipschitz continuous
Lipschitz continuity
In mathematical analysis, Lipschitz continuity, named after Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively, a Lipschitz continuous function is limited in how fast it can change: for every pair of points on the graph of this function, the absolute value of the...
first derivatives, but that the solution is generally discontinuous in the second derivatives across the free boundary. The free boundary is characterized as a Hölder continuous surface except at certain singular points, which reside on a smooth manifold.
Shape of a membrane above an obstacle
The obstacle problem arises when one considers the shape taken by a soap film in a domain whose boundary position is fixed (see Plateau's problemPlateau's problem
In mathematics, Plateau's problem is to show the existence of a minimal surface with a given boundary, a problem raised by Joseph-Louis Lagrange in 1760. However, it is named after Joseph Plateau who was interested in soap films. The problem is considered part of the calculus of variations...
), with the added constraint that the membrane is constrained to lie above some obstacle

 in the interior of the domain as well. In this case, the energy functional to be minimized is the surface area integral, or
in the interior of the domain as well. In this case, the energy functional to be minimized is the surface area integral, or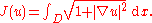
This problem can be linearized in the case of small perturbations by expanding the energy functional in terms of its Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
and taking the first term only, in which case the energy to be minimized is the standard Dirichlet energy
Dirichlet energy
In mathematics, the Dirichlet's energy is a numerical measure of how variable a function is. More abstractly, it is a quadratic functional on the Sobolev space...
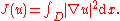
Optimal stopping
The obstacle problem also arises in control theoryControl theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
, specifically the question of finding the optimal stopping time for a stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
with payoff function

 .
.In the simple case where the process is Brownian motion
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
, and the process is forced to stop upon exiting the domain, the solution
 of the obstacle problem can be characterized as the expected value of the payoff, starting the process at
of the obstacle problem can be characterized as the expected value of the payoff, starting the process at  , if the optimal stopping strategy is followed. The stopping criterion is simply that one should stop upon reaching the contact set.
, if the optimal stopping strategy is followed. The stopping criterion is simply that one should stop upon reaching the contact set.Formal statement
Suppose the following data is given:- an openOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
boundedBounded setIn mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
domain ⊂ ℝn with smoothSmooth functionIn mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
⊂ ℝn with smoothSmooth functionIn mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
boundaryBoundary (topology)In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary... - a smooth functionSmooth functionIn mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
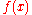 on ∂
on ∂ (the boundaryBoundary (topology)In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
(the boundaryBoundary (topology)In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of )
) - a smooth function

 defined on all of
defined on all of  such that
such that 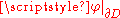 <
<  , i.e. the restriction of
, i.e. the restriction of 
 to the boundary of
to the boundary of  (its traceTrace operatorIn mathematics, the concept of trace operator plays an important role in studying the existence and uniqueness of solutions to boundary value problems, that is, to partial differential equations with prescribed boundary conditions...
(its traceTrace operatorIn mathematics, the concept of trace operator plays an important role in studying the existence and uniqueness of solutions to boundary value problems, that is, to partial differential equations with prescribed boundary conditions...
) is less than .
.
Then consider the set
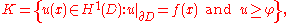
which is a closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
convex
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of the Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
of square integrable functions with square integrable weak first derivatives
Weak derivative
In mathematics, a weak derivative is a generalization of the concept of the derivative of a function for functions not assumed differentiable, but only integrable, i.e. to lie in the Lebesgue space L^1. See distributions for an even more general definition.- Definition :Let u be a function in the...
, containing precisely those functions with the desired boundary conditions which are also above the obstacle. The solution to the obstacle problem is the function which minimizes the energy integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
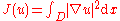
over all functions
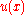 belonging to
belonging to  ; the existence of such a minimizer is assured by considerations of Hilbert space
; the existence of such a minimizer is assured by considerations of Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
theory.
Variational inequality
The obstacle problem can be reformulated as a standard problem in the theory of variational inequalitiesVariational inequality
In mathematics, a variational inequality is an inequality involving a functional, which has to be solved for all the value of a given variable, belonging usually to a convex set...
on Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s. Seeking the energy minimizer in the set
 of suitable functions is equivalent to seeking
of suitable functions is equivalent to seeking such that
such that 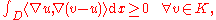
where ⟨ . , . ⟩ : ℝn × ℝn → ℝ is the ordinary scalar product in the finite dimensional real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
ℝn. This is a special case of the more general form for variational inequalities on Hilbert spaces, whose solutions are functions
 in some closed convex subset
in some closed convex subset  of the overall space, such that
of the overall space, such that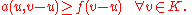
for coercive
Coercive function
In mathematics, a coercive function is a function that "grows rapidly" at the extremes of the space on which it is defined. More precisely, a function f : Rn → Rn is called coercive if...
, real-valued, bounded
Bounded operator
In functional analysis, a branch of mathematics, a bounded linear operator is a linear transformation L between normed vector spaces X and Y for which the ratio of the norm of L to that of v is bounded by the same number, over all non-zero vectors v in X...
bilinear forms
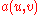 and bounded linear functional
and bounded linear functionalLinear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
s
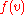 .
.Least superharmonic function
A variational argument shows that, away from the contact set, the solution to the obstacle problem is harmonic. A similar argument which restricts itself to variations that are positive shows that the solution is superharmonic on the contact set. Together, the two arguments imply that the solution is a superharmonic function.In fact, an application of the maximum principle
Maximum principle
In mathematics, the maximum principle is a property of solutions to certain partial differential equations, of the elliptic and parabolic types. Roughly speaking, it says that the maximum of a function in a domain is to be found on the boundary of that domain...
then shows that the solution to the obstacle problem is the least superharmonic function in the set of admissible functions.
Regularity properties
Optimal regularity
The solution to the obstacle problem has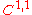 regularity, or bounded
regularity, or boundedBounded function
In mathematics, a function f defined on some set X with real or complex values is called bounded, if the set of its values is bounded. In other words, there exists a real number M...
second derivatives, when the obstacle itself has these properties. More precisely, the solution's modulus of continuity
Modulus of continuity
In mathematical analysis, a modulus of continuity is a function\omega:[0,\infty]\to[0,\infty]used to measure quantitatively the uniform continuity of functions. So, a function f:I\to\R admits \omega as a modulus of continuity if and only if|f-f|\leq\omega,for all x and y in the domain of f...
and the modulus of continuity for its derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
are related to those of the obstacle.
- If the obstacle
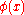 has modulus of continuity
has modulus of continuity 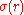 , that is to say that
, that is to say that 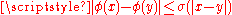 , then the solution
, then the solution 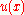 has modulus of continuity given by
has modulus of continuity given by 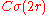 , where the constant depends only on the domain and not the obstacle.
, where the constant depends only on the domain and not the obstacle. - If the obstacle's first derivative has modulus of continuity
 , then the solution's first derivative has modulus of continuity given by
, then the solution's first derivative has modulus of continuity given by  , where the constant again depends only on the domain.
, where the constant again depends only on the domain.
Level surfaces and the free boundary
Subject to a degeneracy condition, level sets of the difference between the solution and the obstacle, for
for  are
are 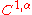 surfaces. The free boundary, which is the boundary of the set where the solution meets the obstacle, is also
surfaces. The free boundary, which is the boundary of the set where the solution meets the obstacle, is also 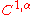 except on a set of singular points, which are themselves either isolated or locally contained on a
except on a set of singular points, which are themselves either isolated or locally contained on a  manifold.
manifold.Generalizations
The theory of the obstacle problem is extended to other divergence form uniformly elliptic operatorElliptic operator
In the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is...
s, and their associated energy functionals. It can be generalized to degenerate elliptic operators as well.
The double obstacle problem, where the function is constrained to lie above one obstacle function and below another, is also of interest.
The Signorini problem
Signorini problem
The Signorini problem is an elastostatics problem in linear elasticity: it consists in finding the elastic equilibrium configuration of an anisotropic non-homogeneous elastic body, resting on a rigid frictionless surface and subject only to its mass forces...
is a variant of the obstacle problem, where the energy functional is minimized subject to a constraint which only lives on a surface of one lesser dimension, which includes the boundary obstacle problem, where the constraint operates on the boundary of the domain.
The parabolic
Parabolic partial differential equation
A parabolic partial differential equation is a type of second-order partial differential equation , describing a wide family of problems in science including heat diffusion, ocean acoustic propagation, in physical or mathematical systems with a time variable, and which behave essentially like heat...
, time-dependent cases of the obstacle problem and its variants are also objects of study.
See also
- Barrier optionBarrier optionIn finance, a barrier option is a financial derivative which either springs into existence upon the occurrence of the event of the price of the underlying asset breaching a barrier or whose existence is extinguished upon the occurrence of the event of the price of the underlying asset breaching a...
- Minimal surfaceMinimal surfaceIn mathematics, a minimal surface is a surface with a mean curvature of zero.These include, but are not limited to, surfaces of minimum area subject to various constraints....
- Variational inequalityVariational inequalityIn mathematics, a variational inequality is an inequality involving a functional, which has to be solved for all the value of a given variable, belonging usually to a convex set...
- Signorini problemSignorini problemThe Signorini problem is an elastostatics problem in linear elasticity: it consists in finding the elastic equilibrium configuration of an anisotropic non-homogeneous elastic body, resting on a rigid frictionless surface and subject only to its mass forces...

