Montel's theorem
Encyclopedia
In complex analysis
, an area of mathematics
, Montel's theorem refers to one of two theorems
about families of holomorphic function
s. These are named after Paul Montel
, and give conditions under which a family of holomorphic functions is normal
.
subset
of the complex number
s is normal
.
This theorem has the following formally stronger corollary. Suppose that
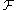is a family of
meromorphic functions on an open set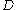
. If 
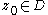is such that
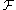is not normal in 
, and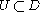 
is a neighborhood of 
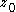, then 
is dense
in the complex plane.
) states that a family of holomorphic functions, all of which omit the same two values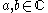
, is normal.
the family
is normal, but does not omit any complex value.
states that a family is normal if and only if the spherical derivatives are locally bounded)
and Cauchy's integral formula
.
This theorem has also been called the Stieltjes–Osgood theorem, after Thomas Joannes Stieltjes
and William Fogg Osgood
.
The Corollary stated above is deduced as follows. Suppose that all the functions in
omit the same neighborhood of the point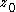 
. By postcomposing with the map 
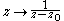we obtain a uniformly bounded family, which is normal by the first version of the theorem.
The second version of Montel's theorem can be deduced from the first by using the fact that there exists a holomorphic universal covering from the unit disk to the twice punctured plane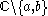
. (Such a covering is given by the elliptic modular function).
However, this version of Montel's theorem can also be proved in a more elementary manner, without the use of covering space theory or the modular function, by using Zalcman's lemma.
For example, the first version of Montel's theorem stated above is the analog of Liouville's theorem
, while the second version corresponds to Picard's theorem.
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, an area of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Montel's theorem refers to one of two theorems
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
about families of holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s. These are named after Paul Montel
Paul Antoine Aristide Montel
Paul Antoine Aristide Montel was a French mathematician. He was born in Nice, France and died in Paris, France. He researched mostly on holomorphic functions in complex analysis....
, and give conditions under which a family of holomorphic functions is normal
Normal family
In mathematics, with special application to complex analysis, a normal family is a pre-compact family of continuous functions. Informally, this means that the functions in the family are not exceedingly numerous or widely spread out; rather, they stick together in a relatively "compact" manner...
.
Uniformly bounded families are normal
The first, and simpler, version of the theorem states that a uniformly bounded family of holomorphic functions defined on an openOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s is normal
Normal family
In mathematics, with special application to complex analysis, a normal family is a pre-compact family of continuous functions. Informally, this means that the functions in the family are not exceedingly numerous or widely spread out; rather, they stick together in a relatively "compact" manner...
.
This theorem has the following formally stronger corollary. Suppose that
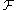is a family ofmeromorphic functions on an open set
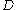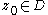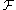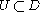. If is such that is not normal in , and is a neighborhood of 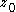, then is densein the complex plane.
Functions omitting two values
The stronger version of Montel's Theorem (occasionally referred to as the Fundamental Normality TestFundamental normality test
In complex analysis, a mathematical discipline, the fundamental normality test gives sufficient conditions to test the normality of a family of analytic functions.-Statement of theorem:...
) states that a family of holomorphic functions, all of which omit the same two values
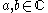, is normal.Necessity
The conditions in the above theorems are sufficient, but not necessary for normality. Indeed,the family
is normal, but does not omit any complex value.Proofs
The first version of Montel's theorem is a direct consequence of Marty's Theorem (whichstates that a family is normal if and only if the spherical derivatives are locally bounded)
and Cauchy's integral formula
Cauchy's integral formula
In mathematics, Cauchy's integral formula, named after Augustin-Louis Cauchy, is a central statement in complex analysis. It expresses the fact that a holomorphic function defined on a disk is completely determined by its values on the boundary of the disk, and it provides integral formulas for all...
.
This theorem has also been called the Stieltjes–Osgood theorem, after Thomas Joannes Stieltjes
Thomas Joannes Stieltjes
Thomas Joannes Stieltjes was a Dutch mathematician. He was born in Zwolle and died in Toulouse, France. He was a pioneer in the field of moment problems and contributed to the study of continued fractions....
and William Fogg Osgood
William Fogg Osgood
William Fogg Osgood was an American mathematician, born in Boston.In 1886, he graduated from Harvard, where, after studying at the universities of Göttingen and Erlangen , he was instructor , assistant professor , and thenceforth professor of mathematics...
.
The Corollary stated above is deduced as follows. Suppose that all the functions in
omit the same neighborhood of the point 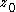. By postcomposing with the map 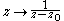we obtain a uniformly bounded family, which is normal by the first version of the theorem.The second version of Montel's theorem can be deduced from the first by using the fact that there exists a holomorphic universal covering from the unit disk to the twice punctured plane
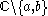. (Such a covering is given by the elliptic modular function).However, this version of Montel's theorem can also be proved in a more elementary manner, without the use of covering space theory or the modular function, by using Zalcman's lemma.
Relationship to theorems for entire functions
A heuristic principle known as Bloch's principle (made precise by a result by Larry Zalcman) states that properties that imply that an entire function is constant correspond to properties that ensure that a family of holomorphic functions is normal.For example, the first version of Montel's theorem stated above is the analog of Liouville's theorem
Liouville's theorem
Liouville's theorem has various meanings, all mathematical results named after Joseph Liouville:*In complex analysis, see Liouville's theorem ; there is also a related theorem on harmonic functions....
, while the second version corresponds to Picard's theorem.