
Normal family
Encyclopedia
In mathematics
, with special application to complex analysis
, a normal family is a pre-compact
family of continuous function
s. Informally, this means that the functions in the family are not exceedingly numerous or widely spread out; rather, they stick together in a relatively "compact" manner. It is of general interest to understand compact sets in function space
s, since these are usually truly infinite-dimensional in nature.
More formally, a family (that is, a set) F of continuous functions f defined on some complete metric space X with values in another complete metric space Y is called normal if every sequence
of functions in F contains a subsequence
which converges uniformly on compact subsets
of X to a continuous function from X to Y.
s. As a consequence of Cauchy's integral theorem
, a sequence of holomorphic functions that converges uniformly on compact sets must converge to a holomorphic function. Thus in complex analysis a normal family F of holomorphic functions in a region X of the complex plane with values in Y = C is such that every sequence in 'F' contains a subsequence which converges uniformly on compact subsets of X to a holomorphic function. Montel's theorem
asserts that every locally bounded family of holomorphic functions is normal.
Another space where this is often used is the space of meromorphic function
s. This is similar to the holomorphic case, but instead of using the standard metric
(distance) for convergence we must use the spherical metric
. That is if d is the spherical metric, then want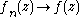
compactly to mean that
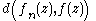
goes to 0 uniformly on compact subsets.
Note that this is a classical definition that, while very often used, is not really consistent with modern naming. In more modern language, one would give a metric on the space of continuous (holomorphic) functions that corresponds to convergence on compact subsets and then you would say "precompact set of functions" in such a metric space instead of saying "normal family of continuous (holomorphic) functions". This added generality however makes it more cumbersome to use since one would need to define the metric mentioned above.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, with special application to complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, a normal family is a pre-compact
Relatively compact subspace
In mathematics, a relatively compact subspace Y of a topological space X is a subset whose closure is compact....
family of continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s. Informally, this means that the functions in the family are not exceedingly numerous or widely spread out; rather, they stick together in a relatively "compact" manner. It is of general interest to understand compact sets in function space
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
s, since these are usually truly infinite-dimensional in nature.
More formally, a family (that is, a set) F of continuous functions f defined on some complete metric space X with values in another complete metric space Y is called normal if every sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of functions in F contains a subsequence
Subsequence
In mathematics, a subsequence is a sequence that can be derived from another sequence by deleting some elements without changing the order of the remaining elements...
which converges uniformly on compact subsets
Compact convergence
In mathematics compact convergence is a type of convergence which generalizes the idea of uniform convergence. It is associated with the compact-open topology.-Definition:...
of X to a continuous function from X to Y.
Complex analysis
This definition is often used in complex analysis for spaces of holomorphic functionHolomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s. As a consequence of Cauchy's integral theorem
Cauchy's integral theorem
In mathematics, the Cauchy integral theorem in complex analysis, named after Augustin-Louis Cauchy, is an important statement about line integrals for holomorphic functions in the complex plane...
, a sequence of holomorphic functions that converges uniformly on compact sets must converge to a holomorphic function. Thus in complex analysis a normal family F of holomorphic functions in a region X of the complex plane with values in Y = C is such that every sequence in 'F' contains a subsequence which converges uniformly on compact subsets of X to a holomorphic function. Montel's theorem
Montel's theorem
In complex analysis, an area of mathematics, Montel's theorem refers to one of two theorems about families of holomorphic functions. These are named after Paul Montel, and give conditions under which a family of holomorphic functions is normal....
asserts that every locally bounded family of holomorphic functions is normal.
Another space where this is often used is the space of meromorphic function
Meromorphic function
In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
s. This is similar to the holomorphic case, but instead of using the standard metric
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
(distance) for convergence we must use the spherical metric
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
. That is if d is the spherical metric, then want
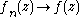
compactly to mean that
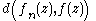
goes to 0 uniformly on compact subsets.
Naming
Paul Montel coined the term "normal family" in 1912.Note that this is a classical definition that, while very often used, is not really consistent with modern naming. In more modern language, one would give a metric on the space of continuous (holomorphic) functions that corresponds to convergence on compact subsets and then you would say "precompact set of functions" in such a metric space instead of saying "normal family of continuous (holomorphic) functions". This added generality however makes it more cumbersome to use since one would need to define the metric mentioned above.
Criteria
- 1'st criterion by MontelMontel's theoremIn complex analysis, an area of mathematics, Montel's theorem refers to one of two theorems about families of holomorphic functions. These are named after Paul Montel, and give conditions under which a family of holomorphic functions is normal....
- 2'nd criterion by Montel
- 3rd criterion by Marty. Marty proved criterion of normality for families of meromorphic functionMeromorphic functionIn complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
s in the case of one complexComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
variable.

