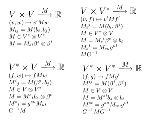
Bilinear operator
Encyclopedia
In mathematics
, a bilinear operator is a function
combining elements of two vector space
s to yield an element of a third vector space that is linear in each of its arguments. Matrix multiplication
is an example.
s over the same base field
F. A bilinear map is a function
such that for any w in W the map
is a linear map from V to X, and for any v in V the map
is a linear map from W to X.
In other words, if we hold the first entry of the bilinear map fixed, while letting the second entry vary, the result is a linear operator, and similarly if we hold the second entry fixed. Note that if we regard the product V × W as a vector space, then B is not a linear transformation
of vector spaces (unless V=0 or W=0) because, for example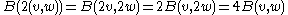 .
.
If V = W and we have B(v,w) = B(w,v) for all v,w in V, then we say that B is symmetric
.
The case where X is F, and we have a bilinear form, is particularly useful (see for example scalar product, inner product and quadratic form
).
The definition works without any changes if instead of vector spaces over a field k, we use modules
over a commutative ring
R. It also can be easily generalized to n-ary functions, where the proper term is multilinear.
For the case of a non-commutative base ring R and a right module MR and a left module RN, we can define a bilinear map B : M × N → T, where T is an abelian group
, such that for any n in N, m → B(m, n) is a group homomorphism, and for any m in M, n → B(m, n) is a group homomorphism too, and which also satisfies
for all m in M, n in N and t in R.
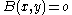
whenever x=o or y=o. (This is seen by writing the null vector
o as 0·o and moving the scalar 0 "outside", in front of B, by linearity.)
The set L(V,W;X) of all bilinear maps is a linear subspace
of the space (viz. vector space
, module
) of all maps from V×W into X.
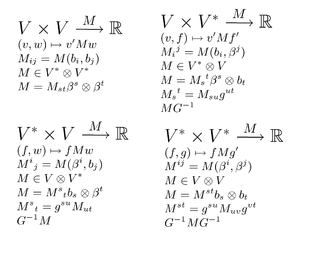 If V,W,X are finite-dimensional, then so is L(V,W;X). For X=F, i.e. bilinear forms, the dimension of this space is dimV×dimW (while the space L(V×W;K) of linear forms is of dimension dimV+dimW). To see this, choose a basis
If V,W,X are finite-dimensional, then so is L(V,W;X). For X=F, i.e. bilinear forms, the dimension of this space is dimV×dimW (while the space L(V×W;K) of linear forms is of dimension dimV+dimW). To see this, choose a basis
for V and W; then each bilinear map can be uniquely represented by the matrix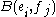 , and vice versa.
, and vice versa.
Now, if X is a space of higher dimension, we obviously have dimL(V,W;X)=dimV×dimW×dimX.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a bilinear operator is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
combining elements of two vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s to yield an element of a third vector space that is linear in each of its arguments. Matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
is an example.
Definition
Let V, W and X be three vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s over the same base field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F. A bilinear map is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
- B : V × W → X
such that for any w in W the map
- v B(v, w)
is a linear map from V to X, and for any v in V the map
- w B(v, w)
is a linear map from W to X.
In other words, if we hold the first entry of the bilinear map fixed, while letting the second entry vary, the result is a linear operator, and similarly if we hold the second entry fixed. Note that if we regard the product V × W as a vector space, then B is not a linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
of vector spaces (unless V=0 or W=0) because, for example
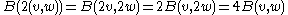 .
.If V = W and we have B(v,w) = B(w,v) for all v,w in V, then we say that B is symmetric
Symmetric function
In algebra and in particular in algebraic combinatorics, the ring of symmetric functions, is a specific limit of the rings of symmetric polynomials in n indeterminates, as n goes to infinity...
.
The case where X is F, and we have a bilinear form, is particularly useful (see for example scalar product, inner product and quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
).
The definition works without any changes if instead of vector spaces over a field k, we use modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
R. It also can be easily generalized to n-ary functions, where the proper term is multilinear.
For the case of a non-commutative base ring R and a right module MR and a left module RN, we can define a bilinear map B : M × N → T, where T is an abelian group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, such that for any n in N, m → B(m, n) is a group homomorphism, and for any m in M, n → B(m, n) is a group homomorphism too, and which also satisfies
- B(mt, n) = B(m, tn)
for all m in M, n in N and t in R.
Properties
A first immediate consequence of the definition is that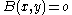
whenever x=o or y=o. (This is seen by writing the null vector
Null vector
Null vector can refer to:* Null vector * A causal structure in Minkowski space...
o as 0·o and moving the scalar 0 "outside", in front of B, by linearity.)
The set L(V,W;X) of all bilinear maps is a linear subspace
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
of the space (viz. vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
, module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
) of all maps from V×W into X.
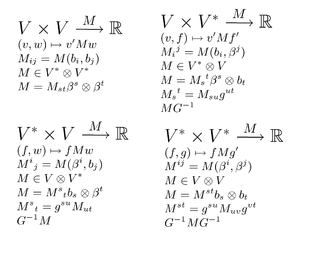
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
for V and W; then each bilinear map can be uniquely represented by the matrix
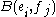 , and vice versa.
, and vice versa.Now, if X is a space of higher dimension, we obviously have dimL(V,W;X)=dimV×dimW×dimX.
Examples
- Matrix multiplicationMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
is a bilinear map M(m,n) × M(n,p) → M(m,p). - If a vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V over the real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s R carries an inner productInner product spaceIn mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
, then the inner product is a bilinear map V × V → R. - In general, for a vector space V over a field F, a bilinear form on V is the same as a bilinear map V × V → F.
- If V is a vector space with dual spaceDual spaceIn mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
V*, then the application operator, b(f, v) = f(v) is a bilinear map from V* × V to the base field. - Let V and W be vector spaces over the same base field F. If f is a member of V* and g a member of W*, then b(v, w) = f(v)g(w) defines a bilinear map V × W → F.
- The cross productCross productIn mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
in R3 is a bilinear map R3 × R3 → R3. - Let B : V × W → X be a bilinear map, and L : U → W be a linear map, then (v, u) → B(v, Lu) is a bilinear map on V × U
- The null map, defined by
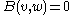 for all (v,w) in V×W is the only map from V×W to X which is bilinear and linear at the same time. Indeed, if (v,w)∈V×W, then if B is linear,
for all (v,w) in V×W is the only map from V×W to X which is bilinear and linear at the same time. Indeed, if (v,w)∈V×W, then if B is linear, 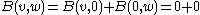 if B is bilinear.
if B is bilinear.
See also
- Tensor productTensor productIn mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
- Sesquilinear formSesquilinear formIn mathematics, a sesquilinear form on a complex vector space V is a map V × V → C that is linear in one argument and antilinear in the other. The name originates from the numerical prefix sesqui- meaning "one and a half"...
- Bilinear filteringBilinear filteringBilinear filtering is a texture filtering method used to smooth textures when displayed larger or smaller than they actually are.Most of the time, when drawing a textured shape on the screen, the texture is not displayed exactly as it is stored, without any distortion...
- Multilinear map

