
Janko group J1
Encyclopedia
In mathematics
, the smallest Janko group
, J1, is a simple sporadic group
of order 175560. It was originally described by Zvonimir Janko
(1965) and was the first sporadic group to be found since the discovery of the Mathieu group
s in the 19th century. Its discovery launched the modern theory of sporadic group
s.
with abelian 2-Sylow subgroups and with an involution whose centralizer is isomorphic to the direct product
of the group of order two and the alternating group A5 of order 60, which is to say, the rotational icosahedral group
. That was Janko's original conception of the group.
In fact Janko and Thompson
were investigating groups similar to the Ree groups 2G2(32n+1), and showed that if a simple group G has abelian Sylow 2-subgroups and a centralizer of an involution of the form Z/2Z×PSL2(q) for q a prime power at least 3, then either
q is a power of 3 and G has the same order as a Ree group (it was later shown that G must be a Ree group in this case) or q is 4 or 5. Note that PSL2(4)=PSL2(5)=A5. This last exceptional case led to the Janko group J1.
J1 has no outer automorphisms
and its Schur multiplier
is trivial.
J1 is the smallest of the 6 sporadic simple groups called the pariahs
, because they are not found within the Monster group
. J1 is contained in the O'Nan group
as the subgroup of elements fixed by an outer automorphism of order 2.
matrices in the field of eleven elements
, with generators given by
and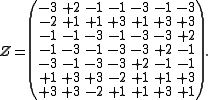
Y has order 7 and Z has order 5. Janko (1966) credited W. A. Coppel for recognizing this representation as an embedding into Dickson's
simple groupG2(11)
(which has a 7 dimensional representation over the field with 11 elements).
There is also a pair of generators a, b such that
J1 is thus a Hurwitz group, a finite homomorphic image of the (2,3,7) triangle group
.
Here is a complete list of the maximal subgroups.
The notation A.B means a group with a normal subgroup A with quotient B, and
D2n is the dihedral group of order 2n.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the smallest Janko group
Janko group
In mathematics, a Janko group is one of the four sporadic simple groups named for Zvonimir Janko. Janko constructed the first Janko group J1 in 1965. At the same time, Janko also predicted the existence of J2 and J3. In 1976, he suggested the existence of J4...
, J1, is a simple sporadic group
Sporadic group
In the mathematical field of group theory, a sporadic group is one of the 26 exceptional groups in the classification of finite simple groups. A simple group is a group G that does not have any normal subgroups except for the subgroup consisting only of the identity element, and G itself...
of order 175560. It was originally described by Zvonimir Janko
Zvonimir Janko
Zvonimir Janko is a Croatian mathematician who is the eponym of the Janko groups, sporadic simple groups in group theory.Janko was born in Bjelovar, Croatia. He studied at the University of Zagreb where he received Ph.D. in 1960. He then taught physics at a high school in Široki Brijeg in Bosnia...
(1965) and was the first sporadic group to be found since the discovery of the Mathieu group
Mathieu group
In the mathematical field of group theory, the Mathieu groups, named after the French mathematician Émile Léonard Mathieu, are five finite simple groups he discovered and reported in papers in 1861 and 1873; these were the first sporadic simple groups discovered...
s in the 19th century. Its discovery launched the modern theory of sporadic group
Sporadic group
In the mathematical field of group theory, a sporadic group is one of the 26 exceptional groups in the classification of finite simple groups. A simple group is a group G that does not have any normal subgroups except for the subgroup consisting only of the identity element, and G itself...
s.
Properties
J1 can be characterized abstractly as the unique simple groupSimple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
with abelian 2-Sylow subgroups and with an involution whose centralizer is isomorphic to the direct product
Direct product of groups
In the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
of the group of order two and the alternating group A5 of order 60, which is to say, the rotational icosahedral group
Icosahedral symmetry
A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...
. That was Janko's original conception of the group.
In fact Janko and Thompson
John G. Thompson
John Griggs Thompson is a mathematician at the University of Florida noted for his work in the field of finite groups. He was awarded the Fields Medal in 1970, the Wolf Prize in 1992 and the 2008 Abel Prize....
were investigating groups similar to the Ree groups 2G2(32n+1), and showed that if a simple group G has abelian Sylow 2-subgroups and a centralizer of an involution of the form Z/2Z×PSL2(q) for q a prime power at least 3, then either
q is a power of 3 and G has the same order as a Ree group (it was later shown that G must be a Ree group in this case) or q is 4 or 5. Note that PSL2(4)=PSL2(5)=A5. This last exceptional case led to the Janko group J1.
J1 has no outer automorphisms
Outer automorphism group
In mathematics, the outer automorphism group of a group Gis the quotient Aut / Inn, where Aut is the automorphism group of G and Inn is the subgroup consisting of inner automorphisms. The outer automorphism group is usually denoted Out...
and its Schur multiplier
Schur multiplier
In mathematical group theory, the Schur multiplier or Schur multiplicator is the second homology group H_2 of a group G.It was introduced by in his work on projective representations.-Examples and properties:...
is trivial.
J1 is the smallest of the 6 sporadic simple groups called the pariahs
Pariah group
In mathematical group theory, the term pariah was introduced by to refer to the six sporadic simple groups that are not subquotients of the monster simple group.These groups are:*Three of the Janko groups: J1, J3, and J4.*The Lyons group...
, because they are not found within the Monster group
Monster group
In the mathematical field of group theory, the Monster group M or F1 is a group of finite order:...
. J1 is contained in the O'Nan group
O'Nan group
In the mathematical field of group theory, the O'Nan group O'N is a sporadic simple group of orderThe Schur multiplier has order 3, and its outer automorphism group has order 2...
as the subgroup of elements fixed by an outer automorphism of order 2.
Construction
Janko found a modular representation in terms of 7 × 7 orthogonalOrthogonality
Orthogonality occurs when two things can vary independently, they are uncorrelated, or they are perpendicular.-Mathematics:In mathematics, two vectors are orthogonal if they are perpendicular, i.e., they form a right angle...
matrices in the field of eleven elements
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
, with generators given by

and
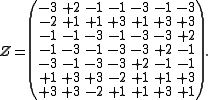
Y has order 7 and Z has order 5. Janko (1966) credited W. A. Coppel for recognizing this representation as an embedding into Dickson's
Leonard Eugene Dickson
Leonard Eugene Dickson was an American mathematician. He was one of the first American researchers in abstract algebra, in particular the theory of finite fields and classical groups, and is also remembered for a three-volume history of number theory.-Life:Dickson considered himself a Texan by...
simple groupG2(11)
Group of Lie type
In mathematics, a group of Lie type G is a group of rational points of a reductive linear algebraic group G with values in the field k. Finite groups of Lie type form the bulk of nonabelian finite simple groups...
(which has a 7 dimensional representation over the field with 11 elements).
There is also a pair of generators a, b such that
- a2=b3=(ab)7=(abab−1)19=1
J1 is thus a Hurwitz group, a finite homomorphic image of the (2,3,7) triangle group
(2,3,7) triangle group
In the theory of Riemann surfaces and hyperbolic geometry, the triangle group is particularly important. This importance stems from its connection to Hurwitz surfaces, namely Riemann surfaces of genus g with the largest possible order, 84, of its automorphism group.A note on terminology – the "...
.
Maximal subgroups
Janko (1966) enumerated all 7 conjugacy classes of maximal subgroups (see also the Atlas webpages cited below). Maximal simple subgroups of order 660 afford J1 a permutation representation of degree 266. He found that there are 2 conjugacy classes of subgroups isomorphic to the alternating group A5, both found in the simple subgroups of order 660. J1 has non-abelian simple proper subgroups of only 2 isomorphism types.Here is a complete list of the maximal subgroups.
| Structure | Order | Index | Description |
|---|---|---|---|
| PSL2(11) | 660 | 266 | Fixes point in smallest permutation representation |
| 23.7.3 | 168 | 1045 | Normalizer of Sylow 2-subgroup |
| 2×A5 | 120 | 1463 | Centralizer of involution |
| 19.6 | 114 | 1540 | Normalizer of Sylow 19-subgroup |
| 11.10 | 110 | 1596 | Normalizer of Sylow 11-subgroup |
| D6×D10 | 60 | 2926 | Normalizer of Sylow 3-subgroup and Sylow 5-subgroup |
| 7.6 | 42 | 4180 | Normalizer of Sylow 7-subgroup |
The notation A.B means a group with a normal subgroup A with quotient B, and
D2n is the dihedral group of order 2n.
Number of elements of each order
The greatest order of any element of the group is 19. The conjugacy class orders and sizes are found in the ATLAS.| Order | No. elements | Conjugacy |
|---|---|---|
| 1 = 1 | 1 = 1 | 1 class |
| 2 = 2 | 1463 = 7 · 11 · 19 | 1 class |
| 3 = 3 | 5852 = 22 · 7 · 11 · 19 | 1 class |
| 5 = 5 | 11704 = 23 · 7 · 11 · 19 | 2 classes, power equivalent |
| 6 = 2 · 3 | 29260 = 22 · 5 · 7 · 11 · 19 | 1 class |
| 7 = 7 | 25080 = 23 · 3 · 5 · 11 · 19 | 1 class |
| 10 = 2 · 5 | 35112 = 23 · 3 · 7 · 11 · 19 | 2 classes, power equivalent |
| 11 = 11 | 15960 = 23 · 3 · 5 · 7 · 19 | 1 class |
| 15 = 3 · 5 | 23408 = 24 · 7 · 11 · 19 | 2 classes, power equivalent |
| 19 = 19 | 27720 = 23 · 32 · 5 · 7 · 11 | 3 classes, power equivalent |

