Monster group
Encyclopedia
In the mathematical field of group theory
, the Monster group M or F1 (also known as the Fischer-Griess Monster, or the Friendly Giant) is a group
of finite order
:
It is a simple group
, meaning it does not have any normal subgroup
s except for the subgroup consisting only of the identity element, and M itself.
The finite simple groups have been completely classified (the classification of finite simple groups
). The list of finite simple groups consists of 18 countably infinite families, plus 26 sporadic groups that do not follow such a systematic pattern. The Monster group is the largest of these sporadic groups and contains all but six of the other sporadic groups as subquotient
s. Robert Griess has called these six exceptions pariahs
, and refers to the others as the happy family.
Probably the best definition is that the Monster is the smallest simple group containing both the Conway groups and the Fischer groups as subquotients.
(unpublished) and in about 1973 as a simple group containing a double cover of Fischer's baby monster group
as a centralizer of an involution. Within a few months the order of M was found by Griess using the Thompson order formula
, and Fischer, Conway, Norton and Thompson discovered other groups as subquotients, including many of the known sporadic groups, and two new ones: the Thompson group
and the Harada-Norton group
. constructed M as the automorphism group of the Griess algebra
, a 196884-dimensional commutative nonassociative algebra. John Conway
and Jacques Tits
subsequently simplified this construction.
Griess's construction showed that the Monster existed. John G. Thompson
showed that its uniqueness (as a simple group of the given order) would follow from the existence of a 196883-dimensional faithful representation. A proof of the existence of such a representation was announced in 1982 by Simon P. Norton
, though he has never published the details. The first published proof of the uniqueness of the Monster was completed by .
The character table
of the Monster, a 194-by-194 array, was calculated in 1979 by Fischer and Livingstone using computer programs written by Thorne. The calculation was based on the assumption that the minimal degree of a faithful complex representation is 196883, which is the product of the 3 largest prime divisors of the order of M.
conjecture by Conway and Norton, which relates discrete and non-discrete mathematics and was finally proved by Richard Borcherds in 1992.
In this setting, the Monster group is visible as the automorphism group of the Monster module, a vertex operator algebra
, an infinite dimensional algebra containing the Griess algebra, and acts on the Monster Lie algebra
, a generalized Kac-Moody algebra.
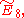specifically between the nodes of the diagram and certain conjugacy classes in the monster, known as McKay's E8 observation. This is then extended to a relation between the extended diagrams 
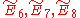and the groups 3.Fi24', 2.B, and M, where these are (3/2/1-fold central extensions) of the Fischer group
, baby monster group
, and monster. These are the sporadic group
s associated with centralizers of elements of type 1A, 2A, and 3A in the monster, and the order of the extension corresponds to the symmetries of the diagram. See ADE classification: trinities for further connections (of McKay correspondence type), including (for the monster) with the rather small simple group PSL(2,11) and with the 120 tritangent planes of a canonic sextic curve of genus 4.
has found explicitly (with the aid of a computer) two 196882 by 196882 matrices (with elements in the field
of order 2) which together generate the Monster group; note that this is dimension 1 lower than the 196883-dimensional representation in characteristic 0. However, performing calculations with these matrices is prohibitively expensive in terms of time and storage space. Wilson with collaborators has found a method of performing calculations with the Monster that is considerably faster.
Let V be a 196882 dimensional vector space over the field with 2 elements. A large subgroup H (preferably a maximal subgroup) of the Monster is selected in which it is easy to perform calculations. The subgroup H chosen is 31+12.2.Suz.2, where Suz is the Suzuki group
. Elements of the Monster are stored as words in the elements of H and an extra generator T. It is reasonably quick to calculate the action of one of these words on a vector in V. Using this action, it is possible to perform calculations (such as the order of an element of the Monster). Wilson has exhibited vectors u and v whose joint stabilizer is the trivial group. Thus (for example) one can calculate the order of an element g of the Monster by finding the smallest i > 0 such that giu = u and giv = v.
This and similar constructions (in different characteristics
) have been used to prove some interesting properties of the Monster (for example, to find some of its non-local maximal subgroups).
The Monster has at least 43 conjugacy classes of maximal subgroups. Non-abelian simple groups of some 60 isomorphism types are found as subgroups or as quotients of subgroups. The largest alternating group represented is A12.
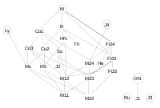
The Monster contains many but not all of the 26 sporadic groups as subgroups. This diagram, based on one in the book Symmetry and the Monster by Mark Ronan
, shows how they fit together. The lines signify inclusion, as a subquotient, of the lower group by the upper one. The circled symbols denote groups not involved in larger sporadic groups. For the sake of clarity redundant inclusions are not shown.
over the rational number
s , and as a Hurwitz group .
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, the Monster group M or F1 (also known as the Fischer-Griess Monster, or the Friendly Giant) is a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of finite order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
:
| 246 · 320 · 59 · 76 · 112 · 133 · 17 · 19 · 23 · 29 · 31 · 41 · 47 · 59 · 71 | |
| = | 808,017,424,794,512,875,886,459,904,961,710,757,005,754,368,000,000,000 |
| ≈ | 8 · 1053 |
It is a simple group
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
, meaning it does not have any normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
s except for the subgroup consisting only of the identity element, and M itself.
The finite simple groups have been completely classified (the classification of finite simple groups
Classification of finite simple groups
In mathematics, the classification of the finite simple groups is a theorem stating that every finite simple group belongs to one of four categories described below. These groups can be seen as the basic building blocks of all finite groups, in much the same way as the prime numbers are the basic...
). The list of finite simple groups consists of 18 countably infinite families, plus 26 sporadic groups that do not follow such a systematic pattern. The Monster group is the largest of these sporadic groups and contains all but six of the other sporadic groups as subquotient
Section (group theory)
In group theory a section of a group G is a group that is, or is isomorphic to, a quotient group of a subgroup of G.- Examples :Of the 26 sporadic groups, 20 are sections of the monster group, and are referred to as the "Happy Family"....
s. Robert Griess has called these six exceptions pariahs
Pariah group
In mathematical group theory, the term pariah was introduced by to refer to the six sporadic simple groups that are not subquotients of the monster simple group.These groups are:*Three of the Janko groups: J1, J3, and J4.*The Lyons group...
, and refers to the others as the happy family.
Probably the best definition is that the Monster is the smallest simple group containing both the Conway groups and the Fischer groups as subquotients.
Existence and uniqueness
The Monster was predicted by Bernd FischerBernd Fischer
Bernd Fischer may refer to:* Bernd Fischer , German mathematician.* Bernd Jürgen Fischer, historian and professor of history at Indiana University-Purdue University Fort Wayne....
(unpublished) and in about 1973 as a simple group containing a double cover of Fischer's baby monster group
Baby Monster group
In the mathematical field of group theory, the Baby Monster group B is a group of orderThe Baby Monster group is one of the sporadic groups, and has the second highest order of these, with the highest order being that of the Monster group...
as a centralizer of an involution. Within a few months the order of M was found by Griess using the Thompson order formula
Thompson order formula
In mathematical finite group theory, the Thompson order formula, introduced by John Griggs Thompson, gives a formula for the order of a finite group in terms of the centralizers of involutions.-Statement:...
, and Fischer, Conway, Norton and Thompson discovered other groups as subquotients, including many of the known sporadic groups, and two new ones: the Thompson group
Thompson group (finite)
In the mathematical field of group theory, the Thompson group Th, found by and constructed by , is a sporadic simple group of orderThe centralizer of an element of order 3 of type 3C in the Monster group is a product of the Thompson group and a group of order 3, as a result of which the Thompson...
and the Harada-Norton group
Harada-Norton group
In the mathematical field of group theory, the Harada–Norton group HN is a sporadic simple group of orderThe Harada–Norton group has an involution whose centralizer is of the form 2.HS.2, where HS is the Higman-Sims group .The prime 5 plays a special role in the group...
. constructed M as the automorphism group of the Griess algebra
Griess algebra
In mathematics, the Griess algebra is a commutative non-associative algebra on a real vector space of dimension 196884 that has the Monster group M as its automorphism group. It is named after mathematician R. L. Griess, who constructed it in 1980 and subsequently used it in 1982 to construct M...
, a 196884-dimensional commutative nonassociative algebra. John Conway
John Horton Conway
John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
and Jacques Tits
Jacques Tits
Jacques Tits is a Belgian and French mathematician who works on group theory and geometry and who introduced Tits buildings, the Tits alternative, and the Tits group.- Career :Tits received his doctorate in mathematics at the age of 20...
subsequently simplified this construction.
Griess's construction showed that the Monster existed. John G. Thompson
John G. Thompson
John Griggs Thompson is a mathematician at the University of Florida noted for his work in the field of finite groups. He was awarded the Fields Medal in 1970, the Wolf Prize in 1992 and the 2008 Abel Prize....
showed that its uniqueness (as a simple group of the given order) would follow from the existence of a 196883-dimensional faithful representation. A proof of the existence of such a representation was announced in 1982 by Simon P. Norton
Simon P. Norton
Simon Phillips Norton is a mathematician in Cambridge, England, who works on finite simple groups. He constructed the Harada–Norton group, and in 1979 together with John Conway proved there is a connection between the Monster group and the j-function in number theory. They dubbed this monstrous...
, though he has never published the details. The first published proof of the uniqueness of the Monster was completed by .
The character table
Character theory
In mathematics, more specifically in group theory, the character of a group representation is a function on the group which associates to each group element the trace of the corresponding matrix....
of the Monster, a 194-by-194 array, was calculated in 1979 by Fischer and Livingstone using computer programs written by Thorne. The calculation was based on the assumption that the minimal degree of a faithful complex representation is 196883, which is the product of the 3 largest prime divisors of the order of M.
Moonshine
The Monster group is one of two principal constituents in the Monstrous moonshineMonstrous moonshine
In mathematics, monstrous moonshine, or moonshine theory, is a term devised by John Horton Conway and Simon P. Norton in 1979, used to describe the connection between the monster group M and modular functions .- History :Specifically, Conway and Norton, following an initial observationby John...
conjecture by Conway and Norton, which relates discrete and non-discrete mathematics and was finally proved by Richard Borcherds in 1992.
In this setting, the Monster group is visible as the automorphism group of the Monster module, a vertex operator algebra
Vertex operator algebra
In mathematics, a vertex operator algebra is an algebraic structure that plays an important role in conformal field theory and related areas of physics...
, an infinite dimensional algebra containing the Griess algebra, and acts on the Monster Lie algebra
Monster Lie algebra
In mathematics, the monster Lie algebra is an infinitedimensional generalized Kac–Moody algebra acted on by the monster group, which was used to prove the monstrous moonshine conjectures.- Structure :...
, a generalized Kac-Moody algebra.
McKay's E8 observation
There are also connections between the monster and the extended Dynkin diagrams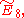 specifically between the nodes of the diagram and certain conjugacy classes in the monster, known as McKay's E8 observation. This is then extended to a relation between the extended diagrams 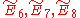and the groups 3.Fi24', 2.B, and M, where these are (3/2/1-fold central extensions) of the Fischer groupFischer group
In mathematics, the Fischer groups are the three sporadic simple groups Fi22, Fi23,Fi24' introduced by .- 3-transposition groups :...
, baby monster group
Baby Monster group
In the mathematical field of group theory, the Baby Monster group B is a group of orderThe Baby Monster group is one of the sporadic groups, and has the second highest order of these, with the highest order being that of the Monster group...
, and monster. These are the sporadic group
Sporadic group
In the mathematical field of group theory, a sporadic group is one of the 26 exceptional groups in the classification of finite simple groups. A simple group is a group G that does not have any normal subgroups except for the subgroup consisting only of the identity element, and G itself...
s associated with centralizers of elements of type 1A, 2A, and 3A in the monster, and the order of the extension corresponds to the symmetries of the diagram. See ADE classification: trinities for further connections (of McKay correspondence type), including (for the monster) with the rather small simple group PSL(2,11) and with the 120 tritangent planes of a canonic sextic curve of genus 4.
A computer construction
Robert A. WilsonRobert Arnott Wilson
Robert Arnott Wilson is a mathematician in London, England, who is best known for his work on classifying the maximal subgroups of finite simple groups and for the work in the Monster group.-Books:...
has found explicitly (with the aid of a computer) two 196882 by 196882 matrices (with elements in the field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
of order 2) which together generate the Monster group; note that this is dimension 1 lower than the 196883-dimensional representation in characteristic 0. However, performing calculations with these matrices is prohibitively expensive in terms of time and storage space. Wilson with collaborators has found a method of performing calculations with the Monster that is considerably faster.
Let V be a 196882 dimensional vector space over the field with 2 elements. A large subgroup H (preferably a maximal subgroup) of the Monster is selected in which it is easy to perform calculations. The subgroup H chosen is 31+12.2.Suz.2, where Suz is the Suzuki group
Suzuki sporadic group
In mathematical group theory, the Suzuki group Suz or Sz is a sporadic simple group of order 213 · 37 · 52· 7 · 11 · 13 = 448345497600 discovered by . It is not related to the Suzuki groups of Lie type....
. Elements of the Monster are stored as words in the elements of H and an extra generator T. It is reasonably quick to calculate the action of one of these words on a vector in V. Using this action, it is possible to perform calculations (such as the order of an element of the Monster). Wilson has exhibited vectors u and v whose joint stabilizer is the trivial group. Thus (for example) one can calculate the order of an element g of the Monster by finding the smallest i > 0 such that giu = u and giv = v.
This and similar constructions (in different characteristics
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
) have been used to prove some interesting properties of the Monster (for example, to find some of its non-local maximal subgroups).
Subgroup structure
The Monster contains many but not all of the 26 sporadic groups as subgroups. This diagram, based on one in the book Symmetry and the Monster by Mark Ronan
Mark Ronan
Mark Andrew Ronan is Emeritus Professor of Mathematics at the University of Illinois at Chicago and Honorary Professor of Mathematics at University College London...
, shows how they fit together. The lines signify inclusion, as a subquotient, of the lower group by the upper one. The circled symbols denote groups not involved in larger sporadic groups. For the sake of clarity redundant inclusions are not shown.
Occurrence
The monster can be realized as a Galois groupGalois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
over the rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s , and as a Hurwitz group .