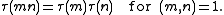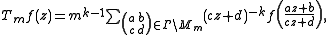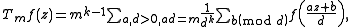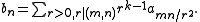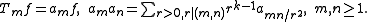In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, in particular in the theory of modular form

Modular form

In mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...

s, a Hecke operator, studied by , is a certain kind of "averaging" operator that plays a significant role in the structure of vector space

Vector space

A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...

s of modular forms and more general automorphic representations.

History

used Hecke operators on modular forms in a paper on the special cusp form

Cusp form

In number theory, a branch of mathematics, a cusp form is a particular kind of modular form, distinguished in the case of modular forms for the modular group by the vanishing in the Fourier series expansion \Sigma a_n q^n...

 of Ramanujan, ahead of the general theory given by . Mordell proved that the Ramanujan tau function, expressing the coefficients of the Ramanujan form,

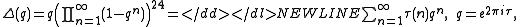
is a multiplicative function

Multiplicative function

In number theory, a multiplicative function is an arithmetic function f of the positive integer n with the property that f = 1 and whenevera and b are coprime, then...

:

The idea goes back to earlier work of Hurwitz

Hurwitz

Hurwitz is a surname and may refer to:*Aaron Hurwitz, musician, see Live on Breeze Hill*Adolf Hurwitz , German mathematician**Hurwitz polynomial**Hurwitz matrix**Hurwitz quaternion**Hurwitz's automorphisms theorem**Hurwitz zeta function...

, who treated algebraic correspondence

Correspondence (mathematics)

In mathematics and mathematical economics, correspondence is a term with several related but not identical meanings.* In general mathematics, correspondence is an alternative term for a relation between two sets...

s between modular curve

Modular curve

In number theory and algebraic geometry, a modular curve Y is a Riemann surface, or the corresponding algebraic curve, constructed as a quotient of the complex upper half-plane H by the action of a congruence subgroup Γ of the modular group of integral 2×2 matrices SL...

s which realise some individual Hecke operators.

Mathematical description

Hecke operators can be realised in a number of contexts. The simplest meaning is combinatorial, namely as taking for a given integer n some function f(Λ) defined on the lattice

Lattice (group)

In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...

s of fixed rank to


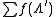
with the sum taken over all the Λ′ that are subgroup

Subgroup

In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...

s of Λ of index n. For example, with n=2 and two dimensions, there are three such Λ′. Modular form

Modular form

In mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...

s are particular kinds of functions of a lattice, subject to conditions making them analytic function

Analytic function

In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...

s and homogeneous

Homogeneous function

In mathematics, a homogeneous function is a function with multiplicative scaling behaviour: if the argument is multiplied by a factor, then the result is multiplied by some power of this factor. More precisely, if is a function between two vector spaces over a field F, and k is an integer, then...

 with respect to homotheties, as well as moderate growth at infinity; these conditions are preserved by the summation, and so Hecke operators preserve the space of modular forms of a given weight.

Another way to express Hecke operators is by means of double coset

Double coset

In mathematics, an double coset in G, where G is a group and H and K are subgroups of G, is an equivalence class for the equivalence relation defined on G by...

s in the modular group

Modular group

In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...

. In the contemporary adelic approach, this translates to double cosets with respect to some compact subgroups.

Explicit formula

Let M_m be the set of 2×2 integral matrices with determinant

Determinant

In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...

 m and Γ = M₁ be the full modular group

Modular group

In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...

 SL(2, Z). Given a modular form f(z) of weight k, the mth Hecke operator acts by the formula

where z is in the upper half-plane and the normalization constant m^k−1 assures that the image of a form with integer Fourier coefficients has integer Fourier coefficients. This can be rewritten in the form

which leads to the formula for the Fourier coefficients of T_mf(z) = ∑ b_nqⁿ in terms of the Fourier coefficients of f(z) = ∑ a_nqⁿ:

One can see from this explicit formula that Hecke operators with different indices commute and that if a₀ = 0 then b₀ = 0, so the subspace S_k of cusp forms of weight k is preserved by the Hecke operators. If a (non-zero) cusp form f is a simultaneous eigenform

Eigenform

An eigenform is a modular form which is an eigenvector for all Hecke operators Tm, m = 1, 2, 3, …....

 of all Hecke operators T_m with eigenvalues λ_m then a_m = λ_ma₁ and a₁ ≠ 0. Hecke eigenforms are normalized so that a₁ = 1, then

Thus for normalized cuspidal Hecke eigenforms of integer weight, their Fourier coefficients coincide with their Hecke eigenvalues.

Hecke algebras

Algebras of Hecke operators are called Hecke algebras, and are commutative ring

Commutative ring

In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....

s. Other, related, mathematical rings are called Hecke algebras, although the link to Hecke operators is not entirely obvious. These algebras include certain quotients of the group algebra

Group algebra

In mathematics, the group algebra is any of various constructions to assign to a locally compact group an operator algebra , such that representations of the algebra are related to representations of the group...

s of braid group

Braid group

In mathematics, the braid group on n strands, denoted by Bn, is a group which has an intuitive geometrical representation, and in a sense generalizes the symmetric group Sn. Here, n is a natural number; if n > 1, then Bn is an infinite group...

s. The presence of this commutative operator algebra plays a significant role in the harmonic analysis

Harmonic analysis

Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...

 of modular forms and generalisations. In the classical elliptic modular form theory, the Hecke operators T_n with n coprime to the level acting on the space of cusp forms of a given weight are self-adjoint

Self-adjoint operator

In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...

 with respect to the Petersson inner product. Therefore, the spectral theorem

Spectral theorem

In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...

 implies that there is a basis of modular forms that are eigenfunction

Eigenfunction

In mathematics, an eigenfunction of a linear operator, A, defined on some function space is any non-zero function f in that space that returns from the operator exactly as is, except for a multiplicative scaling factor. More precisely, one has...

s for these Hecke operators. Each of these basic forms possesses an Euler product

Euler product

In number theory, an Euler product is an expansion of a Dirichlet series into an infinite product indexed by prime numbers. The name arose from the case of the Riemann zeta-function, where such a product representation was proved by Leonhard Euler.-Definition:...

. More precisely, its Mellin transform

Mellin transform

In mathematics, the Mellin transform is an integral transform that may be regarded as the multiplicative version of the two-sided Laplace transform...

 is Dirichlet series that has Euler product

Euler product

In number theory, an Euler product is an expansion of a Dirichlet series into an infinite product indexed by prime numbers. The name arose from the case of the Riemann zeta-function, where such a product representation was proved by Leonhard Euler.-Definition:...

s with the local factor for each prime p is the inverse of the Hecke polynomial, a quadratic polynomial in p^−s. In the case treated by Mordell, the space of cusp forms of weight 12 with respect to the full modular group is one-dimensional. It follows that the Ramanujan form has an Euler product and establishes the multiplicativity of τ(n).

The source of this article is wikipedia, the free encyclopedia.  The text of this article is licensed under the GFDL.