Frequency spectrum
Encyclopedia
The frequency spectrum of a time-domain signal is a representation of that signal in the frequency domain
. The frequency spectrum can be generated via a Fourier transform
of the signal, and the resulting values are usually presented as amplitude
and phase
, both plotted versus frequency
.
Any signal that can be represented as an amplitude that varies with time has a corresponding frequency spectrum. This includes familiar concepts such as visible light (color
), musical notes, radio/TV channels
, and even the regular rotation of the earth. When these physical phenomena are represented in the form of a frequency spectrum, certain physical descriptions of their internal processes become much simpler. Often, the frequency spectrum clearly shows harmonics, visible as distinct spikes or lines, that provide insight into the mechanisms that generate the entire signal.
Similarly, a source of sound can have many different frequencies mixed together. A musical tone's
timbre
is characterized by its harmonic
spectrum
. Sound in our environment that we refer to as noise includes many different frequencies. When a sound signal contains a mixture of all audible frequencies, distributed equally over the audio spectrum, it is called white noise
.
or decode the information from that broadcaster. If we made a graph of the strength of each channel vs. the frequency of the tuner, it would be the frequency spectrum of the antenna signal.
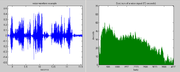
Spectrum analysis is the technical process of decomposing a complex signal into simpler parts. As described above, many physical processes are best described as a sum of many individual frequency components. Any process that quantifies the various amounts (e.g. amplitudes, powers, intensities, or phases), versus frequency can be called spectrum analysis.
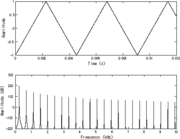
Spectrum analysis can be performed on the entire signal. Alternatively, a signal can be broken into short segments (sometimes called frames), and spectrum analysis may be applied to these individual segments. Periodic function
s (such as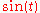
) are particularly well-suited for this sub-division. General mathematical techniques for analyzing non-periodic functions fall into the category of Fourier analysis.
The Fourier transform
of a function produces a frequency spectrum which contains all of the information about the original signal, but in a different form. This means that the original function can be completely reconstructed (synthesized) by an inverse Fourier transform. For perfect reconstruction, the spectrum analyzer must preserve both the amplitude and phase
of each frequency component. These two pieces of information can be represented as a 2-dimensional vector, as a complex number, or as magnitude (amplitude) and phase in polar coordinates. A common technique in signal processing is to consider the squared amplitude, or power
; in this case the resulting plot is referred to as a power spectrum.
In practice, nearly all software and electronic devices that generate frequency spectra apply a fast Fourier transform
(FFT), which is a specific mathematical approximation to the full integral solution. Formally stated, the FFT is a method for computing the discrete Fourier transform
of a sampled signal
.
Because of reversibility, the Fourier transform is called a representation of the function, in terms of frequency instead of time; thus, it is a frequency domain
representation. Linear operations that could be performed in the time domain have counterparts that can often be performed more easily in the frequency domain. Frequency analysis also simplifies the understanding and interpretation of the effects of various time-domain operations, both linear and non-linear. For instance, only non-linear operations
can create new frequencies in the frequency spectrum.
The Fourier transform of a stochastic
(random) waveform (noise
) is also random. Some kind of averaging is required in order to create a clear picture of the underlying frequency content (frequency distribution
). Typically, the data is divided into time-segments of a chosen duration, and transforms are performed on each one. Then the magnitude or (usually) squared-magnitude components of the transforms are summed into an average transform. This is a very common operation performed on digitally sampled
time-domain data, using the discrete Fourier transform
. This type of processing is called Welch's method. When the result is flat, it is commonly referred to as white noise
. However, such processing techniques often reveal spectral content even among data which appears noisy in the time domain.
or quality of a sound
or note
. It is the relative strength of pitches called harmonic
s and partial
s (collectively overtone
s) at various frequencies usually above the fundamental frequency, which is the actual note named (e.g. an A).
The spectrum analyzer
is an instrument which can be used to convert the sound wave
of the musical note into a visual display of the constituent frequencies. This visual display is referred to as an acoustic spectrogram
. Software based audio spectrum analyzers are available at low cost, providing easy access not only to industry professionals, but also to academics, students and the hobbyist. The acoustic spectrogram generated by the spectrum analyzer provides an acoustic signature
of the musical note. In addition to revealing the fundamental frequency and its overtones, the spectrogram is also useful for analysis of the temporal attack, decay, sustain, and release of the musical note.
Frequency domain
In electronics, control systems engineering, and statistics, frequency domain is a term used to describe the domain for analysis of mathematical functions or signals with respect to frequency, rather than time....
. The frequency spectrum can be generated via a Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of the signal, and the resulting values are usually presented as amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
and phase
Phase (waves)
Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
, both plotted versus frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
.
Any signal that can be represented as an amplitude that varies with time has a corresponding frequency spectrum. This includes familiar concepts such as visible light (color
Color
Color or colour is the visual perceptual property corresponding in humans to the categories called red, green, blue and others. Color derives from the spectrum of light interacting in the eye with the spectral sensitivities of the light receptors...
), musical notes, radio/TV channels
Radio frequency
Radio frequency is a rate of oscillation in the range of about 3 kHz to 300 GHz, which corresponds to the frequency of radio waves, and the alternating currents which carry radio signals...
, and even the regular rotation of the earth. When these physical phenomena are represented in the form of a frequency spectrum, certain physical descriptions of their internal processes become much simpler. Often, the frequency spectrum clearly shows harmonics, visible as distinct spikes or lines, that provide insight into the mechanisms that generate the entire signal.
Light
A source of light can have many colors mixed together and in different amounts (intensities). A rainbow, or prism, sends the different frequencies in different directions, making them individually visible at different angles. A graph of the intensity plotted against the frequency (showing the amount of each color) is the frequency spectrum of the light. When all the visible frequencies are present in equal amounts, the perceived color of the light is white, and the spectrum is a flat line. Therefore, flat-line spectrums in general are often referred to as white, whether they represent light or something else.Sound
Similarly, a source of sound can have many different frequencies mixed together. A musical tone's
Musical tone
A musical tone is a steady periodic sound. A musical tone is characterized by its duration, pitch, intensity , and timbre . The notes used in music can be more complex than musical tones, as they may include aperiodic aspects, such as attack transients, vibrato, and envelope modulation.A simple...
timbre
Timbre
In music, timbre is the quality of a musical note or sound or tone that distinguishes different types of sound production, such as voices and musical instruments, such as string instruments, wind instruments, and percussion instruments. The physical characteristics of sound that determine the...
is characterized by its harmonic
Harmonic
A harmonic of a wave is a component frequency of the signal that is an integer multiple of the fundamental frequency, i.e. if the fundamental frequency is f, the harmonics have frequencies 2f, 3f, 4f, . . . etc. The harmonics have the property that they are all periodic at the fundamental...
spectrum
Harmonic spectrum
A harmonic spectrum is a spectrum containing only frequency components whose frequencies are whole number multiples of the fundamental frequency; such frequencies are known as harmonics....
. Sound in our environment that we refer to as noise includes many different frequencies. When a sound signal contains a mixture of all audible frequencies, distributed equally over the audio spectrum, it is called white noise
White noise
White noise is a random signal with a flat power spectral density. In other words, the signal contains equal power within a fixed bandwidth at any center frequency...
.
Radio
In radio and telecommunications, the frequency spectrum can be shared among many different broadcasters. Each broadcast radio and TV station transmits a wave on an assigned frequency range, called a channel. When many broadcasters are present, the radio spectrum consists of the sum of all the individual channels, each carrying separate information, spread across a wide frequency spectrum. Any particular radio receiver will detect a single function of amplitude (voltage) vs. time. The radio then uses a tuned circuit or tuner to select a single channel or frequency band and demodulateModulation
In electronics and telecommunications, modulation is the process of varying one or more properties of a high-frequency periodic waveform, called the carrier signal, with a modulating signal which typically contains information to be transmitted...
or decode the information from that broadcaster. If we made a graph of the strength of each channel vs. the frequency of the tuner, it would be the frequency spectrum of the antenna signal.
Spectrum analysis
Spectrum analysis can be performed on the entire signal. Alternatively, a signal can be broken into short segments (sometimes called frames), and spectrum analysis may be applied to these individual segments. Periodic function
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
s (such as
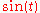) are particularly well-suited for this sub-division. General mathematical techniques for analyzing non-periodic functions fall into the category of Fourier analysis.The Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of a function produces a frequency spectrum which contains all of the information about the original signal, but in a different form. This means that the original function can be completely reconstructed (synthesized) by an inverse Fourier transform. For perfect reconstruction, the spectrum analyzer must preserve both the amplitude and phase
Phase (waves)
Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
of each frequency component. These two pieces of information can be represented as a 2-dimensional vector, as a complex number, or as magnitude (amplitude) and phase in polar coordinates. A common technique in signal processing is to consider the squared amplitude, or power
Power (physics)
In physics, power is the rate at which energy is transferred, used, or transformed. For example, the rate at which a light bulb transforms electrical energy into heat and light is measured in watts—the more wattage, the more power, or equivalently the more electrical energy is used per unit...
; in this case the resulting plot is referred to as a power spectrum.
In practice, nearly all software and electronic devices that generate frequency spectra apply a fast Fourier transform
Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
(FFT), which is a specific mathematical approximation to the full integral solution. Formally stated, the FFT is a method for computing the discrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
of a sampled signal
Sampling (signal processing)
In signal processing, sampling is the reduction of a continuous signal to a discrete signal. A common example is the conversion of a sound wave to a sequence of samples ....
.
Because of reversibility, the Fourier transform is called a representation of the function, in terms of frequency instead of time; thus, it is a frequency domain
Frequency domain
In electronics, control systems engineering, and statistics, frequency domain is a term used to describe the domain for analysis of mathematical functions or signals with respect to frequency, rather than time....
representation. Linear operations that could be performed in the time domain have counterparts that can often be performed more easily in the frequency domain. Frequency analysis also simplifies the understanding and interpretation of the effects of various time-domain operations, both linear and non-linear. For instance, only non-linear operations
Nonlinearity
In mathematics, a nonlinear system is one that does not satisfy the superposition principle, or one whose output is not directly proportional to its input; a linear system fulfills these conditions. In other words, a nonlinear system is any problem where the variable to be solved for cannot be...
can create new frequencies in the frequency spectrum.
The Fourier transform of a stochastic
Stochastic
Stochastic refers to systems whose behaviour is intrinsically non-deterministic. A stochastic process is one whose behavior is non-deterministic, in that a system's subsequent state is determined both by the process's predictable actions and by a random element. However, according to M. Kac and E...
(random) waveform (noise
Noise
In common use, the word noise means any unwanted sound. In both analog and digital electronics, noise is random unwanted perturbation to a wanted signal; it is called noise as a generalisation of the acoustic noise heard when listening to a weak radio transmission with significant electrical noise...
) is also random. Some kind of averaging is required in order to create a clear picture of the underlying frequency content (frequency distribution
Frequency distribution
In statistics, a frequency distribution is an arrangement of the values that one or more variables take in a sample. Each entry in the table contains the frequency or count of the occurrences of values within a particular group or interval, and in this way, the table summarizes the distribution of...
). Typically, the data is divided into time-segments of a chosen duration, and transforms are performed on each one. Then the magnitude or (usually) squared-magnitude components of the transforms are summed into an average transform. This is a very common operation performed on digitally sampled
Sampling (signal processing)
In signal processing, sampling is the reduction of a continuous signal to a discrete signal. A common example is the conversion of a sound wave to a sequence of samples ....
time-domain data, using the discrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
. This type of processing is called Welch's method. When the result is flat, it is commonly referred to as white noise
White noise
White noise is a random signal with a flat power spectral density. In other words, the signal contains equal power within a fixed bandwidth at any center frequency...
. However, such processing techniques often reveal spectral content even among data which appears noisy in the time domain.
Physical acoustics of music
Sound spectrum is one of the determinants of the timbreTimbre
In music, timbre is the quality of a musical note or sound or tone that distinguishes different types of sound production, such as voices and musical instruments, such as string instruments, wind instruments, and percussion instruments. The physical characteristics of sound that determine the...
or quality of a sound
Sound
Sound is a mechanical wave that is an oscillation of pressure transmitted through a solid, liquid, or gas, composed of frequencies within the range of hearing and of a level sufficiently strong to be heard, or the sensation stimulated in organs of hearing by such vibrations.-Propagation of...
or note
Note
In music, the term note has two primary meanings:#A sign used in musical notation to represent the relative duration and pitch of a sound;#A pitched sound itself....
. It is the relative strength of pitches called harmonic
Harmonic
A harmonic of a wave is a component frequency of the signal that is an integer multiple of the fundamental frequency, i.e. if the fundamental frequency is f, the harmonics have frequencies 2f, 3f, 4f, . . . etc. The harmonics have the property that they are all periodic at the fundamental...
s and partial
Partial
Partial may refer to:*partial derivative, in mathematics** ∂, the partial derivative symbol, often read as "partial"*partial function, in mathematics*partial algorithm, in computer science*part score, in contract bridge...
s (collectively overtone
Overtone
An overtone is any frequency higher than the fundamental frequency of a sound. The fundamental and the overtones together are called partials. Harmonics are partials whose frequencies are whole number multiples of the fundamental These overlapping terms are variously used when discussing the...
s) at various frequencies usually above the fundamental frequency, which is the actual note named (e.g. an A).
The spectrum analyzer
Spectrum analyzer
A spectrum analyzer measures the magnitude of an input signal versus frequency within the full frequency range of the instrument. The primary use is to measure the power of the spectrum of known and unknown signals...
is an instrument which can be used to convert the sound wave
Sound
Sound is a mechanical wave that is an oscillation of pressure transmitted through a solid, liquid, or gas, composed of frequencies within the range of hearing and of a level sufficiently strong to be heard, or the sensation stimulated in organs of hearing by such vibrations.-Propagation of...
of the musical note into a visual display of the constituent frequencies. This visual display is referred to as an acoustic spectrogram
Spectrogram
A spectrogram is a time-varying spectral representation that shows how the spectral density of a signal varies with time. Also known as spectral waterfalls, sonograms, voiceprints, or voicegrams, spectrograms are used to identify phonetic sounds, to analyse the cries of animals; they were also...
. Software based audio spectrum analyzers are available at low cost, providing easy access not only to industry professionals, but also to academics, students and the hobbyist. The acoustic spectrogram generated by the spectrum analyzer provides an acoustic signature
Acoustic signature
Acoustic signature is used to describe a combination of acoustic emissions of ships and submarines.-Contributing factors:The acoustic signature is made up of a number of individual elements...
of the musical note. In addition to revealing the fundamental frequency and its overtones, the spectrogram is also useful for analysis of the temporal attack, decay, sustain, and release of the musical note.
See also
- Frequency estimationFrequency estimationFrequency estimation is the process of estimating the complex frequency components of a signal in the presence of noise. The most common methods involve identifying the noise subspace to extract these components...
- Electromagnetic spectrumElectromagnetic spectrumThe electromagnetic spectrum is the range of all possible frequencies of electromagnetic radiation. The "electromagnetic spectrum" of an object is the characteristic distribution of electromagnetic radiation emitted or absorbed by that particular object....