Finite potential barrier (QM) - AbsoluteAstronomy.com

Quantum mechanics

Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...

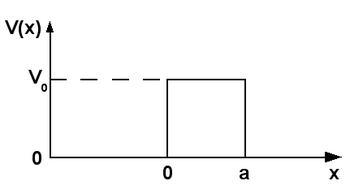
, the rectangular potential barrier is a standard one-dimensional problem that demonstrates the phenomena of wave-mechanical tunneling (also called "quantum tunneling") and wave-mechanical reflection. The problem consists of solving the one-dimensional time-independent Schrödinger equation

Schrödinger equation

The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....

for a particle encountering a rectangular potential

Potential

*In linguistics, the potential mood*The mathematical study of potentials is known as potential theory; it is the study of harmonic functions on manifolds...

energy barrier. It is usually assumed, as here, that a free particle

Free particle

In physics, a free particle is a particle that, in some sense, is not bound. In classical physics, this means the particle is present in a "field-free" space.-Classical Free Particle:The classical free particle is characterized simply by a fixed velocity...

impinges on the barrier from the left.

Although a particle hypothetically behaving as a point mass would be reflected, a particle actually behaving as a matter wave has a finite probability that it will penetrate the barrier and continue its travel as a wave on the other side. In classical wave-physics, this effect is known as evanescent wave coupling. The likelihood that the particle will pass through the barrier is given by the transmission coefficient

Transmission coefficient

The transmission coefficient is used in physics and electrical engineering when wave propagation in a medium containing discontinuities is considered...

, whereas the likelihood that it is reflected is given by the reflection coefficient. Schrödinger's wave-equation

Schrödinger equation

allows these coefficients to be calculated.

Calculation

The time-independent Schrödinger equation for the wave function

reads

where

is the Hamiltonian

Hamiltonian (quantum mechanics)

In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...

is the (reduced)
Planck constant

Planck constant

The Planck constant , also called Planck's constant, is a physical constant reflecting the sizes of energy quanta in quantum mechanics. It is named after Max Planck, one of the founders of quantum theory, who discovered it in 1899...

is the mass

Mass

Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...

the energy of the particle and

is the barrier potential with height

and width

is the Heaviside step function

Heaviside step function

The Heaviside step function, or the unit step function, usually denoted by H , is a discontinuous function whose value is zero for negative argument and one for positive argument....

.

The barrier is positioned between

and

. Without
changing the results, any other shifted position was possible.
The first term in the Hamiltonian,

is the kinetic energy.

The barrier divides the space in three parts (

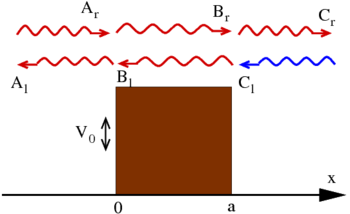
). In any of these parts, the potential is constant, meaning that the particle is quasi-free, and the solution of the Schrödinger equation can be written as a superposition

Quantum superposition

Quantum superposition is a fundamental principle of quantum mechanics. It holds that a physical system exists in all its particular, theoretically possible states simultaneously; but, when measured, it gives a result corresponding to only one of the possible configurations.Mathematically, it...

of left and right moving waves (see free particle

Free particle

). If

where the wave numbers are related to the energy via

.

The index r/l on the coefficients A and B denotes the direction of the velocity vector. Note that, if the energy of the particle is below the barrier height,

becomes imaginary and the wave function is exponentially decaying within the barrier. Nevertheless, we keep the notation r/l even though the waves are not propagating anymore in this case. Here we assumed

. The case

is treated below.

The coefficients

have to be found from the boundary conditions of the wave function at

and

. The wave function and its derivative have to be continuous

Continuous function

In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...

everywhere, so.

.

Inserting the wave functions, the boundary conditions give the following restrictions on the coefficients

E = V₀

If the energy equals the barrier height, the solutions of the Schrödinger equation in the barrier region are not exponentials anymore but linear functions of the space coordinate

The complete solution of the Schrödinger equation is found in the same way as above by matching wave functions and their derivatives at

and

. That results in the following restrictions on the coefficients:

Transmission and reflection

At this point, it is instructive to compare the situation to the classical case. In both cases, the particle behaves as a free particle outside of the barrier region. A classical particle with energy

larger than the barrier height

would always pass the barrier, and a classical particle with

incident on the barrier would always get reflected.

To study the quantum case, consider the following situation: a particle incident on the barrier from the left side (

). It may be reflected (

) or transmitted (

).

To find the amplitudes for reflection and transmission for incidence from the left, we put in the above equations

(incoming particle),

(reflection),

=0 (no incoming particle from the right), and

(transmission). We then eliminate the coefficients

from the equation and solve for

and

.

The result is:

Due to the mirror symmetry

Symmetry

Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...

of the model, the amplitudes for incidence from the right are the same as those from the left. Note that these expressions hold for any energy

E < V₀

The surprising result is that for energies less than the barrier height,

there is a non-zero probability

for the particle to be transmitted through the barrier, being

. This effect, which differs from the classical case, is called quantum tunneling. The transmission is exponentially suppressed with the barrier width, which can be understood from the functional form of the wave function: Outside of the barrier it oscillates with wave vector

, whereas within the barrier it is exponentially damped over a distance

. If the barrier is much larger than this decay length, the left and right part are virtually independent and tunneling as a consequence is suppressed.

E > V₀

In this case

Equally surprising is that for energies larger than the barrier height,

, the particle may be reflected from the barrier with a non-zero probability

This reflection probability is in fact oscillating with

and only in the limit

approaches the classical result

, no reflection. Note that the probabilities and amplitudes as written are for any energy (above/below) the barrier height.

E = V₀

The transmission probability at

evaluates to

Remarks and applications

The calculation presented above may at first seem unrealistic and hardly
useful. However it has proved to be a suitable model for a variety of real-life
systems. One such example are interfaces between two conducting materials. In the bulk of the materials, the motion of the electrons is quasi-free and can be described by the kinetic term in the above Hamiltonian with an effective mass

Effective mass

In solid state physics, a particle's effective mass is the mass it seems to carry in the semiclassical model of transport in a crystal. It can be shown that electrons and holes in a crystal respond to electric and magnetic fields almost as if they were particles with a mass dependence in their...

. Often the surfaces of such materials are covered with oxide layers or are not ideal for other reasons. This thin, non-conducting layer may then be modeled by a barrier potential as above. Electrons may then tunnel from one material to the other giving rise to a current.

The operation of a scanning tunneling microscope

Scanning tunneling microscope

A scanning tunneling microscope is an instrument for imaging surfaces at the atomic level. Its development in 1981 earned its inventors, Gerd Binnig and Heinrich Rohrer , the Nobel Prize in Physics in 1986. For an STM, good resolution is considered to be 0.1 nm lateral resolution and...

(STM) relies on this tunneling effect. In that case, the barrier is due to the gap between the tip of the STM and the underlying object. Since the tunnel current depends exponentially on the barrier width, this device is extremely sensitive to height variations on the examined sample.

The above model is one-dimensional, while space is three-dimensional. One should solve the Schrödinger equation in three dimensions. On the other hand, many systems only change along one coordinate direction and are translationally invariant along the others. The Schrödinger equation may then be reduced to the case considered here by an ansatz for the wave function of the type:

.

For another, related model of a barrier, see Delta potential barrier (QM), which can be regarded as a special case of the finite potential barrier. All results from this article immediately apply to the delta potential barrier's taking the limits