Exact cover
Encyclopedia
In mathematics
, given a collection
of subset
s of a set X, an exact cover is a subcollection
of 
such that each element in X is contained in exactly one subset in 
.
One says that each element in X is covered by exactly one subset in
.
An exact cover is a kind of cover
.
In computer science
, the exact cover problem is a decision problem
to find an exact cover or else determine none exists.
The exact cover problem is NP-complete
and is one of Karp's 21 NP-complete problems
.
The exact cover problem is a kind of constraint satisfaction problem
.
An exact cover problem can be represented by an incidence matrix
or a bipartite graph
.
Knuth's Algorithm X
is an algorithm
that finds all solutions to an exact cover problem. Dancing Links
, commonly known as DLX, is the technique suggested by Donald Knuth
to efficiently implement his Algorithm X on a computer.
The standard exact cover problem can be generalized slightly to involve not only "exactly one" constraints but also "at-most-one" constraints.
Finding Pentomino
tilings and solving Sudoku
are noteworthy examples of exact cover problems.
The N queens problem is a slightly generalized exact cover problem.
of subset
s of a set X, an exact cover of X is a subcollection
of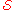 
that satisfies two conditions:
In short, an exact cover is "exact" in the sense that each element in X is contained in exactly one subset in
.
Equivalently, an exact cover of X is a subcollection
of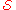 
that partitions
X.
For an exact cover of X to exist, it is necessary that:
If the empty set
∅ is contained in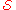
, then it makes no difference whether or not it is in any exact cover.
Thus it is typical to assume that:
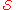= {N, O, E, P} be a collection of subsets of a set X = {1, 2, 3, 4} such that:
The subcollection {O, E} is an exact cover of X, since the subsets O = {1, 3} and E = {2, 4} are disjoint and their union is X = {1, 2, 3, 4}.
The subcollection {N, O, E} is also an exact cover of X.
Including the empty set N = { } makes no difference, as it is disjoint with all subsets and does not change the union.
The subcollection {E, P} is not an exact cover of X.
The intersection of the subsets E and P, {2}, is not empty:
The subsets E and P are not disjoint.
Moreover, the union of the subsets E and P, {2, 3, 4}, is not X = {1, 2, 3, 4}:
Neither E nor P covers the element 1.
On the other hand, there is no exact cover—indeed, not even a cover—of Y = {1, 2, 3, 4, 5} because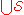
= {1, 2, 3, 4} is a proper subset of Y:
None of the subsets in
contains the element 5.
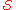= {A, B, C, D, E, F} be a collection of subsets
of a set X = {1, 2, 3, 4, 5, 6, 7} such that:
Then the subcollection
= {B, D, F} is an exact cover, since each element in X is contained in exactly one of the subsets:
Moreover, {B, D, F} is the only exact cover, as the following argument demonstrates:
Because A and B are the only subsets containing 1, an exact cover must contain A or B, but not both.
If an exact cover contains A, then it doesn't contain B, C, E, or F, as each of these subsets has an element in common with A.
Then D is the only remaining subset, but the collection {A, D} doesn't cover the element 2.
In conclusion, there is no exact cover containing A.
On the other hand, if an exact cover contains B, then it doesn't contain A or C, as each of these subsets has an element in common with B.
Because D is the only remaining subset containing 5, D must be part of the exact cover.
If an exact cover contains D, then it doesn't contain E, as E has an element in common with D.
Then F is the only remaining subset, and the collection {B, D, F} is indeed an exact cover.
See the example in the article on Knuth's Algorithm X
for a matrix-based version of this argument.
"contains" between subsets in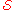
and elements in X.
There are different equivalent ways to represent this relation.
For example, the detailed example above uses this standard representation:
Again, the subcollection
= {B, D, F} is an exact cover, since each element is contained in exactly one selected subset, as the highlighting makes clear.
, listing the subsets each element is contained in.
For example, the relation "contains" in the detailed example above can be represented by listing the subsets each element is contained in:
Again, the subcollection
= {B, D, F} is an exact cover, since each element is contained in exactly one selected subset, as the highlighting makes clear.
When solving an exact cover problem, it is often useful to switch between the standard and inverse representations.
.
The matrix includes one row for each subset in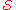
and one column for each element in X.
The entry in a particular row and column is 1 if the corresponding subset contains the corresponding element, and is 0 otherwise.
As each row represents the elements contained in the corresponding subset and each column represents the subsets containing the corresponding element, an incidence matrix effectively provides both the standard and inverse representations.
In the matrix representation, an exact cover is a selection of rows such that each column contains a 1 in exactly one selected row.
For example, the relation "contains" in the detailed example above can be represented by a 6×7 incidence matrix:
Again, the subcollection
= {B, D, F} is an exact cover, since each element is contained in exactly one selected subset, i.e., each column contains a 1 in exactly one selected row, as the highlighting makes clear.
See the example in the article on Knuth's Algorithm X
for a matrix-based solution to the detailed example above.
In turn, the incidence matrix can be seen also as describing a hypergraph
. The hypergraph includes one node for each element in X and one edge for each subset in
; each node is included in exactly one of the edges forming the cover.
.
The vertices of the graph are divided into two disjoint sets, one representing the subsets in
and another representing the elements in X.
If a subset contains an element, an edge connects the corresponding vertices in the graph.
In the graph representation, an exact cover is a selection of vertices corresponding to subsets such that each vertex corresponding to an element is connected to exactly one selected vertex.
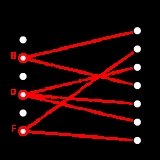
For example, the relation "contains" in the detailed example above can be represented by a bipartite graph with 6+7 = 13 vertices:
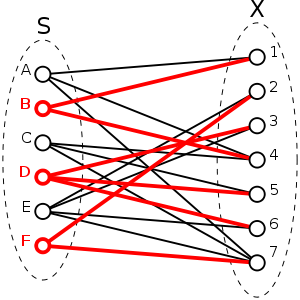Again, the subcollection 
= {B, D, F} is an exact cover, since each element is contained in exactly one selected subset, i.e., the vertex corresponding to each element in X is connected to exactly one selected vertex, as the highlighting makes clear.
of subsets of a set X, the logic does not depend on the presence of subsets containing elements.
An "abstract exact cover problem" arises whenever there is a binary relation
between two sets P and Q and the goal is to select a subset P* of P such that each element in Q is related to exactly one element in P*.
In general, the elements of P represent choices and the elements of Q represent "exactly one" constraints on those choices.
More formally, given a binary relation R
P × Q between sets P and Q, one can call a subset P* of P an "abstract exact cover" of Q if each element in Q is R -1-related to exactly one element in P*.
Here R -1 is the inverse
of R.
In general, R -1 restricted to Q × P* is a function
from Q to P*, which maps each element in Q to the unique element in P* that is R-related that element in Q.
This function is onto, unless P* contains the "empty set," i.e., an element which isn't R-related to any element in Q.
In the canonical exact cover problem, P is a collection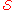
of subsets of X, Q is the set X, R is the binary relation "contains" between subsets and elements, and R -1 restricted to Q × P* is the function "is contained in" from elements to selected subsets.
, given a collection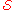
of subsets of a set X, an exact hitting set X* is a subset of X such that each subset in 
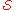contains exactly one element in X*. One says that each subset in 
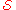is hit by exactly one element in X*.
In computer science
, the exact hitting set problem is a decision problem
to find an exact hitting set or else determine none exists.
The exact hitting set problem is an abstract exact cover problem.
In the notation above, P is the set X, Q is a collection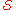
of subsets of X, R is the binary relation "is contained in" between elements and subsets, and R -1 restricted to Q × P* is the function "contains" from subsets to selected elements.
Whereas an exact cover problem involves selecting subsets and the relation "contains" from subsets to elements, an exact hitting set problem involves selecting elements and the relation "is contained in" from elements to subsets.
In a sense, an exact hitting set problem is the inverse of the exact cover problem involving the same set and collection of subsets.
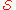= {A, B, C, D, E, F} be a collection of subsets of a set X = {1, 2, 3, 4, 5, 6, 7} such that:
Then X* = {1, 2, 5} is an exact hitting set, since each subset in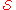
contains exactly one element in X*, as the highlighting makes clear.
Moreover, {1, 2, 5} is the only exact hitting set, as the following argument demonstrates:
Because 2 and 7 are the only elements that hit F, an exact hitting set must contain 2 or 7, but not both.
If an exact hitting set contains 7, then it doesn't contain 1, 2, 3, 4, 5, or 6, as each of these elements are contained in some subset also containing 7.
Then there are no more remaining elements, but {7} is not an exactly hitting set, as it doesn't hit B or D.
In conclusion, there is no exact hitting set containing 7.
On the other hand, if an exact hitting set contains 2, then it doesn't contain 3, 6, or 7, as each of these elements are contained in some subset also containing 2.
Because 5 is the only remaining element that hits D, the exact hitting set must contain 5.
If an exact hitting set contains 5, then it doesn't contain 4, as both hit C.
Because 1 is the only remaining element that hits A, the exact hitting set must contain 1.
Then there are no more remaining elements, and {1, 2, 5} is indeed an exact hitting set.
Although this example involves the same collection of subsets as the detailed exact cover example above, it is essentially a different problem. In a sense, the exact hitting set problem is the inverse (or transpose or converse) of the corresponding exact cover problem above, as the matrix representation makes clear:
For example, as the subset B contains the elements 1 and 4 in the exact cover problem, the subsets I and IV contain the element b in the dual exact hitting set problem.
In particular, let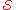
= {I, II, III, IV, V, VI, VII} be a collection of subsets of a set X = {a, b, c, d, e, f} such that:
Then X* = {b, d, f} is an exact hitting set, since each subset in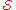
contains (is hit by) exactly one element in X*, as the highlighting makes clear.
The exact hitting set X* = {b, d, f} here is essentially the same as the exact cover
= {B, D, F} above, as the matrix representation makes clear:
is a recursive
, nondeterministic, depth-first, backtracking
algorithm
that finds all solutions to the exact cover problem.
Dancing Links
, commonly known as DLX, is the technique suggested by Donald Knuth
to efficiently implement his Algorithm X on a computer.
Dancing Links uses the matrix representation of the problem.
Dancing Links implements the matrix as a series of doubly linked lists of the 1s of the matrix:
each 1 element has a link to the next 1 above, below, to the left, and to the right of itself.
It is a simple generalization to relax this requirement slightly and allow for the possibility that some "primary" constraints must be satisfied by exactly one selection but other "secondary" constraints can be satisfied by at most one selection.
As Knuth explains, a generalized exact cover problem can be converted to an equivalent exact cover problem by simply appending one row for each secondary column, containing a single 1 in that column. If in a particular candidate solution a particular secondary column is satisfied, then the added row isn't needed.
But if the secondary column isn't satisfied, as is allowed in the generalized problem but not the standard problem, then the added row can be selected to ensure the column is satisfied.
But Knuth goes on to explain that it is better working with the generalized problem directly, because the generalized algorithm is simpler and faster:
A simple change to his Algorithm X allows secondary columns to be handled directly.
The N queens problem is an example of a generalized exact cover problem, as the constraints corresponding to the diagonals of the chessboard need not be satisfied.
to exact cover problems, which then can be solved with techniques such as Dancing Links.
However, for some well known problems, the reduction is particularly direct.
For instance, the problem of tiling a board with pentominoes, and solving Sudoku
can both be viewed as exact cover problems.
explains in his paper "Dancing links."
For example, consider the problem of tiling with pentominoes an 8×8 chessboard with the 4 central squares removed:
The problem involves two kinds of constraints:
Thus there are 12+60 = 72 constraints in all.
As both kinds of constraints are "exactly one" constraints, the problem is an exact cover problem.
The problem involves many choices, one for each way to place a pentomino on the board.
It is convenient to consider each choice as a sets of 6 constraints: 1 constraint for the pentomino being placed and 5 constraints for the five squares where it is placed.
In the case of an 8×8 chessboard with the 4 central squares removed, there are 1568 such choices, for example:
One of many solutions of this exact cover problem is the following set of 12 choices:
This set of choices corresponds to the following solution to the pentomino tiling problem:
A pentomino tiling problem is more naturally viewed as an exact cover problem than an exact hitting set problem, because it is more natural to view each choice as a set of constraints than each constraint as a set of choices.
Each choice is related to just 6 constraints, which are easy to enumerate. On the other hand, each constraint is related to many choices, which are harder to enumerate.
Whether viewed as an exact cover problem or an exact hitting set problem, the matrix representation is the same, having 1568 rows corresponding to choices and 72 columns corresponding to constraints.
Each row contains a single 1 in the column identifying the pentomino and five 1s in the columns identifying the squares covered by the pentomino.
Using the matrix, a computer can find all solutions relatively quickly, for example, using Dancing Links
.
See also Solving Pentomino Puzzles with Backtracking.
is to assign numbers (or digits, values, symbols) to cells (or squares) in a grid so as to satisfy certain constraints.
In the standard 9×9 Sudoku variant, there are four kinds of constraints:
While the first constraint might seem trivial, it is nevertheless needed to ensure there is only one number per cell. Intuitively, placing a number into a cell prohibits placing that number in any other cell sharing the same column, row, or box and also prohibits placing any other number into the now occupied cell.
Solving Sudoku is an exact cover problem.
More precisely, solving Sudoku is an exact hitting set problem, which is equivalent to an exact cover problem (as in Example 5 above), when viewed as a problem to select possibilities such that each constraint set contains (i.e., is hit by) exactly one selected possibility.
In the notation above for the (generalized) exact cover problem, X is the set of possibilities, Y is a set of constraint sets, and R is the binary relation "is contained in."
Each possible assignment of a particular number to a particular cell is a possibility (or candidate).
When Sudoku is played with pencil and paper, possibilities are often called pencil marks.
In the standard 9×9 Sudoku variant, in which each of 9×9 cells is assigned one of 9 numbers, there are 9×9×9=729 possibilities.
Using obvious notation for rows, columns and numbers, the possibilities can be labeled
The fact that each kind of constraint involves exactly one of something is what makes Sudoku an exact hitting set problem.
The constraints can be represented by constraint sets.
The problem is to select possibilities such that each constraint set contains (i.e., is hit by) exactly one selected possibility.
In the standard 9×9 Sudoku variant, there are four kinds of constraints sets corresponding to the four kinds of constraints:
Since there are 9 rows, 9 columns, 9 boxes and 9 numbers, there are 9×9=81 row-column constraint sets, 9×9=81 row-number constraint sets, 9×9=81 column-number constraint sets, and 9×9=81 box-number constraint sets: 81+81+81+81=324 constraint sets in all.
In brief, the standard 9×9 Sudoku variant is an exact hitting set problem with 729 possibilities and 324 constraint sets.
Thus the problem can be represented by a 729×324 matrix.
Although it is difficult to present the entire 729×324 matrix, the general nature of the matrix can be seen from several snapshots:
The complete 729×324 matrix is available from Bob Hanson.
Note that the set of possibilities RxCy#z can be arranged as a 9×9×9 cube in a 3-dimensional space with coordinates x, y, and z.
Then each row Rx, column Cy, or number #z is a 9×9×1 "slice" of possibilities; each box Bw is a 9x3×3 "tube" of possibilities; each row-column constraint set RxCy, row-number constraint set Rx#z, or column-number constraint set Cy#z is a 9x1×1 "strip" of possibilities; each box-number constraint set Bw#z is a 3x3×1 "square" of possibilities; and each possibility RxCy#z is a 1x1×1 "cubie" consisting of a single possibility.
Moreover, each constraint set or possibility is the intersection
of the component sets.
For example, R1C2#3 = R1 ∩ C2 ∩ #3, where ∩ denotes set intersection.
Although other Sudoku variations have different numbers of rows, columns, numbers and/or different kinds of constraints, they all involve possibilities and constraint sets, and thus can be seen as exact hitting set problems.
The N queens problem is an example of a generalized exact cover problem. The problem involves four kinds of constraints:
Note that the 2N rank and file constraints form the primary constraints, while the 4N - 2 diagonal and reverse diagonals form the secondary constraints. Further, because the each of first and last diagonal and reverse diagonals involve only one square on the chessboard, these can be omitted and thus we can reduce the number of secondary constraints to 4N - 6. The matrix for the N queens problem then have N2 rows and 6N - 6 columns, each row for a possible queen placement on each square on the chessboard, and each column for each constraint.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, given a collection
of subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of a set X, an exact cover is a subcollection
of such that each element in X is contained in exactly one subset in .One says that each element in X is covered by exactly one subset in
.An exact cover is a kind of cover
Cover (topology)
In mathematics, a cover of a set X is a collection of sets whose union contains X as a subset. Formally, ifC = \lbrace U_\alpha: \alpha \in A\rbrace...
.
In computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, the exact cover problem is a decision problem
Decision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
to find an exact cover or else determine none exists.
The exact cover problem is NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
and is one of Karp's 21 NP-complete problems
Karp's 21 NP-complete problems
One of the most important results in computational complexity theory was Stephen Cook's 1971 demonstration of the first NP-complete problem, the boolean satisfiability problem...
.
The exact cover problem is a kind of constraint satisfaction problem
Constraint satisfaction problem
Constraint satisfaction problems s are mathematical problems defined as a set of objects whose state must satisfy a number of constraints or limitations. CSPs represent the entities in a problem as a homogeneous collection of finite constraints over variables, which is solved by constraint...
.
An exact cover problem can be represented by an incidence matrix
Incidence matrix
In mathematics, an incidence matrix is a matrix that shows the relationship between two classes of objects. If the first class is X and the second is Y, the matrix has one row for each element of X and one column for each element of Y. The entry in row x and column y is 1 if x and y are related ...
or a bipartite graph
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
.
Knuth's Algorithm X
Knuth's Algorithm X
Donald Knuth's Algorithm X is a recursive, nondeterministic, depth-first, backtracking algorithm that finds all solutions to the exact cover problem represented by a matrix A consisting of 0s and 1s...
is an algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
that finds all solutions to an exact cover problem. Dancing Links
Dancing Links
In computer science, Dancing Links, also known as DLX, is the technique suggested by Donald Knuth to efficiently implement his Algorithm X. Algorithm X is a recursive, nondeterministic, depth-first, backtracking algorithm that finds all solutions to the exact cover problem...
, commonly known as DLX, is the technique suggested by Donald Knuth
Donald Knuth
Donald Ervin Knuth is a computer scientist and Professor Emeritus at Stanford University.He is the author of the seminal multi-volume work The Art of Computer Programming. Knuth has been called the "father" of the analysis of algorithms...
to efficiently implement his Algorithm X on a computer.
The standard exact cover problem can be generalized slightly to involve not only "exactly one" constraints but also "at-most-one" constraints.
Finding Pentomino
Pentomino
A pentomino is a polyomino composed of five congruent squares, connected along their edges ....
tilings and solving Sudoku
Sudoku
is a logic-based, combinatorial number-placement puzzle. The objective is to fill a 9×9 grid with digits so that each column, each row, and each of the nine 3×3 sub-grids that compose the grid contains all of the digits from 1 to 9...
are noteworthy examples of exact cover problems.
The N queens problem is a slightly generalized exact cover problem.
Formal definition
Given a collection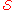 of subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of a set X, an exact cover of X is a subcollection
of 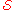that satisfies two conditions:
- The intersectionIntersection (set theory)In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of any two distinct subsets in
is emptyEmpty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
, i.e., the subsets in
are pairwise disjoint. In other words, each element in X is contained in at most one subset in 
. - The unionUnion (set theory)In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of the subsets in
is X, i.e., the subsets in 
coverCover (topology)In mathematics, a cover of a set X is a collection of sets whose union contains X as a subset. Formally, ifC = \lbrace U_\alpha: \alpha \in A\rbrace...
X. In other words, each element in X is contained in at least one subset in
.
In short, an exact cover is "exact" in the sense that each element in X is contained in exactly one subset in
.Equivalently, an exact cover of X is a subcollection
of 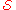that partitionsPartition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
X.
For an exact cover of X to exist, it is necessary that:
- The union of the subsets in
is X. In other words, each element in X is contained in at least one subset in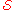 
.
If the empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
∅ is contained in
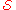, then it makes no difference whether or not it is in any exact cover.Thus it is typical to assume that:
- The empty set is not in
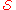. In other words, each subset in 
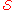contains at least one element.
Basic examples
Let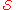 = {N, O, E, P} be a collection of subsets of a set X = {1, 2, 3, 4} such that:
- N = { },
- O = {1, 3},
- E = {2, 4}, and
- P = {2, 3}.
The subcollection {O, E} is an exact cover of X, since the subsets O = {1, 3} and E = {2, 4} are disjoint and their union is X = {1, 2, 3, 4}.
The subcollection {N, O, E} is also an exact cover of X.
Including the empty set N = { } makes no difference, as it is disjoint with all subsets and does not change the union.
The subcollection {E, P} is not an exact cover of X.
The intersection of the subsets E and P, {2}, is not empty:
The subsets E and P are not disjoint.
Moreover, the union of the subsets E and P, {2, 3, 4}, is not X = {1, 2, 3, 4}:
Neither E nor P covers the element 1.
On the other hand, there is no exact cover—indeed, not even a cover—of Y = {1, 2, 3, 4, 5} because
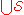= {1, 2, 3, 4} is a proper subset of Y:None of the subsets in
contains the element 5.Detailed example
Let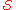 = {A, B, C, D, E, F} be a collection of subsetsof a set X = {1, 2, 3, 4, 5, 6, 7} such that:
- A = {1, 4, 7};
- B = {1, 4};
- C = {4, 5, 7};
- D = {3, 5, 6};
- E = {2, 3, 6, 7}; and
- F = {2, 7}.
Then the subcollection
= {B, D, F} is an exact cover, since each element in X is contained in exactly one of the subsets:
- B = {1, 4};
- D = {3, 5, 6}; or
- F = {2, 7}.
Moreover, {B, D, F} is the only exact cover, as the following argument demonstrates:
Because A and B are the only subsets containing 1, an exact cover must contain A or B, but not both.
If an exact cover contains A, then it doesn't contain B, C, E, or F, as each of these subsets has an element in common with A.
Then D is the only remaining subset, but the collection {A, D} doesn't cover the element 2.
In conclusion, there is no exact cover containing A.
On the other hand, if an exact cover contains B, then it doesn't contain A or C, as each of these subsets has an element in common with B.
Because D is the only remaining subset containing 5, D must be part of the exact cover.
If an exact cover contains D, then it doesn't contain E, as E has an element in common with D.
Then F is the only remaining subset, and the collection {B, D, F} is indeed an exact cover.
See the example in the article on Knuth's Algorithm X
Knuth's Algorithm X
Donald Knuth's Algorithm X is a recursive, nondeterministic, depth-first, backtracking algorithm that finds all solutions to the exact cover problem represented by a matrix A consisting of 0s and 1s...
for a matrix-based version of this argument.
Representations
An exact cover problem is defined by the binary relationBinary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
"contains" between subsets in
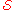and elements in X.There are different equivalent ways to represent this relation.
Standard representation
The standard way to represent the relation "contains" is to list the elements in each subset.For example, the detailed example above uses this standard representation:
- A = {1, 4, 7};
- B = {1, 4};
- C = {4, 5, 7};
- D = {3, 5, 6};
- E = {2, 3, 6, 7}; and
- F = {2, 7}.
Again, the subcollection
= {B, D, F} is an exact cover, since each element is contained in exactly one selected subset, as the highlighting makes clear.Inverse representation
The relation "contains" between subsets and elements can be invertedInverse relation
In mathematics, the inverse relation of a binary relation is the relation that occurs when you switch the order of the elements in the relation. For example, the inverse of the relation 'child of' is the relation 'parent of'...
, listing the subsets each element is contained in.
For example, the relation "contains" in the detailed example above can be represented by listing the subsets each element is contained in:
- 1 is contained in A, B;
- 2 is contained in E, F;
- 3 is contained in D, E;
- 4 is contained in A, B, C;
- 5 is contained in C, D;
- 6 is contained in D, E; and
- 7 is contained in A, C, E, F.
Again, the subcollection
= {B, D, F} is an exact cover, since each element is contained in exactly one selected subset, as the highlighting makes clear.When solving an exact cover problem, it is often useful to switch between the standard and inverse representations.
Matrix and hypergraph representations
The relation "contains" can be represented by an incidence matrixIncidence matrix
In mathematics, an incidence matrix is a matrix that shows the relationship between two classes of objects. If the first class is X and the second is Y, the matrix has one row for each element of X and one column for each element of Y. The entry in row x and column y is 1 if x and y are related ...
.
The matrix includes one row for each subset in
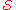and one column for each element in X.The entry in a particular row and column is 1 if the corresponding subset contains the corresponding element, and is 0 otherwise.
As each row represents the elements contained in the corresponding subset and each column represents the subsets containing the corresponding element, an incidence matrix effectively provides both the standard and inverse representations.
In the matrix representation, an exact cover is a selection of rows such that each column contains a 1 in exactly one selected row.
For example, the relation "contains" in the detailed example above can be represented by a 6×7 incidence matrix:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|
| A | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| B | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| C | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| D | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| E | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| F | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
Again, the subcollection
= {B, D, F} is an exact cover, since each element is contained in exactly one selected subset, i.e., each column contains a 1 in exactly one selected row, as the highlighting makes clear.See the example in the article on Knuth's Algorithm X
Knuth's Algorithm X
Donald Knuth's Algorithm X is a recursive, nondeterministic, depth-first, backtracking algorithm that finds all solutions to the exact cover problem represented by a matrix A consisting of 0s and 1s...
for a matrix-based solution to the detailed example above.
In turn, the incidence matrix can be seen also as describing a hypergraph
Hypergraph
In mathematics, a hypergraph is a generalization of a graph, where an edge can connect any number of vertices. Formally, a hypergraph H is a pair H = where X is a set of elements, called nodes or vertices, and E is a set of non-empty subsets of X called hyperedges or links...
. The hypergraph includes one node for each element in X and one edge for each subset in
; each node is included in exactly one of the edges forming the cover.Graph representation
The relation "contains" can be represented by a bipartite graphBipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
.
The vertices of the graph are divided into two disjoint sets, one representing the subsets in
and another representing the elements in X.If a subset contains an element, an edge connects the corresponding vertices in the graph.
In the graph representation, an exact cover is a selection of vertices corresponding to subsets such that each vertex corresponding to an element is connected to exactly one selected vertex.
For example, the relation "contains" in the detailed example above can be represented by a bipartite graph with 6+7 = 13 vertices:
= {B, D, F} is an exact cover, since each element is contained in exactly one selected subset, i.e., the vertex corresponding to each element in X is connected to exactly one selected vertex, as the highlighting makes clear.Equivalent problems
Although the canonical exact cover problem involves a collection of subsets of a set X, the logic does not depend on the presence of subsets containing elements.An "abstract exact cover problem" arises whenever there is a binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
between two sets P and Q and the goal is to select a subset P* of P such that each element in Q is related to exactly one element in P*.
In general, the elements of P represent choices and the elements of Q represent "exactly one" constraints on those choices.
More formally, given a binary relation R
P × Q between sets P and Q, one can call a subset P* of P an "abstract exact cover" of Q if each element in Q is R -1-related to exactly one element in P*.Here R -1 is the inverse
Inverse relation
In mathematics, the inverse relation of a binary relation is the relation that occurs when you switch the order of the elements in the relation. For example, the inverse of the relation 'child of' is the relation 'parent of'...
of R.
In general, R -1 restricted to Q × P* is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
from Q to P*, which maps each element in Q to the unique element in P* that is R-related that element in Q.
This function is onto, unless P* contains the "empty set," i.e., an element which isn't R-related to any element in Q.
In the canonical exact cover problem, P is a collection
of subsets of X, Q is the set X, R is the binary relation "contains" between subsets and elements, and R -1 restricted to Q × P* is the function "is contained in" from elements to selected subsets.Exact hitting set
In mathematicsMathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, given a collection
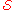of subsets of a set X, an exact hitting set X* is a subset of X such that each subset in 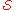contains exactly one element in X*. One says that each subset in 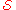is hit by exactly one element in X*.In computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, the exact hitting set problem is a decision problem
Decision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
to find an exact hitting set or else determine none exists.
The exact hitting set problem is an abstract exact cover problem.
In the notation above, P is the set X, Q is a collection
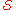of subsets of X, R is the binary relation "is contained in" between elements and subsets, and R -1 restricted to Q × P* is the function "contains" from subsets to selected elements.Whereas an exact cover problem involves selecting subsets and the relation "contains" from subsets to elements, an exact hitting set problem involves selecting elements and the relation "is contained in" from elements to subsets.
In a sense, an exact hitting set problem is the inverse of the exact cover problem involving the same set and collection of subsets.
Exact hitting set example
As in the detailed exact cover example above, let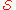 = {A, B, C, D, E, F} be a collection of subsets of a set X = {1, 2, 3, 4, 5, 6, 7} such that:
- A = {1, 4, 7};
- B = {1, 4};
- C = {4, 5, 7};
- D = {3, 5, 6};
- E = {2, 3, 6, 7}; and
- F = {2, 7}.
Then X* = {1, 2, 5} is an exact hitting set, since each subset in
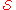contains exactly one element in X*, as the highlighting makes clear.Moreover, {1, 2, 5} is the only exact hitting set, as the following argument demonstrates:
Because 2 and 7 are the only elements that hit F, an exact hitting set must contain 2 or 7, but not both.
If an exact hitting set contains 7, then it doesn't contain 1, 2, 3, 4, 5, or 6, as each of these elements are contained in some subset also containing 7.
Then there are no more remaining elements, but {7} is not an exactly hitting set, as it doesn't hit B or D.
In conclusion, there is no exact hitting set containing 7.
On the other hand, if an exact hitting set contains 2, then it doesn't contain 3, 6, or 7, as each of these elements are contained in some subset also containing 2.
Because 5 is the only remaining element that hits D, the exact hitting set must contain 5.
If an exact hitting set contains 5, then it doesn't contain 4, as both hit C.
Because 1 is the only remaining element that hits A, the exact hitting set must contain 1.
Then there are no more remaining elements, and {1, 2, 5} is indeed an exact hitting set.
Although this example involves the same collection of subsets as the detailed exact cover example above, it is essentially a different problem. In a sense, the exact hitting set problem is the inverse (or transpose or converse) of the corresponding exact cover problem above, as the matrix representation makes clear:
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0 | 1 | 1 |
| 3 | 0 | 0 | 0 | 1 | 1 | 0 |
| 4 | 1 | 1 | 1 | 0 | 0 | 0 |
| 5 | 0 | 0 | 1 | 1 | 0 | 0 |
| 6 | 0 | 0 | 0 | 1 | 1 | 0 |
| 7 | 1 | 0 | 1 | 0 | 0 | 1 |
Dual example
But there is another exact hitting set problem that is essentially the same as the detailed exact cover example above, in which numbered elements become subsets and lettered subsets become elements, effectively inverting the relation between subsets and element.For example, as the subset B contains the elements 1 and 4 in the exact cover problem, the subsets I and IV contain the element b in the dual exact hitting set problem.
In particular, let
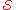= {I, II, III, IV, V, VI, VII} be a collection of subsets of a set X = {a, b, c, d, e, f} such that:
- I = {a, b}
- II = {e, f}
- III = {d, e}
- IV = {a, b, c}
- V = {c, d}
- VI = {d, e}
- VII = {a, c, e, f}
Then X* = {b, d, f} is an exact hitting set, since each subset in
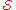contains (is hit by) exactly one element in X*, as the highlighting makes clear.The exact hitting set X* = {b, d, f} here is essentially the same as the exact cover
= {B, D, F} above, as the matrix representation makes clear:| I | II | III | IV | V | VI | VII | |
|---|---|---|---|---|---|---|---|
| a | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| b | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| c | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| d | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| e | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| f | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
Finding solutions
Knuth's Algorithm XKnuth's Algorithm X
Donald Knuth's Algorithm X is a recursive, nondeterministic, depth-first, backtracking algorithm that finds all solutions to the exact cover problem represented by a matrix A consisting of 0s and 1s...
is a recursive
Recursion (computer science)
Recursion in computer science is a method where the solution to a problem depends on solutions to smaller instances of the same problem. The approach can be applied to many types of problems, and is one of the central ideas of computer science....
, nondeterministic, depth-first, backtracking
Backtracking
Backtracking is a general algorithm for finding all solutions to some computational problem, that incrementally builds candidates to the solutions, and abandons each partial candidate c as soon as it determines that c cannot possibly be completed to a valid solution.The classic textbook example...
algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
that finds all solutions to the exact cover problem.
Dancing Links
Dancing Links
In computer science, Dancing Links, also known as DLX, is the technique suggested by Donald Knuth to efficiently implement his Algorithm X. Algorithm X is a recursive, nondeterministic, depth-first, backtracking algorithm that finds all solutions to the exact cover problem...
, commonly known as DLX, is the technique suggested by Donald Knuth
Donald Knuth
Donald Ervin Knuth is a computer scientist and Professor Emeritus at Stanford University.He is the author of the seminal multi-volume work The Art of Computer Programming. Knuth has been called the "father" of the analysis of algorithms...
to efficiently implement his Algorithm X on a computer.
Dancing Links uses the matrix representation of the problem.
Dancing Links implements the matrix as a series of doubly linked lists of the 1s of the matrix:
each 1 element has a link to the next 1 above, below, to the left, and to the right of itself.
Generalizations
In a standard exact cover problem, each constraint must be satisfied exactly once.It is a simple generalization to relax this requirement slightly and allow for the possibility that some "primary" constraints must be satisfied by exactly one selection but other "secondary" constraints can be satisfied by at most one selection.
As Knuth explains, a generalized exact cover problem can be converted to an equivalent exact cover problem by simply appending one row for each secondary column, containing a single 1 in that column. If in a particular candidate solution a particular secondary column is satisfied, then the added row isn't needed.
But if the secondary column isn't satisfied, as is allowed in the generalized problem but not the standard problem, then the added row can be selected to ensure the column is satisfied.
But Knuth goes on to explain that it is better working with the generalized problem directly, because the generalized algorithm is simpler and faster:
A simple change to his Algorithm X allows secondary columns to be handled directly.
The N queens problem is an example of a generalized exact cover problem, as the constraints corresponding to the diagonals of the chessboard need not be satisfied.
Noteworthy examples
Due to its NP-completeness, any problem in NP can be reducedReduction (complexity)
In computability theory and computational complexity theory, a reduction is a transformation of one problem into another problem. Depending on the transformation used this can be used to define complexity classes on a set of problems....
to exact cover problems, which then can be solved with techniques such as Dancing Links.
However, for some well known problems, the reduction is particularly direct.
For instance, the problem of tiling a board with pentominoes, and solving Sudoku
Sudoku
is a logic-based, combinatorial number-placement puzzle. The objective is to fill a 9×9 grid with digits so that each column, each row, and each of the nine 3×3 sub-grids that compose the grid contains all of the digits from 1 to 9...
can both be viewed as exact cover problems.
Pentomino tiling
The problem of tiling a 60-square board with 12 pentominoes is an example of an exact cover problem, as Donald KnuthDonald Knuth
Donald Ervin Knuth is a computer scientist and Professor Emeritus at Stanford University.He is the author of the seminal multi-volume work The Art of Computer Programming. Knuth has been called the "father" of the analysis of algorithms...
explains in his paper "Dancing links."
For example, consider the problem of tiling with pentominoes an 8×8 chessboard with the 4 central squares removed:
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 |
| 41 | 42 | 43 | 46 | 47 | 48 | ||
| 51 | 52 | 53 | 56 | 57 | 58 | ||
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 |
| 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 |
| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 |
The problem involves two kinds of constraints:
- Pentomino: For each of the 12 pentominoes, there is the constraint that it must be placed exactly once. Name these constraints after the corresponding pentominoes: F I L P N T U V W X Y Z.
- Square: For each of the 60 squares, there is the constraint that it must be covered by a pentomino exactly once. Name these constraints after the corresponding squares in the board: ij, where i is the rank and j is the file.
Thus there are 12+60 = 72 constraints in all.
As both kinds of constraints are "exactly one" constraints, the problem is an exact cover problem.
The problem involves many choices, one for each way to place a pentomino on the board.
It is convenient to consider each choice as a sets of 6 constraints: 1 constraint for the pentomino being placed and 5 constraints for the five squares where it is placed.
In the case of an 8×8 chessboard with the 4 central squares removed, there are 1568 such choices, for example:
- {F, 12, 13, 21, 22, 32}
- {F, 13, 14, 22, 23, 33}
- …
- {I, 11, 12, 13, 14, 15}
- {I, 12, 13, 14, 15, 16}
- …
- {L, 11, 21, 31, 41, 42}
- {L, 12, 22, 32, 42, 43}
- …
One of many solutions of this exact cover problem is the following set of 12 choices:
- {I, 11, 12, 13, 14, 15}
- {N, 16, 26, 27, 37, 47}
- {L, 17, 18, 28, 38, 48}
- {U, 21, 22, 31, 41, 42}
- {X, 23, 32, 33, 34, 43}
- {W, 24, 25, 35, 36, 46}
- {P, 51, 52, 53, 62, 63}
- {F, 56, 64, 65, 66, 75}
- {Z, 57, 58, 67, 76, 77}
- {T, 61, 71, 72, 73, 81}
- {V, 68, 78, 86, 87, 88}
- {Y, 74, 82, 83, 84, 85}
This set of choices corresponds to the following solution to the pentomino tiling problem:
Each choice is related to just 6 constraints, which are easy to enumerate. On the other hand, each constraint is related to many choices, which are harder to enumerate.
Whether viewed as an exact cover problem or an exact hitting set problem, the matrix representation is the same, having 1568 rows corresponding to choices and 72 columns corresponding to constraints.
Each row contains a single 1 in the column identifying the pentomino and five 1s in the columns identifying the squares covered by the pentomino.
Using the matrix, a computer can find all solutions relatively quickly, for example, using Dancing Links
Dancing Links
In computer science, Dancing Links, also known as DLX, is the technique suggested by Donald Knuth to efficiently implement his Algorithm X. Algorithm X is a recursive, nondeterministic, depth-first, backtracking algorithm that finds all solutions to the exact cover problem...
.
See also Solving Pentomino Puzzles with Backtracking.
Sudoku
The problem in SudokuSudoku
is a logic-based, combinatorial number-placement puzzle. The objective is to fill a 9×9 grid with digits so that each column, each row, and each of the nine 3×3 sub-grids that compose the grid contains all of the digits from 1 to 9...
is to assign numbers (or digits, values, symbols) to cells (or squares) in a grid so as to satisfy certain constraints.
In the standard 9×9 Sudoku variant, there are four kinds of constraints:
- Row-Column: Each intersection of a row and column, i.e, each cell, must contain exactly one number.
- Row-Number: Each row must contain each number exactly once
- Column-Number: Each column must contain each number exactly once.
- Box-Number: Each box must contain each number exactly once.
While the first constraint might seem trivial, it is nevertheless needed to ensure there is only one number per cell. Intuitively, placing a number into a cell prohibits placing that number in any other cell sharing the same column, row, or box and also prohibits placing any other number into the now occupied cell.
Solving Sudoku is an exact cover problem.
More precisely, solving Sudoku is an exact hitting set problem, which is equivalent to an exact cover problem (as in Example 5 above), when viewed as a problem to select possibilities such that each constraint set contains (i.e., is hit by) exactly one selected possibility.
In the notation above for the (generalized) exact cover problem, X is the set of possibilities, Y is a set of constraint sets, and R is the binary relation "is contained in."
Each possible assignment of a particular number to a particular cell is a possibility (or candidate).
When Sudoku is played with pencil and paper, possibilities are often called pencil marks.
In the standard 9×9 Sudoku variant, in which each of 9×9 cells is assigned one of 9 numbers, there are 9×9×9=729 possibilities.
Using obvious notation for rows, columns and numbers, the possibilities can be labeled
- R1C1#1, R1C1#2, …, R9C9#9.
The fact that each kind of constraint involves exactly one of something is what makes Sudoku an exact hitting set problem.
The constraints can be represented by constraint sets.
The problem is to select possibilities such that each constraint set contains (i.e., is hit by) exactly one selected possibility.
In the standard 9×9 Sudoku variant, there are four kinds of constraints sets corresponding to the four kinds of constraints:
- Row-Column: A row-column constraint set contains all the possibilities for the intersection of a particular row and column, i.e., for a cell. For example, the constraint set for row 1 and column 1, which can be labeled R1C1, contains the 9 possibilities for row 1 and column 1 but different numbers:
- R1C1 = { R1C1#1, R1C1#2, R1C1#3, R1C1#4, R1C1#5, R1C1#6, R1C1#7, R1C1#8, R1C1#9 }.
- Row-Number: A row-number constraint set contains all the possibilities for a particular row and number. For example, the constraint set for row 1 and number 1, which can be labeled R1#1, contains the 9 possibilities for row 1 and number 1 but different columns:
- R1#1 = { R1C1#1, R1C2#1, R1C3#1, R1C4#1, R1C5#1, R1C6#1, R1C7#1, R1C8#1, R1C9#1 }.
- Column-Number: A column-number constraint set contains all the possibilities for a particular column and number. For example, the constraint set for column 1 and number 1, which can be labeled C1#1, contains the 9 possibilities for column 1 and number 1 but different rows:
- C1#1 = { R1C1#1, R2C1#1, R3C1#1, R4C1#1, R5C1#1, R6C1#1, R7C1#1, R8C1#1, R9C1#1 }.
- Box-Number: A box-number constraint set contains all the possibilities for a particular box and number. For example, the constraint set for box 1 (in the upper lefthand corner) and number 1, which can be labeled B1#1, contains the 9 possibilities for the cells in box 1 and number 1:
- B1#1 = { R1C1#1, R1C2#1, R1C3#1, R2C1#1, R2C2#1, R2C3#1, R3C1#1, R3C2#1, R3C3#1 }.
Since there are 9 rows, 9 columns, 9 boxes and 9 numbers, there are 9×9=81 row-column constraint sets, 9×9=81 row-number constraint sets, 9×9=81 column-number constraint sets, and 9×9=81 box-number constraint sets: 81+81+81+81=324 constraint sets in all.
In brief, the standard 9×9 Sudoku variant is an exact hitting set problem with 729 possibilities and 324 constraint sets.
Thus the problem can be represented by a 729×324 matrix.
Although it is difficult to present the entire 729×324 matrix, the general nature of the matrix can be seen from several snapshots:
EWLINE
|
EWLINE
|
EWLINE
|
EWLINE
|
The complete 729×324 matrix is available from Bob Hanson.
Note that the set of possibilities RxCy#z can be arranged as a 9×9×9 cube in a 3-dimensional space with coordinates x, y, and z.
Then each row Rx, column Cy, or number #z is a 9×9×1 "slice" of possibilities; each box Bw is a 9x3×3 "tube" of possibilities; each row-column constraint set RxCy, row-number constraint set Rx#z, or column-number constraint set Cy#z is a 9x1×1 "strip" of possibilities; each box-number constraint set Bw#z is a 3x3×1 "square" of possibilities; and each possibility RxCy#z is a 1x1×1 "cubie" consisting of a single possibility.
Moreover, each constraint set or possibility is the intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of the component sets.
For example, R1C2#3 = R1 ∩ C2 ∩ #3, where ∩ denotes set intersection.
Although other Sudoku variations have different numbers of rows, columns, numbers and/or different kinds of constraints, they all involve possibilities and constraint sets, and thus can be seen as exact hitting set problems.
N queens problem
The N queens problem is an example of a generalized exact cover problem. The problem involves four kinds of constraints:
- Rank: For each of the N ranks, there must be exactly one queen.
- File: For each of the N files, there must be exactly one queen.
- Diagonals: For each of the 2N - 1 diagonals, there must be at most one queen.
- Reverse diagonals: For each of the 2N - 1 reverse diagonals, there must be at most one queen.
Note that the 2N rank and file constraints form the primary constraints, while the 4N - 2 diagonal and reverse diagonals form the secondary constraints. Further, because the each of first and last diagonal and reverse diagonals involve only one square on the chessboard, these can be omitted and thus we can reduce the number of secondary constraints to 4N - 6. The matrix for the N queens problem then have N2 rows and 6N - 6 columns, each row for a possible queen placement on each square on the chessboard, and each column for each constraint.
See also
- Constraint satisfaction problemConstraint satisfaction problemConstraint satisfaction problems s are mathematical problems defined as a set of objects whose state must satisfy a number of constraints or limitations. CSPs represent the entities in a problem as a homogeneous collection of finite constraints over variables, which is solved by constraint...
- Dancing LinksDancing LinksIn computer science, Dancing Links, also known as DLX, is the technique suggested by Donald Knuth to efficiently implement his Algorithm X. Algorithm X is a recursive, nondeterministic, depth-first, backtracking algorithm that finds all solutions to the exact cover problem...
- Difference map algorithmDifference map algorithmThe difference-map algorithm is a search algorithm for general constraint satisfaction problems. It is a meta-algorithm in the sense that it is built from more basic algorithms that perform projections onto constraint sets. From a mathematical perspective, the difference-map algorithm is a...
- Hitting set
- Karp's 21 NP-complete problemsKarp's 21 NP-complete problemsOne of the most important results in computational complexity theory was Stephen Cook's 1971 demonstration of the first NP-complete problem, the boolean satisfiability problem...
- Knuth's Algorithm XKnuth's Algorithm XDonald Knuth's Algorithm X is a recursive, nondeterministic, depth-first, backtracking algorithm that finds all solutions to the exact cover problem represented by a matrix A consisting of 0s and 1s...
- List of NP-complete problems
- Perfect matching and 3-dimensional matching3-dimensional matchingIn the mathematical discipline of graph theory, a 3-dimensional matching is a generalization of bipartite matching to 3-uniform hypergraphs...
are special cases of the exact cover problem
External links
- Implementation of an Exact Cover solver in C# - uses Algorithm X and Dancing Links.