Parallel postulate - AbsoluteAstronomy.com

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, the parallel postulate, also called Euclid
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...

's fifth postulate because it is the fifth postulate in Euclid's Elements

Euclid's Elements

Euclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...

, is a distinctive axiom

Axiom

In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...

in Euclidean geometry

Euclidean geometry

Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...

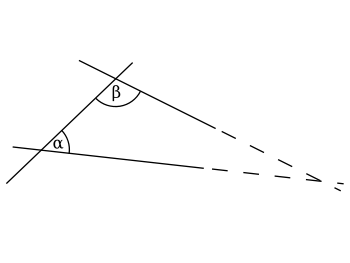
. It states that, in two dimensional geometry:

If a line segment
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...

intersects two straight lines
Line (mathematics)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...

forming two interior angles on the same side that sum to less than two right angle
Right angle
In geometry and trigonometry, a right angle is an angle that bisects the angle formed by two halves of a straight line. More precisely, if a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles...

s, then the two lines, if extended indefinitely, meet on that side on which the angles sum to less than two right angles.

Euclidean geometry is the study of geometry that satisfies all of Euclid's axioms, including the parallel postulate. A geometry where the parallel postulate does not hold is known as a non-Euclidean geometry

Non-Euclidean geometry

Non-Euclidean geometry is the term used to refer to two specific geometries which are, loosely speaking, obtained by negating the Euclidean parallel postulate, namely hyperbolic and elliptic geometry. This is one term which, for historical reasons, has a meaning in mathematics which is much...

. Geometry that is independent of Euclid's fifth postulate (i.e., only assumes the first four postulates) is known as absolute geometry

Absolute geometry

Absolute geometry is a geometry based on an axiom system for Euclidean geometry that does not assume the parallel postulate or any of its alternatives. The term was introduced by János Bolyai in 1832...

(or, in other places known as neutral geometry).

Converse of Euclid's parallel postulate

Euclid did not postulate the converse of his fifth postulate, which is one way to distinguish Euclidean geometry from elliptic geometry

Elliptic geometry

Elliptic geometry is a non-Euclidean geometry, in which, given a line L and a point p outside L, there exists no line parallel to L passing through p. Elliptic geometry, like hyperbolic geometry, violates Euclid's parallel postulate, which can be interpreted as asserting that there is exactly one...

. The Elements contains the proof of an equivalent statement (Book I, Proposition 27): If a straight line falling on two straight lines make the alternate angles equal to one another, the straight lines will be parallel to one another. As De Morgan

Augustus De Morgan

Augustus De Morgan was a British mathematician and logician. He formulated De Morgan's laws and introduced the term mathematical induction, making its idea rigorous. The crater De Morgan on the Moon is named after him....

pointed out, this is logically equivalent to (Book I, Proposition 16). These results do not depend upon the fifth postulate, but they do require the second postulate which is violated in elliptic geometry.

Logically equivalent properties

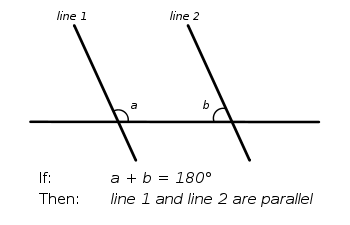
Probably the best known equivalent of Euclid's parallel postulate is Playfair's axiom

Playfair's axiom

Playfair's axiom is a geometrical axiom, intended to replace the fifth postulate of Euclides :Given a line and a point not on it, at most one parallel to the given line can be drawn through the point....

, named after the Scottish mathematician

Mathematician

A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....

John Playfair

John Playfair FRSE, FRS was a Scottish scientist and mathematician, and a professor of natural philosophy at the University of Edinburgh. He is perhaps best known for his book Illustrations of the Huttonian Theory of the Earth , which summarized the work of James Hutton...

, which states:

At most one line can be drawn through any point not on a given line parallel
Parallel (geometry)
Parallelism is a term in geometry and in everyday life that refers to a property in Euclidean space of two or more lines or planes, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid's parallel postulate. Two lines in a plane that do not...

to the given line in a plane.

Many other statements equivalent to the parallel postulate have been suggested, some of them appearing at first to be unrelated to parallelism, and some seeming so self-evident

Self-evidence

In epistemology , a self-evident proposition is one that is known to be true by understanding its meaning without proof....

that they were unconscious

Unconscious mind

The unconscious mind is a term coined by the 18th century German romantic philosopher Friedrich Schelling and later introduced into English by the poet and essayist Samuel Taylor Coleridge...

ly assumed by people who claimed to have proven the parallel postulate from Euclid's other postulates. This is a summary

There is at most one line that can be drawn parallel to another given one by an external point. (Playfair's axiom
Playfair's axiom
Playfair's axiom is a geometrical axiom, intended to replace the fifth postulate of Euclides :Given a line and a point not on it, at most one parallel to the given line can be drawn through the point....

)
The sum of the angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...

s in every triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....

is 180° (triangle postulate
Triangle postulate
In Euclidean geometry, the triangle postulate states that the sum of the angles of a triangle is two right angles. This postulate is equivalent to the parallel postulate...

).
There exists a triangle whose angles add up to 180°.
The sum of the angles is the same for every triangle.
There exists a pair of similar
Similarity (geometry)
Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...

, but not congruent
Congruence (geometry)
In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...

, triangles.
Every triangle can be circumscribed.
If three angles of a quadrilateral
Quadrilateral
In Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...

are right angle
Right angle
In geometry and trigonometry, a right angle is an angle that bisects the angle formed by two halves of a straight line. More precisely, if a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles...

s, then the fourth angle is also a right angle.
There exists a quadrilateral of which all angles are right angles.
There exists a pair of straight lines that are at constant distance
Distance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...

from each other.
Two lines that are parallel to the same line are also parallel to each other.
In a right-angled triangle, the square of the hypotenuse equals the sum of the squares of the other two sides (Pythagoras' Theorem).
There is no upper limit to the area of a triangle. (Wallis axiom)
The summit angles of the Saccheri quadrilateral
Saccheri quadrilateral
A Saccheri quadrilateral is a quadrilateral with two equal sides perpendicular to the base. It is named after Giovanni Gerolamo Saccheri, who used it extensively in his book Euclid vindicatus , an attempt to prove the parallel postulate using the method Reductio ad absurdum...

are 90°.
If a line intersects one of two parallel lines, both of which are coplanar with the original line, then it also intersects the other. (Proclus
Proclus
Proclus Lycaeus , called "The Successor" or "Diadochos" , was a Greek Neoplatonist philosopher, one of the last major Classical philosophers . He set forth one of the most elaborate and fully developed systems of Neoplatonism...

' axiom)

However, the alternatives which employ the word "parallel" cease appearing so simple when one is obliged to explain which of the three common definitions of "parallel" is meant - constant separation, never meeting, or same angles where crossed by a third line - since the equivalence of these three is itself one of the unconsciously obvious assumptions equivalent to Euclid's fifth postulate. For example, if the word "parallel" in Playfair's axiom is taken to mean 'constant separation', then it is no longer equivalent to Euclid's fifth postulate, and is provable from the first four (the axiom says 'There is at most one line…', which is consistent with there being no such lines). However, if the definition is taken so that parallel lines are lines that do not intersect, Playfair's axiom is equivalent to Euclid's fifth postulate and is thus independent of the first four postulates.

History

For two thousand years, many attempts were made to prove the parallel postulate using Euclid's first four postulates. The main reason that such a proof was so highly sought after was that, unlike the first four postulates, the parallel postulate isn't self-evident. If the order the postulates were listed in the Elements is significant, it indicates that Euclid included this postulate only when he realised he could not prove it or proceed without it.
Many attempts were made to prove the fifth postulate from the other four, many of them being accepted as proofs for long periods of time until the mistake was found. Invariably the mistake was assuming some 'obvious' property which turned out to be equivalent to the fifth postulate (Playfair's axiom). Although known from the time of Proclus, this became known as Playfair's Axiom after John Playfair wrote a famous commentary on Euclid in 1795 in which he proposed replacing Euclid's fifth postulate by his own axiom.

Proclus

Proclus

Proclus Lycaeus , called "The Successor" or "Diadochos" , was a Greek Neoplatonist philosopher, one of the last major Classical philosophers . He set forth one of the most elaborate and fully developed systems of Neoplatonism...

(410-485) wrote a commentary on The Elements
Euclid's Elements
Euclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...

where he comments on attempted proofs to deduce the fifth postulate from the other four, in particular he notes that Ptolemy

Ptolemy

Claudius Ptolemy , was a Roman citizen of Egypt who wrote in Greek. He was a mathematician, astronomer, geographer, astrologer, and poet of a single epigram in the Greek Anthology. He lived in Egypt under Roman rule, and is believed to have been born in the town of Ptolemais Hermiou in the...

had produced a false 'proof'. Proclus then goes on to give a false proof of his own. However he did give a postulate which is equivalent to the fifth postulate.

Ibn al-Haytham (Alhazen) (965-1039), an Iraqi mathematician, made the first attempt at proving the parallel postulate using a proof by contradiction

Reductio ad absurdum

In logic, proof by contradiction is a form of proof that establishes the truth or validity of a proposition by showing that the proposition's being false would imply a contradiction...

, where he introduced the concept of motion

Hyperbolic motion

In geometry, hyperbolic motions are isometric automorphisms of a hyperbolic space. Under composition of mappings, the hyperbolic motions form a continuous group. This group is said to characterize the hyperbolic space. Such an approach to geometry was cultivated by Felix Klein in his Erlangen program...

and transformation into geometry. He formulated the Lambert quadrilateral

Lambert quadrilateral

In geometry, a Lambert quadrilateral,named after Johann Heinrich Lambert,is a quadrilateral three of whose angles are right angles. Historically, the fourth angle of a Lambert quadrilateral was of considerable interest since if it could be shown to be a right angle, then the Euclidean parallel...

, which Boris Abramovich Rozenfeld names the "Ibn al-Haytham–Lambert quadrilateral", and his attempted proof also shows similarities to Playfair's axiom.

Omar Khayyám

Omar Khayyám

Omar Khayyám was aPersian polymath: philosopher, mathematician, astronomer and poet. He also wrote treatises on mechanics, geography, mineralogy, music, climatology and theology....

(1050–1123), a Persian, made the first attempt at formulating a non-Euclidean postulate as an alternative to the parallel postulate, and he was the first to consider the cases of elliptical geometry and hyperbolic geometry

Hyperbolic geometry

In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...

, though he excluded the latter. The Khayyam-Saccheri quadrilateral

Saccheri quadrilateral

A Saccheri quadrilateral is a quadrilateral with two equal sides perpendicular to the base. It is named after Giovanni Gerolamo Saccheri, who used it extensively in his book Euclid vindicatus , an attempt to prove the parallel postulate using the method Reductio ad absurdum...

was also first considered by Omar Khayyam in the late 11th century in Book I of Explanations of the Difficulties in the Postulates of Euclid. Unlike many commentators on Euclid before and after him (including Giovanni Girolamo Saccheri

Giovanni Girolamo Saccheri

Giovanni Girolamo Saccheri was an Italian Jesuit priest, scholastic philosopher, and mathematician....

), Khayyam was not trying to prove the parallel postulate as such but to derive it from an equivalent postulate: "Two convergent straight lines intersect and it is impossible for two convergent straight lines to diverge in the direction in which they converge." He recognized that three possibilities arose from omitting Euclid's Fifth; if two perpendiculars to one line cross another line, judicious choice of the last can make the internal angles where it meets the two perpendiculars equal (it is then parallel to the first line). If those equal internal angles are right angles, we get Euclid's Fifth; otherwise, they must be either acute or obtuse. He persuaded himself that the acute and obtuse cases lead to contradiction, but had made a tacit assumption equivalent to the fifth to get there.

Nasir al-Din al-Tusi

Nasir al-Din al-Tusi

Khawaja Muḥammad ibn Muḥammad ibn Ḥasan Ṭūsī , better known as Naṣīr al-Dīn al-Ṭūsī , was a Persian polymath and prolific writer: an astronomer, biologist, chemist, mathematician, philosopher, physician, physicist, scientist, theologian and Marja Taqleed...

(1201–1274), in his Al-risala al-shafiya'an al-shakk fi'l-khutut al-mutawaziya (Discussion Which Removes Doubt about Parallel Lines) (1250), wrote detailed critiques of the parallel postulate and on Khayyám's attempted proof a century earlier. Nasir al-Din attempted to derive a proof by contradiction of the parallel postulate. He was also one of the first to consider the cases of elliptical geometry and hyperbolic geometry, though he ruled out both of them.

Nasir al-Din's son, Sadr al-Din (sometimes known as "Pseudo-Tusi"), wrote a book on the subject in 1298, based on his father's later thoughts, which presented one of the earliest arguments for a non-Euclidean hypothesis equivalent to the parallel postulate. "He essentially revised both the Euclidean system of axioms and postulates and the proofs of many propositions from the Elements." His work was published in Rome

Rome

Rome is the capital of Italy and the country's largest and most populated city and comune, with over 2.7 million residents in . The city is located in the central-western portion of the Italian Peninsula, on the Tiber River within the Lazio region of Italy.Rome's history spans two and a half...

in 1594 and was studied by European geometers. This work marked the starting point for Saccheri's work on the subject wherein he criticised this work as well as the work of Wallis.
Giordano Vitale (1633-1711), in his book Euclide restituo (1680, 1686), used the Khayyam-Saccheri quadrilateral to prove that if three points are equidistant on the base AB and the summit CD, then AB and CD are everywhere equidistant. Girolamo Saccheri (1667-1733) pursued the same line of reasoning more thoroughly, correctly obtaining absurdity from the obtuse case (proceeding, like Euclid, from the implicit assumption that lines can be extended indefinitely and have infinite length), but failing to debunk the acute case (although he managed to wrongly persuade himself that he had).

Where Khayyám and Saccheri had attempted to prove Euclid's fifth by disproving the only possible alternatives, the nineteenth century finally saw mathematicians exploring those alternatives and discovering the logically consistent geometries which result. In 1829, Nikolai Ivanovich Lobachevsky

Nikolai Ivanovich Lobachevsky

Nikolai Ivanovich Lobachevsky was a Russian mathematician and geometer, renowned primarily for his pioneering works on hyperbolic geometry, otherwise known as Lobachevskian geometry...

published an account of acute geometry in an obscure Russian journal (later re-published in 1840 in German). In 1831, János Bolyai

János Bolyai

János Bolyai was a Hungarian mathematician, known for his work in non-Euclidean geometry.Bolyai was born in the Transylvanian town of Kolozsvár , then part of the Habsburg Empire , the son of Zsuzsanna Benkő and the well-known mathematician Farkas Bolyai.-Life:By the age of 13, he had mastered...

included, in a book by his father, an appendix describing acute geometry, which, doubtlessly, he had developed independently of Lobachevsky. Carl Friedrich Gauss

Carl Friedrich Gauss

Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...

had also studied the problem, but he did not publish any of his results. Upon hearing of Bolyai's results in a letter from Bolyai's father, Farkas Bolyai

Farkas Bolyai

Farkas Bolyai was a Hungarian mathematician, mainly known for his work in geometry, and of his son János Bolyai.-Biography:...

, he stated:

"If I commenced by saying that I am unable to praise this work, you would certainly be surprised for a moment. But I cannot say otherwise. To praise it would be to praise myself. Indeed the whole contents of the work, the path taken by your son, the results to which he is led, coincide almost entirely with my meditations, which have occupied my mind partly for the last thirty or thirty-five years."

The resulting geometries were later developed by Lobachevsky

Nikolai Ivanovich Lobachevsky

Nikolai Ivanovich Lobachevsky was a Russian mathematician and geometer, renowned primarily for his pioneering works on hyperbolic geometry, otherwise known as Lobachevskian geometry...

, Riemann

Bernhard Riemann

Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....

and Poincaré into hyperbolic geometry

Hyperbolic geometry

In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...

(the acute case) and spherical geometry

Spherical geometry

Spherical geometry is the geometry of the two-dimensional surface of a sphere. It is an example of a geometry which is not Euclidean. Two practical applications of the principles of spherical geometry are to navigation and astronomy....

(the obtuse case). The independence

Independence (mathematical logic)

In mathematical logic, independence refers to the unprovability of a sentence from other sentences.A sentence σ is independent of a given first-order theory T if T neither proves nor refutes σ; that is, it is impossible to prove σ from T, and it is also impossible to prove from T that...

of the parallel postulate from Euclid's other axioms was finally demonstrated by Eugenio Beltrami

Eugenio Beltrami

Eugenio Beltrami was an Italian mathematician notable for his work concerning differential geometry and mathematical physics...

in 1868.

Criticism

Attempts to logically prove this postulate, rather than the eighth axiom, were criticized by Schopenhauer, as described in Schopenhauer's criticism of the proofs of the Parallel Postulate

Schopenhauer's criticism of the proofs of the parallel postulate

Arthur Schopenhauer criticized mathematicians' attempts to prove Euclid's Parallel Postulate because they try to prove from indirect concepts that which is directly evident from perception....

. However, the argument used by Schopenhauer was that the postulate is evident by perception, not that it was not a logical consequence of the other axioms.

Converse of Euclid's parallel postulate

Logically equivalent properties

History

Criticism

See also

Further reading