
Distribution (differential geometry)
Encyclopedia
In differential geometry, a discipline within mathematics
, a distribution is a subset of the tangent bundle
of a manifold
satisfying certain properties. Distributions are used to build up notions of integrability
, and specifically of a foliation
of a manifold.
Even though they share the same name, distributions we discuss in this article have nothing to do with distribution
s in the sense of analysis.
 be a
be a 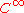 manifold of dimension
manifold of dimension  , and let
, and let  . Suppose that for each
. Suppose that for each  , we assign an
, we assign an  -dimensional subspace
-dimensional subspace
 of the tangent space
of the tangent space
in such a way that for a neighbourhood
 of
of  there exist
there exist  linearly independent
linearly independent
smooth vector field
s such that for any point
such that for any point 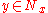 ,
,  span
span
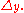 We let
We let  refer to the collection of all the
refer to the collection of all the  for all
for all  and we then call
and we then call  a distribution of dimension
a distribution of dimension  on
on  , or sometimes a
, or sometimes a 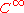
 -plane distribution on
-plane distribution on 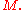 The set of smooth vector fields
The set of smooth vector fields  is called a local basis of
is called a local basis of 
 on
on  is involutive if for every point
is involutive if for every point  there exists a local basis
there exists a local basis  of the distribution in a neighbourhood of
of the distribution in a neighbourhood of  such that for all
such that for all 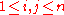 ,
, 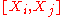 (the Lie bracket
(the Lie bracket
of two vector fields) is in the span of That is, if
That is, if 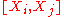 is a linear combination
is a linear combination
of Normally this is written as
Normally this is written as 
Involutive distributions are the tangent spaces to foliation
s. Involutive distributions are important in that they satisfy the conditions of the Frobenius theorem
, and thus lead to integrable system
s.
A related idea occurs in Hamiltonian mechanics
: two functions f and g on a symplectic manifold
are said to be in mutual involution if their Poisson bracket
vanishes.
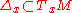 are not required to all be of the same dimension. The definition requires that the
are not required to all be of the same dimension. The definition requires that the  are determined locally by a set of vector fields, but these will no longer be linearly independent everywhere. It is not hard to see that the dimension of
are determined locally by a set of vector fields, but these will no longer be linearly independent everywhere. It is not hard to see that the dimension of 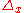 is lower semicontinuous, so that at special points the dimension is lower than at nearby points.
is lower semicontinuous, so that at special points the dimension is lower than at nearby points.
One class of examples is furnished by a non-free action of a Lie group
on a manifold, the vector fields in question being the infinitesimal generators of the group action
(a free action gives rise to a genuine distribution). Another arises in dynamical systems, where the set of vector fields in the definition is the set of vector fields that commute with a given one. There are also examples and applications in Control theory
, where the generalized distribution represents infinitesimal constraints of the system.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a distribution is a subset of the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
of a manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
satisfying certain properties. Distributions are used to build up notions of integrability
Integrable system
In mathematics and physics, there are various distinct notions that are referred to under the name of integrable systems.In the general theory of differential systems, there is Frobenius integrability, which refers to overdetermined systems. In the classical theory of Hamiltonian dynamical...
, and specifically of a foliation
Foliation
In mathematics, a foliation is a geometric device used to study manifolds, consisting of an integrable subbundle of the tangent bundle. A foliation looks locally like a decomposition of the manifold as a union of parallel submanifolds of smaller dimension....
of a manifold.
Even though they share the same name, distributions we discuss in this article have nothing to do with distribution
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
s in the sense of analysis.
Definition
Let be a
be a 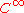 manifold of dimension
manifold of dimension  , and let
, and let  . Suppose that for each
. Suppose that for each  , we assign an
, we assign an  -dimensional subspace
-dimensional subspaceLinear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
 of the tangent space
of the tangent spaceTangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
in such a way that for a neighbourhood
Neighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
 of
of  there exist
there exist  linearly independent
linearly independentLinear independence
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
smooth vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s
 such that for any point
such that for any point 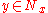 ,
,  span
spanLinear span
In the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set...
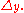 We let
We let  refer to the collection of all the
refer to the collection of all the  for all
for all  and we then call
and we then call  a distribution of dimension
a distribution of dimension  on
on  , or sometimes a
, or sometimes a 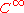
 -plane distribution on
-plane distribution on 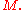 The set of smooth vector fields
The set of smooth vector fields  is called a local basis of
is called a local basis of 
Involutive distributions
We say that a distribution on
on  is involutive if for every point
is involutive if for every point  there exists a local basis
there exists a local basis  of the distribution in a neighbourhood of
of the distribution in a neighbourhood of  such that for all
such that for all 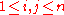 ,
, 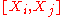 (the Lie bracket
(the Lie bracketLie bracket of vector fields
In the mathematical field of differential topology, the Lie bracket of vector fields, Jacobi–Lie bracket, or commutator of vector fields is a bilinear differential operator which assigns, to any two vector fields X and Y on a smooth manifold M, a third vector field denoted [X, Y]...
of two vector fields) is in the span of
 That is, if
That is, if 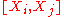 is a linear combination
is a linear combinationLinear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of
 Normally this is written as
Normally this is written as 
Involutive distributions are the tangent spaces to foliation
Foliation
In mathematics, a foliation is a geometric device used to study manifolds, consisting of an integrable subbundle of the tangent bundle. A foliation looks locally like a decomposition of the manifold as a union of parallel submanifolds of smaller dimension....
s. Involutive distributions are important in that they satisfy the conditions of the Frobenius theorem
Frobenius theorem (differential topology)
In mathematics, Frobenius' theorem gives necessary and sufficient conditions for finding a maximal set of independent solutions of an overdetermined system of first-order homogeneous linear partial differential equations...
, and thus lead to integrable system
Integrable system
In mathematics and physics, there are various distinct notions that are referred to under the name of integrable systems.In the general theory of differential systems, there is Frobenius integrability, which refers to overdetermined systems. In the classical theory of Hamiltonian dynamical...
s.
A related idea occurs in Hamiltonian mechanics
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
: two functions f and g on a symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
are said to be in mutual involution if their Poisson bracket
Poisson bracket
In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system...
vanishes.
Generalized distributions
A generalized distribution, or Stefan-Sussmann distribution, is similar to a distribution, but the subspaces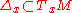 are not required to all be of the same dimension. The definition requires that the
are not required to all be of the same dimension. The definition requires that the  are determined locally by a set of vector fields, but these will no longer be linearly independent everywhere. It is not hard to see that the dimension of
are determined locally by a set of vector fields, but these will no longer be linearly independent everywhere. It is not hard to see that the dimension of 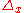 is lower semicontinuous, so that at special points the dimension is lower than at nearby points.
is lower semicontinuous, so that at special points the dimension is lower than at nearby points.One class of examples is furnished by a non-free action of a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
on a manifold, the vector fields in question being the infinitesimal generators of the group action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
(a free action gives rise to a genuine distribution). Another arises in dynamical systems, where the set of vector fields in the definition is the set of vector fields that commute with a given one. There are also examples and applications in Control theory
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
, where the generalized distribution represents infinitesimal constraints of the system.

