
Foliation
Encyclopedia
In mathematics
, a foliation is a geometric device used to study manifolds, consisting of an integrable subbundle of the tangent bundle
. A foliation looks locally like a decomposition of the manifold as a union of parallel submanifolds of smaller dimension.
 foliation
foliation 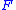 of an
of an  -dimensional manifold
-dimensional manifold
 is a covering by charts
is a covering by charts 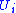 together with maps
together with maps
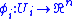
such that on the overlaps the transition function
the transition function
s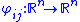 defined by
defined by
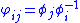
take the form

where denotes the first
denotes the first  coordinates, and
coordinates, and  denotes the last p co-ordinates. That is,
denotes the last p co-ordinates. That is,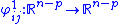
and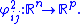
In the chart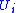 , the stripes
, the stripes  constant
constant
match up with the stripes on other charts . Technically, these stripes are called plaques of the foliation. In each chart, the plaques are
. Technically, these stripes are called plaques of the foliation. In each chart, the plaques are  dimensional submanifold
dimensional submanifold
s. These submanifolds piece together from chart to chart to form maximal connected
injectively immersed submanifolds called the leaves of the foliation.
The notion of leaves allows for a more intuitive way of thinking about a foliation. A -dimensional foliation of a
-dimensional foliation of a  -manifold
-manifold  may be thought of as simply a collection
may be thought of as simply a collection 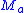 of pairwise-disjoint, connected
of pairwise-disjoint, connected  -dimensional sub-manifolds (the leaves of the foliation) of
-dimensional sub-manifolds (the leaves of the foliation) of  , such that for every point
, such that for every point  in
in  , there is a chart
, there is a chart 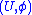 with
with  homeomorphic to
homeomorphic to 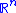 containing
containing  such that for every leaf
such that for every leaf 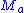 ,
, 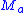 meets
meets  in either the empty set or a countable collection of subspaces whose images in
in either the empty set or a countable collection of subspaces whose images in 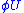 are
are  -dimensional affine subspaces whose first
-dimensional affine subspaces whose first  coordinates are constant.
coordinates are constant.
If we shrink the chart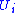 it can be written in the form
it can be written in the form 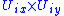 where
where and
and  and
and 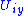
is isomorphic to the plaques and the points of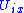 parametrize the plaques in
parametrize the plaques in 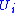 . If we pick a
. If we pick a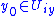 ,
, 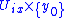
is a submanifold of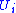 that intersects every plaque exactly once. This is called a local transversal section
that intersects every plaque exactly once. This is called a local transversal section
of the foliation. Note that due to monodromy there might not exist global transversal sections of the foliation.
 -dimensional space, foliated as a product by subspaces consisting of points whose first
-dimensional space, foliated as a product by subspaces consisting of points whose first  co-ordinates are constant. This can be covered with a single chart. The statement is essentially that
co-ordinates are constant. This can be covered with a single chart. The statement is essentially that
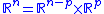
with the leaves or plaques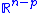 being enumerated by
being enumerated by 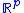 . The analogy is seen directly in three dimensions, by taking
. The analogy is seen directly in three dimensions, by taking  and
and  : the two-dimensional leaves of a book are enumerated by a (one-dimensional) page number.
: the two-dimensional leaves of a book are enumerated by a (one-dimensional) page number.
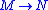 is a covering between manifolds, and
is a covering between manifolds, and 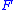 is a foliation on
is a foliation on  , then it pulls back to a foliation on
, then it pulls back to a foliation on  . More generally, if the map is merely a branched covering, where the branch locus
. More generally, if the map is merely a branched covering, where the branch locus
is transverse to the foliation, then the foliation can be pulled back.
 (where
(where  ) is a submersion
) is a submersion
of manifolds, it follows from the inverse function theorem
that the connected components of the fibers of the submersion define a codimension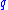 foliation of
foliation of  . Fiber bundles are an example of this type.
. Fiber bundles are an example of this type.
 is a Lie group
is a Lie group
, and is a subgroup
is a subgroup
obtained by exponentiating a closed subalgebra
of the Lie algebra
of , then
, then  is foliated by coset
is foliated by coset
s of .
.
 be a Lie group acting smoothly on a manifold
be a Lie group acting smoothly on a manifold  . If the action is a locally free action or free action, then the orbits of
. If the action is a locally free action or free action, then the orbits of  define a foliation of
define a foliation of  .
.
T = R2/Z2 with the same slope θ forms a foliation. The leaves are obtained by projecting straight lines of slope θ in the plane R2 onto the torus. If the slope is rational
then all leaves are closed curves homeomorphic to the circle
, while if it is irrational
, the leaves are noncompact, homeomorphic to the real line
, and dense
in the torus (cf Irrational rotation
). The irrational case is known as the Kronecker foliation, after Leopold Kronecker
. A similar construction using a foliation of Rn by parallel lines yields a one-dimensional foliation of the n-torus Rn/Zn associated with the linear flow on the torus.
, with vector field
s: given a vector field
on that is never zero, its integral curve
that is never zero, its integral curve
s will give a 1-dimensional foliation. (i.e. a codimension foliation).
foliation).
This observation generalises to the Frobenius theorem
, saying that the necessary and sufficient conditions
for a distribution (i.e. an dimensional subbundle
dimensional subbundle
of the tangent bundle
of a manifold) to be tangent to the leaves of a foliation, is that the set of vector fields tangent to the distribution are closed under Lie bracket
. One can also phrase this differently, as a question of reduction of the structure group
of the tangent bundle
from to a reducible subgroup.
to a reducible subgroup.
The conditions in the Frobenius theorem appear as integrability conditions; and the assertion is that if those are fulfilled the reduction can take place because local transition functions with the required block structure
exist. For example, in the codimension 1 case, we can define the tangent bundle of the foliation as , for some (non-canonical)
, for some (non-canonical)  (ie a non-zero co-vector field). A given
(ie a non-zero co-vector field). A given  is integrable iff
is integrable iff  everywhere.
everywhere.
There is a global foliation theory, because topological constraints exist. For example in the surface
case, an everywhere non-zero vector field can exist on an orientable compact
surface only for the torus
. This is a consequence of the Poincaré–Hopf index theorem, which shows the Euler characteristic
will have to be 0. There are many deep connections with contact topology, which is the "opposite" concept.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a foliation is a geometric device used to study manifolds, consisting of an integrable subbundle of the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
. A foliation looks locally like a decomposition of the manifold as a union of parallel submanifolds of smaller dimension.
Definition
More formally, a dimensionDimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
 foliation
foliation 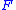 of an
of an  -dimensional manifold
-dimensional manifold is a covering by charts
is a covering by charts 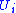 together with maps
together with maps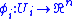
such that on the overlaps
 the transition function
the transition functionTransition function
In mathematics, a transition function has several different meanings:* In topology, a transition function is a homeomorphism from one coordinate chart to another...
s
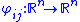 defined by
defined by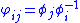
take the form

where
 denotes the first
denotes the first  coordinates, and
coordinates, and  denotes the last p co-ordinates. That is,
denotes the last p co-ordinates. That is,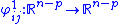
and
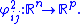
In the chart
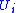 , the stripes
, the stripes  constant
constantMathematical constant
A mathematical constant is a special number, usually a real number, that is "significantly interesting in some way". Constants arise in many different areas of mathematics, with constants such as and occurring in such diverse contexts as geometry, number theory and calculus.What it means for a...
match up with the stripes on other charts
 . Technically, these stripes are called plaques of the foliation. In each chart, the plaques are
. Technically, these stripes are called plaques of the foliation. In each chart, the plaques are  dimensional submanifold
dimensional submanifoldSubmanifold
In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
s. These submanifolds piece together from chart to chart to form maximal connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
injectively immersed submanifolds called the leaves of the foliation.
The notion of leaves allows for a more intuitive way of thinking about a foliation. A
 -dimensional foliation of a
-dimensional foliation of a  -manifold
-manifold  may be thought of as simply a collection
may be thought of as simply a collection 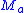 of pairwise-disjoint, connected
of pairwise-disjoint, connected  -dimensional sub-manifolds (the leaves of the foliation) of
-dimensional sub-manifolds (the leaves of the foliation) of  , such that for every point
, such that for every point  in
in  , there is a chart
, there is a chart 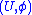 with
with  homeomorphic to
homeomorphic to 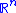 containing
containing  such that for every leaf
such that for every leaf 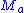 ,
, 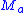 meets
meets  in either the empty set or a countable collection of subspaces whose images in
in either the empty set or a countable collection of subspaces whose images in 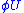 are
are  -dimensional affine subspaces whose first
-dimensional affine subspaces whose first  coordinates are constant.
coordinates are constant.If we shrink the chart
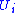 it can be written in the form
it can be written in the form 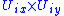 where
where and
and  and
and 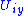
is isomorphic to the plaques and the points of
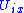 parametrize the plaques in
parametrize the plaques in 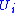 . If we pick a
. If we pick a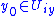 ,
, 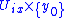
is a submanifold of
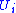 that intersects every plaque exactly once. This is called a local transversal section
that intersects every plaque exactly once. This is called a local transversal sectionSection (category theory)
In category theory, a branch of mathematics, a section is a right inverse of a morphism. Dually, a retraction is a left inverse...
of the foliation. Note that due to monodromy there might not exist global transversal sections of the foliation.
Flat space
Consider an -dimensional space, foliated as a product by subspaces consisting of points whose first
-dimensional space, foliated as a product by subspaces consisting of points whose first  co-ordinates are constant. This can be covered with a single chart. The statement is essentially that
co-ordinates are constant. This can be covered with a single chart. The statement is essentially that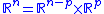
with the leaves or plaques
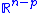 being enumerated by
being enumerated by 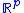 . The analogy is seen directly in three dimensions, by taking
. The analogy is seen directly in three dimensions, by taking  and
and  : the two-dimensional leaves of a book are enumerated by a (one-dimensional) page number.
: the two-dimensional leaves of a book are enumerated by a (one-dimensional) page number.Covers
If is a covering between manifolds, and
is a covering between manifolds, and 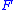 is a foliation on
is a foliation on  , then it pulls back to a foliation on
, then it pulls back to a foliation on  . More generally, if the map is merely a branched covering, where the branch locus
. More generally, if the map is merely a branched covering, where the branch locusLocus (mathematics)
In geometry, a locus is a collection of points which share a property. For example a circle may be defined as the locus of points in a plane at a fixed distance from a given point....
is transverse to the foliation, then the foliation can be pulled back.
Submersions
If (where
(where  ) is a submersion
) is a submersionSubmersion (mathematics)
In mathematics, a submersion is a differentiable map between differentiable manifolds whose differential is everywhere surjective. This is a basic concept in differential topology...
of manifolds, it follows from the inverse function theorem
Inverse function theorem
In mathematics, specifically differential calculus, the inverse function theorem gives sufficient conditions for a function to be invertible in a neighborhood of a point in its domain...
that the connected components of the fibers of the submersion define a codimension
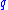 foliation of
foliation of  . Fiber bundles are an example of this type.
. Fiber bundles are an example of this type.Lie groups
If is a Lie group
is a Lie groupLie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
, and
 is a subgroup
is a subgroupSubgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
obtained by exponentiating a closed subalgebra
Subalgebra
In mathematics, the word "algebra", when referring to a structure, often means a vector space or module equipped with an additional bilinear operation. Algebras in universal algebra are far more general: they are a common generalisation of all algebraic structures...
of the Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of
 , then
, then  is foliated by coset
is foliated by cosetCoset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
s of
 .
.Lie group actions
Let be a Lie group acting smoothly on a manifold
be a Lie group acting smoothly on a manifold  . If the action is a locally free action or free action, then the orbits of
. If the action is a locally free action or free action, then the orbits of  define a foliation of
define a foliation of  .
.Kronecker foliation
The set of lines on the torusTorus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
T = R2/Z2 with the same slope θ forms a foliation. The leaves are obtained by projecting straight lines of slope θ in the plane R2 onto the torus. If the slope is rational
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
then all leaves are closed curves homeomorphic to the circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
, while if it is irrational
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
, the leaves are noncompact, homeomorphic to the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
, and dense
Dense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
in the torus (cf Irrational rotation
Irrational rotation
In mathematical theory of dynamical systems, an irrational rotation is a mapwhere θ is an irrational number. Under the identification of a circle with R/Z, or with the interval [0, 1] with the boundary points glued together, this map becomes a rotation of a circle by a proportion θ of a full...
). The irrational case is known as the Kronecker foliation, after Leopold Kronecker
Leopold Kronecker
Leopold Kronecker was a German mathematician who worked on number theory and algebra.He criticized Cantor's work on set theory, and was quoted by as having said, "God made integers; all else is the work of man"...
. A similar construction using a foliation of Rn by parallel lines yields a one-dimensional foliation of the n-torus Rn/Zn associated with the linear flow on the torus.
Foliations and integrability
There is a close relationship, assuming everything is smoothSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
, with vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s: given a vector field

on
 that is never zero, its integral curve
that is never zero, its integral curveIntegral curve
In mathematics, an integral curve is a parametric curve that represents a specific solution to an ordinary differential equation or system of equations...
s will give a 1-dimensional foliation. (i.e. a codimension
 foliation).
foliation).This observation generalises to the Frobenius theorem
Frobenius theorem (differential topology)
In mathematics, Frobenius' theorem gives necessary and sufficient conditions for finding a maximal set of independent solutions of an overdetermined system of first-order homogeneous linear partial differential equations...
, saying that the necessary and sufficient conditions
Necessary and sufficient conditions
In logic, the words necessity and sufficiency refer to the implicational relationships between statements. The assertion that one statement is a necessary and sufficient condition of another means that the former statement is true if and only if the latter is true.-Definitions:A necessary condition...
for a distribution (i.e. an
 dimensional subbundle
dimensional subbundleSubbundle
In mathematics, a subbundle U of a vector bundle V on a topological space X is a collection of linear subspaces Ux of the fibers Vx of V at x in X, that make up a vector bundle in their own right....
of the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
of a manifold) to be tangent to the leaves of a foliation, is that the set of vector fields tangent to the distribution are closed under Lie bracket
Lie bracket
Lie bracket can refer to:*A bilinear binary operation defined on elements of a Lie algebra*Lie bracket of vector fields...
. One can also phrase this differently, as a question of reduction of the structure group
Reduction of the structure group
In mathematics, in particular the theory of principal bundles, one can ask if a G-bundle "comes from" a subgroup H In mathematics, in particular the theory of principal bundles, one can ask if a...
of the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
from
 to a reducible subgroup.
to a reducible subgroup.The conditions in the Frobenius theorem appear as integrability conditions; and the assertion is that if those are fulfilled the reduction can take place because local transition functions with the required block structure
Block structure
* In mathematics, block structure is a possible property of matrices - see block matrix.* In computer science, a programming language has block structure if it features blocks which can be nested to any depth....
exist. For example, in the codimension 1 case, we can define the tangent bundle of the foliation as
 , for some (non-canonical)
, for some (non-canonical)  (ie a non-zero co-vector field). A given
(ie a non-zero co-vector field). A given  is integrable iff
is integrable iff  everywhere.
everywhere.There is a global foliation theory, because topological constraints exist. For example in the surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
case, an everywhere non-zero vector field can exist on an orientable compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
surface only for the torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
. This is a consequence of the Poincaré–Hopf index theorem, which shows the Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
will have to be 0. There are many deep connections with contact topology, which is the "opposite" concept.
Existence of foliations
gave a necessary and sufficient condition for a distribution on a connected non-compact manifold to be homotopic to an integrable distribution. showed that any compact manifold with a distribution has a foliation of the same dimension.See also
- G-structureG-structureIn differential geometry, a G-structure on an n-manifold M, for a given structure group G, is a G-subbundle of the tangent frame bundle FM of M....
- Classifying space for foliations
- Haefliger structureHaefliger structureIn mathematics, a Haefliger structure on a topological space is a generalization of a foliation of a manifold, introduced by . Any foliation on a manifold induces a Haefliger structure, which uniquely determines the foliation.-Definition:...
, a generalization of foliations closed under taking pullbacks. - LaminationLamination (topology)In topology, a branch of mathematics, a lamination is a :* "A topological space partitioned into subsets"* decoration of a manifold in which some subset of the manifold is partitioned into sheets of some lower dimension, and the sheets are locally parallel.Lamination of surface is a partition of...
- Reeb foliationReeb foliationIn mathematics, the Reeb foliation is a particular foliation of the 3-sphere, introduced by the French mathematician Georges Reeb .It is based on dividing the sphere into two solid tori, along a 2-torus: see Clifford torus. Each of the solid tori is then foliated internally, in codimension 1, and...
of the 3-sphere. - Taut foliationTaut foliationIn mathematics, a taut foliation is a codimension 1 foliation of a 3-manifold with the property that there is a single transverse circle intersecting every leaf. By transverse circle, is meant a closed loop that is always transverse to the tangent field of the foliation...

