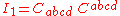Curvature invariant (general relativity)
Encyclopedia
Curvature invariants in general relativity are a set of scalar
s called curvature invariant
s that arise in general relativity
. They are formed from the Riemann, Weyl
and Ricci tensors - which represent curvature
- and possibly operations on them such as contraction, covariant differentiation and dualisation.
Certain invariants formed from these curvature tensors play an important role in classifying spacetime
s. Invariants are actually less powerful for distinguishing locally non-isometric
Lorentzian manifolds than they are for distinguishing Riemannian manifold
s. This means that they are more limited in their applications than for manifolds endowed with a positive definite metric tensor
.
The principal invariants of the Riemann tensor of a four-dimensional Lorentzian manifold are
These are quadratic polynomial invariants (sums of squares of components). (Some authors define the Chern-Pontryagin scalar using the right dual instead of the left dual.)
The first of these was introduced by Erich Kretschmann
. The second two names are somewhat anachronistic, but since the integrals of the last two are related to the instanton number and Euler characteristic
respectively, they have some justification.
The principal invariants of the Weyl tensor
are
(Because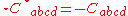 , there is no need to define a third principal invariant for the Weyl tensor.)
, there is no need to define a third principal invariant for the Weyl tensor.)
of the Riemann tensor into the Weyl tensor plus a sum of fourth-rank tensors constructed from the second rank Ricci tensor and from the Ricci scalar, these two sets of invariants are related: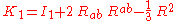

of the Riemann tensor, with respect to a timelike unit vector field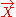 , not necessarily geodesic or hypersurface orthogonal, consists of three pieces
, not necessarily geodesic or hypersurface orthogonal, consists of three pieces
Because these are all transverse (i.e. projected to the spatial hyperplane elements orthogonal to our timelike unit vector field), they can be represented as linear operators on three dimensional vectors, or as three by three real matrices. They are respectively symmetric, traceless, and symmetric (6,8,6 linearly independent components, for a total of 20). If we write these operators as E, B, L respectively, the principal invariants of the Riemann tensor are obtained as follows:
, the principal invariants of the Weyl tensor may be obtained by taking the real and imaginary parts of the expression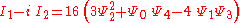
(But note the minus sign!)
The principal quadratic invariant of the Ricci tensor,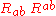 , may be obtained as a more complicated expression involving the Ricci scalars (see the paper by Cherubini et al. cited below).
, may be obtained as a more complicated expression involving the Ricci scalars (see the paper by Cherubini et al. cited below).
is non-compact.
There are still examples of cases when we can distinguish Lorentzian manifolds using their invariants. Examples of such are fully general Petrov type I spacetimes with no Killing vectors, see Coley et al below. Indeed, it was here found that the spacetimes failing to be distinguished by their set of curvature invariants are all Kundt spacetime
s.
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
s called curvature invariant
Curvature invariant
In Riemannian geometry and pseudo-Riemannian geometry, curvature invariants are scalar quantities constructed from tensors that represent curvature...
s that arise in general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
. They are formed from the Riemann, Weyl
Weyl tensor
In differential geometry, the Weyl curvature tensor, named after Hermann Weyl, is a measure of the curvature of spacetime or, more generally, a pseudo-Riemannian manifold. Like the Riemann curvature tensor, the Weyl tensor expresses the tidal force that a body feels when moving along a geodesic...
and Ricci tensors - which represent curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
- and possibly operations on them such as contraction, covariant differentiation and dualisation.
Certain invariants formed from these curvature tensors play an important role in classifying spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
s. Invariants are actually less powerful for distinguishing locally non-isometric
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
Lorentzian manifolds than they are for distinguishing Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
s. This means that they are more limited in their applications than for manifolds endowed with a positive definite metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
.
Principal invariants
The principal invariants of the Riemann and Weyl tensors are certain quadratic polynomial invariants (i.e., sums of squares of components).The principal invariants of the Riemann tensor of a four-dimensional Lorentzian manifold are
- the Kretschmann scalarKretschmann scalarIn the theory of Lorentzian manifolds, particularly in the context of applications to general relativity, the Kretschmann scalar is a quadratic scalar invariant. It was introduced by Erich Kretschmann.-Definition:...

- the Chern-Pontryagin scalar

- the Euler scalar
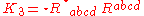
These are quadratic polynomial invariants (sums of squares of components). (Some authors define the Chern-Pontryagin scalar using the right dual instead of the left dual.)
The first of these was introduced by Erich Kretschmann
Erich Kretschmann
Erich Justus Kretschmann was a German physicist.He obtained his D.Phil. at Berlin University in 1914 with his dissertation entitled "Eine Theorie der Schwerkraft im Rahmen der ursprünglichen Einsteinschen Relativitätstheorie "...
. The second two names are somewhat anachronistic, but since the integrals of the last two are related to the instanton number and Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
respectively, they have some justification.
The principal invariants of the Weyl tensor
Weyl tensor
In differential geometry, the Weyl curvature tensor, named after Hermann Weyl, is a measure of the curvature of spacetime or, more generally, a pseudo-Riemannian manifold. Like the Riemann curvature tensor, the Weyl tensor expresses the tidal force that a body feels when moving along a geodesic...
are
(Because
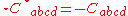 , there is no need to define a third principal invariant for the Weyl tensor.)
, there is no need to define a third principal invariant for the Weyl tensor.)Relation with Ricci decomposition
As one might expect from the Ricci decompositionRicci decomposition
In semi-Riemannian geometry, the Ricci decomposition is a way of breaking up the Riemann curvature tensor of a pseudo-Riemannian manifold into pieces with useful individual algebraic properties...
of the Riemann tensor into the Weyl tensor plus a sum of fourth-rank tensors constructed from the second rank Ricci tensor and from the Ricci scalar, these two sets of invariants are related:
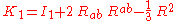

Relation with Bel decomposition
Recall that (in four dimensions), the Bel decompositionBel decomposition
In semi-Riemannian geometry, the Bel decomposition, taken with respect to a specific timelike congruence, is a way of breaking up the Riemann tensor of a pseudo-Riemannian manifold into four pieces. It was introduced in 1959 by the physicist Lluis Bel....
of the Riemann tensor, with respect to a timelike unit vector field
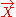 , not necessarily geodesic or hypersurface orthogonal, consists of three pieces
, not necessarily geodesic or hypersurface orthogonal, consists of three pieces
- the electrogravitic tensor

- the magnetogravitic tensor
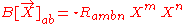
- the topogravitic tensor
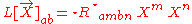
Because these are all transverse (i.e. projected to the spatial hyperplane elements orthogonal to our timelike unit vector field), they can be represented as linear operators on three dimensional vectors, or as three by three real matrices. They are respectively symmetric, traceless, and symmetric (6,8,6 linearly independent components, for a total of 20). If we write these operators as E, B, L respectively, the principal invariants of the Riemann tensor are obtained as follows:
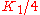 is the trace of E2 + L2 - 2 B BT,
is the trace of E2 + L2 - 2 B BT, is the trace of B ( E - L ),
is the trace of B ( E - L ),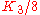 is the trace of E L - B2.
is the trace of E L - B2.
Expression in Newman-Penrose formalism
In terms of the Weyl scalars in the Newman-Penrose formalismNewman-Penrose Formalism
The Newman-Penrose Formalism is a set of notation developed by Ezra T. Newman and Roger Penrose for General Relativity. Their notation is an effort to treat General Relativity in terms of spinor notation, which introduces complex forms of the usual variables used in GR.The NP formalism is itself a...
, the principal invariants of the Weyl tensor may be obtained by taking the real and imaginary parts of the expression
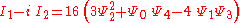
(But note the minus sign!)
The principal quadratic invariant of the Ricci tensor,
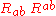 , may be obtained as a more complicated expression involving the Ricci scalars (see the paper by Cherubini et al. cited below).
, may be obtained as a more complicated expression involving the Ricci scalars (see the paper by Cherubini et al. cited below).Distinguishing Lorentzian manifolds
An important question related to Curvature invariants is when the set of polynomial curvature invariants can be used to (locally) distinguish manifolds. To be able to do this is necessary to include higher-order invariants including derivatives of the Riemann tensor but in the Lorentzian case, it is known that there are spacetimes which cannot be distinguished; e.g., the VSI spacetimes for which all such curvature invariants vanish and thus cannot be distinguished from flat space. This failure of being able to distinguishing Lorentzian manifolds is related to the fact that the Lorentz groupLorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
is non-compact.
There are still examples of cases when we can distinguish Lorentzian manifolds using their invariants. Examples of such are fully general Petrov type I spacetimes with no Killing vectors, see Coley et al below. Indeed, it was here found that the spacetimes failing to be distinguished by their set of curvature invariants are all Kundt spacetime
Kundt spacetime
In mathematical physics, Kundt spacetimes are Lorentzian manifolds admitting a geodesic null congruence with vanishing optical scalars . A well known member of Kundt class is pp-wave. Ricci-flat Kundt spacetimes in arbitrary dimension are algebraically special. In four dimensions Ricci-flat ...
s.
See also
- Bach tensorBach tensorIn differential geometry and general relativity, the Bach tensor is a tensor of rank 2 which is conformally invariant in dimension n=4. It is the only known conformally invariant tensor that is algebraically independent of the Weyl tensor...
, for a sometimes useful tensor generated by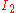 via a variational principle.
via a variational principle. - Carminati-McLenaghan invariantsCarminati-McLenaghan invariantsIn general relativity, the Carminati–McLenaghan invariants or CM scalars are a set of 16 scalar curvature invariants for the Riemann tensor. This set is usually supplemented with at least two additional invariants.-Mathematical definition:...
, for a set of polynomial invariants of the Riemann tensor of a four-dimensional Lorentzian manifold which is known to be complete under some circumstances. - Curvature invariantCurvature invariantIn Riemannian geometry and pseudo-Riemannian geometry, curvature invariants are scalar quantities constructed from tensors that represent curvature...
, for curvature invariants in a more general context.