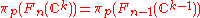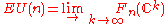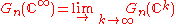Classifying space for U(n)
Encyclopedia
In mathematics
, the classifying space
for the unitary group
U(n) is a space B(U(n)) together with a universal bundle E(U(n)) such that any hermitian bundle on a paracompact space
X is the pull-back of E by a map X → B unique up to homotopy.
This space with its universal fibration may be constructed as either
Both constructions are detailed here.
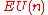 of the universal bundle
of the universal bundle
is given by
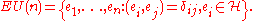
Here, H is an infinite-dimensional complex Hilbert space, the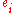 are vectors in H, and
are vectors in H, and 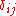 is the Kronecker delta. The symbol
is the Kronecker delta. The symbol  is the inner product on H. Thus, we have that EU(n) is the space of orthonormal n-frames in H.
is the inner product on H. Thus, we have that EU(n) is the space of orthonormal n-frames in H.
The group action
of U(n) on this space is the natural one. The base space is then
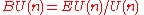
and is the set of Grassmannian
n-dimensional subspaces (or n-planes) in H. That is,
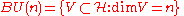
so that V is an n-dimensional vector space.
 , one has
, one has
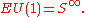
known to be a contractible space.
The base space is then
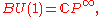
the infinite-dimensional complex projective space
. Thus, the set of isomorphism class
es of circle bundles over a manifold
 are in one-to-one correspondence with the homotopy classes of maps from
are in one-to-one correspondence with the homotopy classes of maps from  to
to 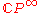 .
.
One also has the relation that
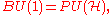
that is, is the infinite-dimensional projective unitary group
is the infinite-dimensional projective unitary group
. See that article for additional discussion and properties.
For a torus
T, which is abstractly isomorphic to , but need not have a chosen identification, one writes
, but need not have a chosen identification, one writes  .
.
The topological K-theory
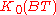 is given by numerical polynomial
is given by numerical polynomial
s; more details below.
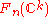 be the space of orthonormal families of
be the space of orthonormal families of  vectors in
vectors in 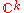 and let
and let 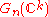 be the Grassmannian of
be the Grassmannian of  -dimensional subvector spaces of
-dimensional subvector spaces of 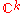 . The total space of the universal bundle can be taken to be the direct limit of the
. The total space of the universal bundle can be taken to be the direct limit of the 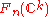 as
as 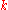 goes to infinity, while the base space is the direct limit of the
goes to infinity, while the base space is the direct limit of the  as
as 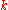 goes to infinity.
goes to infinity.
Let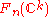 be the space of orthonormal families of
be the space of orthonormal families of  vectors in
vectors in 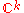 . The group
. The group 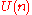 acts
acts
freely on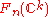 and the quotient is the Grassmannian
and the quotient is the Grassmannian 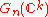 of
of  -dimensional subvector spaces of
-dimensional subvector spaces of 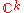 . The map
. The map
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the classifying space
Classifying space
In mathematics, specifically in homotopy theory, a classifying space BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G...
for the unitary group
Unitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
U(n) is a space B(U(n)) together with a universal bundle E(U(n)) such that any hermitian bundle on a paracompact space
Paracompact space
In mathematics, a paracompact space is a topological space in which every open cover admits a locally finite open refinement. Paracompact spaces are sometimes also required to be Hausdorff. Paracompact spaces were introduced by ....
X is the pull-back of E by a map X → B unique up to homotopy.
This space with its universal fibration may be constructed as either
- the GrassmannianGrassmannianIn mathematics, a Grassmannian is a space which parameterizes all linear subspaces of a vector space V of a given dimension. For example, the Grassmannian Gr is the space of lines through the origin in V, so it is the same as the projective space P. The Grassmanians are compact, topological...
of n-planes in an infinite-dimensional complex Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
; or, - the direct limit, with the induced topology, of GrassmannianGrassmannianIn mathematics, a Grassmannian is a space which parameterizes all linear subspaces of a vector space V of a given dimension. For example, the Grassmannian Gr is the space of lines through the origin in V, so it is the same as the projective space P. The Grassmanians are compact, topological...
s of n planes.
Both constructions are detailed here.
Construction as an infinite Grassmannian
The total space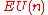 of the universal bundle
of the universal bundleUniversal bundle
In mathematics, the universal bundle in the theory of fiber bundles with structure group a given topological group G, is a specific bundle over a classifying space BG, such that every bundle with the given structure group G over M is a pullback by means of a continuous map-In the CW complex...
is given by
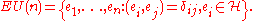
Here, H is an infinite-dimensional complex Hilbert space, the
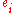 are vectors in H, and
are vectors in H, and 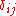 is the Kronecker delta. The symbol
is the Kronecker delta. The symbol  is the inner product on H. Thus, we have that EU(n) is the space of orthonormal n-frames in H.
is the inner product on H. Thus, we have that EU(n) is the space of orthonormal n-frames in H.The group action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of U(n) on this space is the natural one. The base space is then
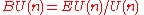
and is the set of Grassmannian
Grassmannian
In mathematics, a Grassmannian is a space which parameterizes all linear subspaces of a vector space V of a given dimension. For example, the Grassmannian Gr is the space of lines through the origin in V, so it is the same as the projective space P. The Grassmanians are compact, topological...
n-dimensional subspaces (or n-planes) in H. That is,
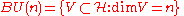
so that V is an n-dimensional vector space.
Case of line bundles
In the case of , one has
, one has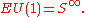
known to be a contractible space.
The base space is then
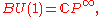
the infinite-dimensional complex projective space
Complex projective space
In mathematics, complex projective space is the projective space with respect to the field of complex numbers. By analogy, whereas the points of a real projective space label the lines through the origin of a real Euclidean space, the points of a complex projective space label the complex lines...
. Thus, the set of isomorphism class
Isomorphism class
An isomorphism class is a collection of mathematical objects isomorphic to each other.Isomorphism classes are often defined if the exact identity of the elements of the set is considered irrelevant, and the properties of the structure of the mathematical object are studied. Examples of this are...
es of circle bundles over a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
 are in one-to-one correspondence with the homotopy classes of maps from
are in one-to-one correspondence with the homotopy classes of maps from  to
to 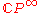 .
.One also has the relation that
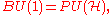
that is,
 is the infinite-dimensional projective unitary group
is the infinite-dimensional projective unitary groupProjective unitary group
In mathematics, the projective unitary group PU is the quotient of the unitary group U by the right multiplication of its center, U, embedded as scalars....
. See that article for additional discussion and properties.
For a torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
T, which is abstractly isomorphic to
 , but need not have a chosen identification, one writes
, but need not have a chosen identification, one writes  .
.The topological K-theory
Topological K-theory
In mathematics, topological K-theory is a branch of algebraic topology. It was founded to study vector bundles on general topological spaces, by means of ideas now recognised as K-theory that were introduced by Alexander Grothendieck...
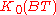 is given by numerical polynomial
is given by numerical polynomialNumerical polynomial
In mathematics, a numerical polynomial is a polynomial with rational coefficients that takes integer values on integers. They are also called integer-valued polynomials....
s; more details below.
Construction as an inductive limit
Let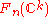 be the space of orthonormal families of
be the space of orthonormal families of  vectors in
vectors in 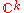 and let
and let 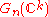 be the Grassmannian of
be the Grassmannian of  -dimensional subvector spaces of
-dimensional subvector spaces of 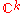 . The total space of the universal bundle can be taken to be the direct limit of the
. The total space of the universal bundle can be taken to be the direct limit of the 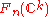 as
as 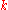 goes to infinity, while the base space is the direct limit of the
goes to infinity, while the base space is the direct limit of the  as
as 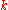 goes to infinity.
goes to infinity.Validity of the construction
In this section, we will define the topology on EU(n) and prove that EU(n) is indeed contractible.Let
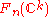 be the space of orthonormal families of
be the space of orthonormal families of  vectors in
vectors in 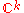 . The group
. The group 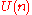 acts
actsfreely on
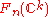 and the quotient is the Grassmannian
and the quotient is the Grassmannian 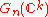 of
of  -dimensional subvector spaces of
-dimensional subvector spaces of 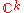 . The map
. The map-
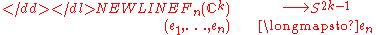
is a fibre bundle of fibre . Thus because
. Thus because  is trivial and because of the long exact sequence of the fibrationHomotopy groupIn mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
is trivial and because of the long exact sequence of the fibrationHomotopy groupIn mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
, we have
whenever . By taking
. By taking 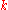 big enough, precisely for
big enough, precisely for  , we can repeat the process and get
, we can repeat the process and get
This last group is trivial for k > n + p. Let
be the direct limitDirect limitIn mathematics, a direct limit is a colimit of a "directed family of objects". We will first give the definition for algebraic structures like groups and modules, and then the general definition which can be used in any category.- Algebraic objects :In this section objects are understood to be...
of all the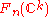 (with the induced topology). Let
(with the induced topology). Let
be the direct limitDirect limitIn mathematics, a direct limit is a colimit of a "directed family of objects". We will first give the definition for algebraic structures like groups and modules, and then the general definition which can be used in any category.- Algebraic objects :In this section objects are understood to be...
of all the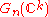 (with the induced topology).
(with the induced topology).
Lemma
The group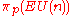 is trivial for all
is trivial for all  .
.
Proof
Let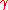 be a map from the sphere
be a map from the sphere 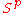 to EU(n). As
to EU(n). As 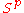 is compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
is compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
,
there exists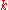 such that
such that 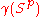 is included in
is included in 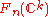 . By taking
. By taking 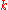 big enough,
big enough,
we see that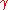 is homotopic, with respect to the base point, to the constant map.
is homotopic, with respect to the base point, to the constant map.

In addition,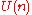 acts freely on
acts freely on 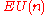 . The spaces
. The spaces 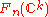 and
and 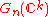 are CW-complexesCW complexIn topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
are CW-complexesCW complexIn topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
. One can
find a decomposition of these spaces into CW-complexes such that the decomposition of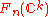 , resp.
, resp.
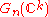 , is induced by restriction of the one for
, is induced by restriction of the one for 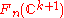 , resp.
, resp. 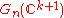 . Thus
. Thus 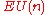 (and also
(and also 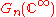 ) is a CW-complex. By
) is a CW-complex. By
Whitehead TheoremWhitehead theoremIn homotopy theory , the Whitehead theorem states that if a continuous mapping f between topological spaces X and Y induces isomorphisms on all homotopy groups, then f is a homotopy equivalence provided X and Y are connected and have the homotopy-type of CW complexes. This result was proved by J....
and the above Lemma,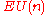 is contractible.
is contractible.
Cohomology of
Proposition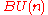
The cohomologyCohomologyIn mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
of the classifying space is a ringRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
is a ringRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
of polynomials in variables
variables
 where
where  is of degree
is of degree 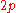 .
.
Proof
Let us first consider the case . In this case,
. In this case, 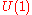 is the circle
is the circle 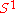 and the universal bundle
and the universal bundle
is . It is well known that the cohomology of
. It is well known that the cohomology of
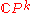 is isomorphic to
is isomorphic to 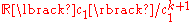 , where
, where 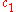 is the Euler classEuler classIn mathematics, specifically in algebraic topology, the Euler class, named after Leonhard Euler, is a characteristic class of oriented, real vector bundles. Like other characteristic classes, it measures how "twisted" the vector bundle is...
is the Euler classEuler classIn mathematics, specifically in algebraic topology, the Euler class, named after Leonhard Euler, is a characteristic class of oriented, real vector bundles. Like other characteristic classes, it measures how "twisted" the vector bundle is...
of
the -bundle
-bundle  , and that the injections
, and that the injections  ,
,
for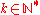 , are compatible with these presentations of the cohomology of the projective spaces.
, are compatible with these presentations of the cohomology of the projective spaces.
This proves the Proposition for .
.
In the general case, let be the subgroup of diagonal matrices. It is a maximal torusMaximal torusIn the mathematical theory of compact Lie groups a special role is played by torus subgroups, in particular by the maximal torus subgroups.A torus in a Lie group G is a compact, connected, abelian Lie subgroup of G . A maximal torus is one which is maximal among such subgroups...
be the subgroup of diagonal matrices. It is a maximal torusMaximal torusIn the mathematical theory of compact Lie groups a special role is played by torus subgroups, in particular by the maximal torus subgroups.A torus in a Lie group G is a compact, connected, abelian Lie subgroup of G . A maximal torus is one which is maximal among such subgroups...
in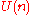 . Its
. Its
classifying space is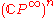 and its cohomology is
and its cohomology is  , where
, where
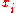 is the Euler classEuler classIn mathematics, specifically in algebraic topology, the Euler class, named after Leonhard Euler, is a characteristic class of oriented, real vector bundles. Like other characteristic classes, it measures how "twisted" the vector bundle is...
is the Euler classEuler classIn mathematics, specifically in algebraic topology, the Euler class, named after Leonhard Euler, is a characteristic class of oriented, real vector bundles. Like other characteristic classes, it measures how "twisted" the vector bundle is...
of the tautological bundle over the i-th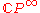 . The
. The
Weyl groupWeyl groupIn mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
acts on by permuting the diagonal entries, hence it acts on
by permuting the diagonal entries, hence it acts on 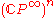 by
by
permutation of the factors. The induced action on its cohomology is the permutation of the
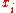 's. We deduce
's. We deduce
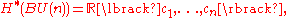
where the 's are the symmetric polynomials in the
's are the symmetric polynomials in the 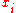 's.
's.

K-theory of
The topological K-theory Topological K-theoryIn mathematics, topological K-theory is a branch of algebraic topology. It was founded to study vector bundles on general topological spaces, by means of ideas now recognised as K-theory that were introduced by Alexander Grothendieck...
Topological K-theoryIn mathematics, topological K-theory is a branch of algebraic topology. It was founded to study vector bundles on general topological spaces, by means of ideas now recognised as K-theory that were introduced by Alexander Grothendieck...
is known explicitly in terms of numericalNumerical polynomialIn mathematics, a numerical polynomial is a polynomial with rational coefficients that takes integer values on integers. They are also called integer-valued polynomials....
symmetric polynomialSymmetric polynomialIn mathematics, a symmetric polynomial is a polynomial P in n variables, such that if any of the variables are interchanged, one obtains the same polynomial...
s.
The K-theory reduces to computing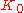 , since K-theory is 2-periodic by the Bott periodicity theoremBott periodicity theoremIn mathematics, the Bott periodicity theorem describes a periodicity in the homotopy groups of classical groups, discovered by , which proved to be of foundational significance for much further research, in particular in K-theory of stable complex vector bundles, as well as the stable homotopy...
, since K-theory is 2-periodic by the Bott periodicity theoremBott periodicity theoremIn mathematics, the Bott periodicity theorem describes a periodicity in the homotopy groups of classical groups, discovered by , which proved to be of foundational significance for much further research, in particular in K-theory of stable complex vector bundles, as well as the stable homotopy...
, and
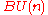 is a limit of complex manifolds, so it has a CW-structure with only cells in even dimensions, so odd K-theory vanishes.
is a limit of complex manifolds, so it has a CW-structure with only cells in even dimensions, so odd K-theory vanishes.
Thus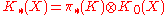 , where
, where 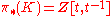 , where t is the Bott generator.
, where t is the Bott generator.
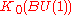 is the ring of numerical polynomialNumerical polynomialIn mathematics, a numerical polynomial is a polynomial with rational coefficients that takes integer values on integers. They are also called integer-valued polynomials....
is the ring of numerical polynomialNumerical polynomialIn mathematics, a numerical polynomial is a polynomial with rational coefficients that takes integer values on integers. They are also called integer-valued polynomials....
s in w, regarded as a subring of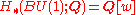 , where w is element dual to tautological bundle.
, where w is element dual to tautological bundle.
For the n-torus, is numerical polynomials in n variables.
is numerical polynomials in n variables.
The map is onto, via a splitting principleSplitting principleIn mathematics, the splitting principle is a technique used to reduce questions about vector bundles to the case of line bundles.In the theory of vector bundles, one often wishes to simplify computations, say of Chern classes. Often computations are well understood for line bundles and for direct...
is onto, via a splitting principleSplitting principleIn mathematics, the splitting principle is a technique used to reduce questions about vector bundles to the case of line bundles.In the theory of vector bundles, one often wishes to simplify computations, say of Chern classes. Often computations are well understood for line bundles and for direct...
, as is the maximal torusMaximal torusIn the mathematical theory of compact Lie groups a special role is played by torus subgroups, in particular by the maximal torus subgroups.A torus in a Lie group G is a compact, connected, abelian Lie subgroup of G . A maximal torus is one which is maximal among such subgroups...
is the maximal torusMaximal torusIn the mathematical theory of compact Lie groups a special role is played by torus subgroups, in particular by the maximal torus subgroups.A torus in a Lie group G is a compact, connected, abelian Lie subgroup of G . A maximal torus is one which is maximal among such subgroups...
of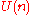 . The map is the symmetrization map
. The map is the symmetrization map
and the image can be identified as the symmetric polynomials satisfying the integrality condition that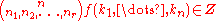
where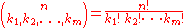
is the multinomial coefficient and contains r distinct integers, repeated
contains r distinct integers, repeated  times, respectively.
times, respectively.
-