Direct limit
Encyclopedia
In mathematics
, a direct limit (also called inductive limit) is a colimit
of a "directed family of objects". We will first give the definition for algebraic structure
s like groups
and modules
, and then the general definition which can be used in any category
.
such as groups
, rings
, modules
(over a fixed ring), algebras
(over a fixed field), etc. With this in mind, homomorphism
s are understood in the corresponding setting (group homomorphism
s, etc.).
Start with the definition of a direct system of objects and homomorphisms. Let be a directed set
be a directed set
. Let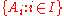 be a family of objects indexed
be a family of objects indexed
by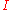 and
and 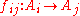 be a homomorphism for all
be a homomorphism for all  with the following properties:
with the following properties:
Then the pair is called a direct system over
is called a direct system over  .
.
The underlying set of the direct limit, , of the direct system
, of the direct system 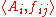 is defined as the disjoint union
is defined as the disjoint union
of the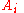 's modulo
's modulo
a certain equivalence relation
 :
: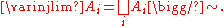
Here, if and
and  ,
,  if there is some
if there is some  such that
such that 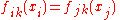 .
.
Heuristically, two elements in the disjoint union are equivalent if and only if
they "eventually become equal" in the direct system. An equivalent formulation that highlights the duality to the inverse limit
is that an element is equivalent to all its images under the maps of the directed system, i.e. .
.
One naturally obtains from this definition canonical morphisms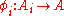 sending each element to its equivalence class. The algebraic operations on
sending each element to its equivalence class. The algebraic operations on  are defined via these maps in the obvious manner.
are defined via these maps in the obvious manner.
An important property is that taking direct limits in the category of modules
is an exact functor
.
 by means of a universal property
by means of a universal property
. Let be a direct system of objects and morphisms in
be a direct system of objects and morphisms in  (same definition as above). The direct limit of this system is an object
(same definition as above). The direct limit of this system is an object 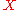 in
in  together with morphisms
together with morphisms 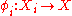 satisfying
satisfying  . The pair
. The pair 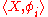 must be universal in the sense that for any other such pair
must be universal in the sense that for any other such pair  there exists a unique morphism
there exists a unique morphism  making the diagram
making the diagram
commute
for all i, j. The direct limit is often denoted
with the direct system being understood.
being understood.
Unlike for algebraic objects, the direct limit may not exist in an arbitrary category. If it does, however, it is unique in a strong sense: given another direct limit X′ there exists a unique isomorphism
X′ → X commuting with the canonical morphisms.
We note that a direct system in a category admits an alternative description in terms of functor
admits an alternative description in terms of functor
s. Any directed poset can be considered as a small category
can be considered as a small category  where the morphisms consist of arrows
where the morphisms consist of arrows  if and only if
if and only if
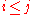 . A direct system is then just a covariant functor
. A direct system is then just a covariant functor  .
.
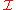 and
and  categories. Let
categories. Let 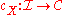 be a constant functor with fixed object
be a constant functor with fixed object  . Define for every functor
. Define for every functor  the functor
the functor
which assigns to each the set
the set 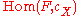 of natural transformations from F to
of natural transformations from F to  . If
. If 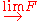 is representable
is representable
, the representing object in is called the direct limit of F and is also denoted by
is called the direct limit of F and is also denoted by  .
.
If is an abelian category
is an abelian category
where arbitrary (also infinite) direct sums of objects exists (this is Grothedieck's Axiom AB3). Then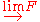 is representable for every functor
is representable for every functor  and
and
is a right-exact
additive functor of abelian categories.
of the direct limit is called the inverse limit
(or projective limit). More general concepts are the limits and colimits
of category theory. The terminology is somewhat confusing: direct limits are colimits while inverse limits are limits.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a direct limit (also called inductive limit) is a colimit
Limit (category theory)
In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products and inverse limits....
of a "directed family of objects". We will first give the definition for algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
s like groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
and modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
, and then the general definition which can be used in any category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
.
Algebraic objects
In this section objects are understood to be sets with a given algebraic structureAlgebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
such as groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, rings
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
(over a fixed ring), algebras
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
(over a fixed field), etc. With this in mind, homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
s are understood in the corresponding setting (group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
s, etc.).
Start with the definition of a direct system of objects and homomorphisms. Let
 be a directed set
be a directed setDirected set
In mathematics, a directed set is a nonempty set A together with a reflexive and transitive binary relation ≤ , with the additional property that every pair of elements has an upper bound: In other words, for any a and b in A there must exist a c in A with a ≤ c and b ≤...
. Let
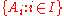 be a family of objects indexed
be a family of objects indexedIndex set
In mathematics, the elements of a set A may be indexed or labeled by means of a set J that is on that account called an index set...
by
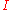 and
and 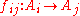 be a homomorphism for all
be a homomorphism for all  with the following properties:
with the following properties:
-
 is the identity of
is the identity of 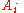 , and
, and -
 for all
for all  .
.
Then the pair
 is called a direct system over
is called a direct system over  .
.The underlying set of the direct limit,
 , of the direct system
, of the direct system 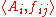 is defined as the disjoint union
is defined as the disjoint unionDisjoint union
In mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
of the
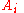 's modulo
's moduloModulo (jargon)
The word modulo is the Latin ablative of modulus which itself means "a small measure."It was introduced into mathematics in the book Disquisitiones Arithmeticae by Carl Friedrich Gauss in 1801...
a certain equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
 :
: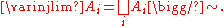
Here, if
 and
and  ,
,  if there is some
if there is some  such that
such that 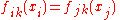 .
.Heuristically, two elements in the disjoint union are equivalent if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
they "eventually become equal" in the direct system. An equivalent formulation that highlights the duality to the inverse limit
Inverse limit
In mathematics, the inverse limit is a construction which allows one to "glue together" several related objects, the precise manner of the gluing process being specified by morphisms between the objects...
is that an element is equivalent to all its images under the maps of the directed system, i.e.
 .
.One naturally obtains from this definition canonical morphisms
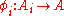 sending each element to its equivalence class. The algebraic operations on
sending each element to its equivalence class. The algebraic operations on  are defined via these maps in the obvious manner.
are defined via these maps in the obvious manner.An important property is that taking direct limits in the category of modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
is an exact functor
Exact functor
In homological algebra, an exact functor is a functor, from some category to another, which preserves exact sequences. Exact functors are very convenient in algebraic calculations, roughly speaking because they can be applied to presentations of objects easily...
.
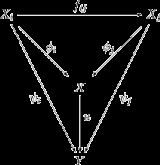
Direct limit over a direct system in a category
The direct limit can be defined in an arbitrary categoryCategory (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
 by means of a universal property
by means of a universal propertyUniversal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
. Let
 be a direct system of objects and morphisms in
be a direct system of objects and morphisms in  (same definition as above). The direct limit of this system is an object
(same definition as above). The direct limit of this system is an object 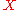 in
in  together with morphisms
together with morphisms 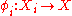 satisfying
satisfying  . The pair
. The pair 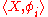 must be universal in the sense that for any other such pair
must be universal in the sense that for any other such pair  there exists a unique morphism
there exists a unique morphism  making the diagram
making the diagramcommute
Commutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
for all i, j. The direct limit is often denoted

with the direct system
 being understood.
being understood.Unlike for algebraic objects, the direct limit may not exist in an arbitrary category. If it does, however, it is unique in a strong sense: given another direct limit X′ there exists a unique isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
X′ → X commuting with the canonical morphisms.
We note that a direct system in a category
 admits an alternative description in terms of functor
admits an alternative description in terms of functorFunctor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
s. Any directed poset
 can be considered as a small category
can be considered as a small category  where the morphisms consist of arrows
where the morphisms consist of arrows  if and only if
if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
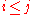 . A direct system is then just a covariant functor
. A direct system is then just a covariant functor  .
.General Definition
Let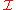 and
and  categories. Let
categories. Let 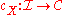 be a constant functor with fixed object
be a constant functor with fixed object  . Define for every functor
. Define for every functor  the functor
the functor
which assigns to each
 the set
the set 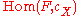 of natural transformations from F to
of natural transformations from F to  . If
. If 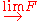 is representable
is representableRepresentable functor
In mathematics, particularly category theory, a representable functor is a functor of a special form from an arbitrary category into the category of sets. Such functors give representations of an abstract category in terms of known structures In mathematics, particularly category theory, a...
, the representing object in
 is called the direct limit of F and is also denoted by
is called the direct limit of F and is also denoted by  .
.If
 is an abelian category
is an abelian categoryAbelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
where arbitrary (also infinite) direct sums of objects exists (this is Grothedieck's Axiom AB3). Then
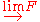 is representable for every functor
is representable for every functor  and
and
is a right-exact
Exact functor
In homological algebra, an exact functor is a functor, from some category to another, which preserves exact sequences. Exact functors are very convenient in algebraic calculations, roughly speaking because they can be applied to presentations of objects easily...
additive functor of abelian categories.
Examples
- A collection of subsets
 of a set M can be partially ordered by inclusion. If the collection is directed, its direct limit is the union
of a set M can be partially ordered by inclusion. If the collection is directed, its direct limit is the union 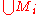 .
. - Let I be any directed set with a greatest elementGreatest elementIn mathematics, especially in order theory, the greatest element of a subset S of a partially ordered set is an element of S which is greater than or equal to any other element of S. The term least element is defined dually...
m. The direct limit of any corresponding direct system is isomorphic to Xm and the canonical morphism φm: Xm → X is an isomorphism. - Let p be a prime numberPrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
. Consider the direct system composed of the groups Z/pnZ and the homomorphisms Z/pnZ → Z/pn+1Z which are induced by multiplication by p. The direct limit of this system consists of all the roots of unity of order some power of p, and is called the Prüfer groupPrüfer groupIn mathematics, specifically in group theory, the Prüfer p-group or the p-quasicyclic group or p∞-group, Z, for a prime number p is the unique p-group in which every element has p pth roots. The group is named after Heinz Prüfer...
Z(p∞). - Let F be a C-valued sheafSheaf (mathematics)In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
on a topological spaceTopological spaceTopological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X. Fix a point x in X. The open neighborhoods of x form a directed poset ordered by inclusion (U ≤ V if and only if U contains V). The corresponding direct system is (F(U), rU,V) where r is the restriction map. The direct limit of this system is called the stalk of F at x, denoted Fx. For each neighborhood U of x, the canonical morphism F(U) → Fx associates to a section s of F over U an element sx of the stalk Fx called the germGerm (mathematics)In mathematics, the notion of a germ of an object in/on a topological space captures the local properties of the object. In particular, the objects in question are mostly functions and subsets...
of s at x. - Direct limits in the category of topological spacesCategory of topological spacesIn mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous...
are given by placing the final topologyFinal topologyIn general topology and related areas of mathematics, the final topology on a set X, with respect to a family of functions into X, is the finest topology on X which makes those functions continuous.- Definition :Given a set X and a family of topological spaces Y_i with functionsf_i: Y_i \to Xthe...
on the underlying set-theoretic direct limit. - Inductive limits are linked to projective ones via

- Consider a sequence {An, φn} where An is a C*-algebra and φn : An → An + 1 is a *-homomorphism. The C*-analog of the direct limit construction gives a C*-algebra satisfying the universal property above.
Related constructions and generalizations
The categorical dualDual (category theory)
In category theory, a branch of mathematics, duality is a correspondence between properties of a category C and so-called dual properties of the opposite category Cop...
of the direct limit is called the inverse limit
Inverse limit
In mathematics, the inverse limit is a construction which allows one to "glue together" several related objects, the precise manner of the gluing process being specified by morphisms between the objects...
(or projective limit). More general concepts are the limits and colimits
Limit (category theory)
In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products and inverse limits....
of category theory. The terminology is somewhat confusing: direct limits are colimits while inverse limits are limits.

