
Paracompact space
Encyclopedia
In mathematics
, a paracompact space is a topological space
in which every open cover admits a locally finite
open refinement. Paracompact spaces are sometimes also required to be Hausdorff
. Paracompact spaces were introduced by .
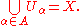

Note the similarity between the definitions of compact
and paracompact: for paracompact, we replace "subcover" by "open refinement" and "finite" by "locally finite". Both of these changes are significant: if we take the above definition of paracompact and change "open refinement" back to "subcover", or "locally finite" back to "finite", we end up with the compact spaces in both cases.
A hereditarily paracompact space is a space such that every subspace of it is paracompact. This is equivalent to requiring that every open subspace be paracompact.
Some examples of spaces that are not paracompact include:
s is that they are normal
and admit partitions of unity subordinate to any open cover. This means the following: if X is a paracompact Hausdorff space with a given open cover, then there exists a collection of continuous functions on X with values in the unit interval
[0, 1] such that:
In fact, a Hausdorff space is paracompact if and only if it admits partitions of unity subordinate to any open cover (see below). This property is sometimes used to define paracompact spaces (at least in the Hausdorff case).
Partitions of unity are useful because they often allow one to extend local constructions to the whole space. For instance, the integral of differential form
s on paracompact manifold
s is first defined locally (where the manifold looks like Euclidean space
and the integral is well known), and this definition is then extended to the whole space via a partition of unity.
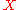 is paracompact if and only if it every open cover admits a subordinate partition of unity. The if direction is straightforward. Now for the only if direction, we do this in a few stages.
is paracompact if and only if it every open cover admits a subordinate partition of unity. The if direction is straightforward. Now for the only if direction, we do this in a few stages.
It is different in these respects:
Both these results can be proved by the tube lemma
which is used in the proof that a product of finitely many compact spaces is compact.

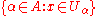
A topological space is:
The adverb "countably" can be added to any of the adjectives "paracompact", "metacompact", and "fully normal" to make the requirement apply only to countable open covers.
Every paracompact space is metacompact, and every metacompact space is orthocompact.
As the name implies, a fully normal space is normal
. Every fully T4 space is paracompact. In fact, for Hausdorff spaces, paracompactness and full normality are equivalent. Thus, a fully T4 space is the same thing as a paracompact Hausdorff space.
As an historical note: fully normal spaces were defined before paracompact spaces.
The proof that all metrizable spaces are fully normal is easy. When it was proved by A.H. Stone that for Hausdorff spaces fully normal and paracompact are equivalent, he implicitly proved that all metrizable spaces are paracompact. Later M.E. Rudin
gave a direct proof of the latter fact.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a paracompact space is a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
in which every open cover admits a locally finite
Locally finite collection
In the mathematical field of topology, local finiteness is a property of collections of subsets of a topological space. It is fundamental in the study of paracompactness and topological dimension....
open refinement. Paracompact spaces are sometimes also required to be Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
. Paracompact spaces were introduced by .
Definitions of relevant terms
- A cover of a set X is a collection of subsetSubsetIn mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of X whose unionUnion (set theory)In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
is X. In symbols, if U = {Uα : α in A} is an indexed family of subsets of X, then U is a cover if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
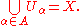
- A cover of a topological space X is open if all its members are open setOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s. In symbols, a cover U is an open cover if U is a subset of T, where T is the topology on X. - A refinement of a cover of a space X is a new cover of the same space such that every set in the new cover is a subsetSubsetIn mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of some set in the old cover. In symbols, the cover V = {Vβ : β in B} is a refinement of the cover U = {Uα : α in A} if and only if, for anyUniversal quantificationIn predicate logic, universal quantification formalizes the notion that something is true for everything, or every relevant thing....
Vβ in V, there exists someExistential quantificationIn predicate logic, an existential quantification is the predication of a property or relation to at least one member of the domain. It is denoted by the logical operator symbol ∃ , which is called the existential quantifier...
Uα in U such that Vβ is contained in Uα. - An open cover of a space X is locally finite if every point of the space has a neighborhood which intersects only finitely many sets in the cover. In symbols, U = {Uα : α in A} is locally finite if and only if, for any x in X, there exists some neighbourhood V(x) of x such that the set

- is finite.
- A topological space X is called paracompact if any open cover of X admits an open refinement that is locally finite.
Note the similarity between the definitions of compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
and paracompact: for paracompact, we replace "subcover" by "open refinement" and "finite" by "locally finite". Both of these changes are significant: if we take the above definition of paracompact and change "open refinement" back to "subcover", or "locally finite" back to "finite", we end up with the compact spaces in both cases.
A hereditarily paracompact space is a space such that every subspace of it is paracompact. This is equivalent to requiring that every open subspace be paracompact.
Examples and counterexamples
- Every compact spaceCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
is paracompact. - (Theorem of A. H. Stone) Every metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
is paracompact. Early proofs were somewhat involved, but an elementary one was found by M. E. RudinMary Ellen RudinMary Ellen Rudin is an American mathematician.Born Mary Ellen Estill, she attended the University of Texas, completing her B.A. in 1944 and her Ph.D. in 1949, under Robert Lee Moore. In 1953, she married the mathematician Walter Rudin. Following her mentor Moore, her research centers on point-set...
. Existing proofs of this require the axiom of choice for the non-separable case. It has been shown that neither ZF theoryZermelo–Fraenkel set theoryIn mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
nor ZF theory with the axiom of dependent choiceAxiom of dependent choiceIn mathematics, the axiom of dependent choices, denoted DC, is a weak form of the axiom of choice which is still sufficient to develop most of real analysis...
is sufficient. - Every regularRegular spaceIn topology and related fields of mathematics, a topological space X is called a regular space if every non-empty closed subset C of X and a point p not contained in C admit non-overlapping open neighborhoods. Thus p and C...
Lindelöf spaceLindelöf spaceIn mathematics, a Lindelöf space is a topological space in which every open cover has a countable subcover. The Lindelöf property is a weakening of the more commonly used notion of compactness, which requires the existence of a finite subcover....
is paracompact. In particular, every locally compact HausdorffHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
second-countable spaceSecond-countable spaceIn topology, a second-countable space, also called a completely separable space, is a topological space satisfying the second axiom of countability. A space is said to be second-countable if its topology has a countable base...
is paracompact. - The Sorgenfrey line is paracompact, even though it is neither compact, locally compact, second countable, nor metrizable.
- Every CW complexCW complexIn topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
is paracompact
Some examples of spaces that are not paracompact include:
- The most famous counterexample is the long lineLong line (topology)In topology, the long line is a topological space somewhat similar to the real line, but in a certain way "longer". It behaves locally just like the real line, but has different large-scale properties. Therefore it serves as one of the basic counterexamples of topology...
, which is a nonparacompact topological manifoldTopological manifoldIn mathematics, a topological manifold is a topological space which looks locally like Euclidean space in a sense defined below...
. (The long line is locally compact, but not second countable.) - Another counterexample is a productProduct topologyIn topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
of uncountablyUncountable setIn mathematics, an uncountable set is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related to its cardinal number: a set is uncountable if its cardinal number is larger than that of the set of all natural numbers.-Characterizations:There...
many copies of an infinite discrete spaceDiscrete spaceIn topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
. Any infinite set carrying the particular point topologyParticular point topologyIn mathematics, the particular point topology is a topology where sets are considered open if they are empty or contain a particular, arbitrarily chosen, point of the topological space. Formally, let X be any set and p ∈ X. The collectionof subsets of X is then the particular point topology...
is not paracompact; in fact it is not even metacompact. - The Prüfer manifoldPrüfer manifoldIn mathematics, the Prüfer manifold or Prüfer surface is a 2-dimensional Hausdorff real analytic manifold that is not paracompact. It was introduced by and named after Heinz Prüfer.-Construction:The Prüfer manifold can be constructed as follows...
is a non-paracompact surface.
Properties
- (Theorem of Jean DieudonnéJean DieudonnéJean Alexandre Eugène Dieudonné was a French mathematician, notable for research in abstract algebra and functional analysis, for close involvement with the Nicolas Bourbaki pseudonymous group and the Éléments de géométrie algébrique project of Alexander Grothendieck, and as a historian of...
) Every paracompact Hausdorff space is normalNormal spaceIn topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
. - Paracompactness is weakly hereditary, i.e. every closed subspace of a paracompact space is paracompact. This can be extended to F-sigmaF-sigma setIn mathematics, an Fσ set is a countable union of closed sets. The notation originated in France with F for fermé and σ for somme ....
subspaces as well. - If every open subset of a space is paracompact, then it is hereditarily paracompact.
- A regular spaceRegular spaceIn topology and related fields of mathematics, a topological space X is called a regular space if every non-empty closed subset C of X and a point p not contained in C admit non-overlapping open neighborhoods. Thus p and C...
is paracompact if every open cover admits a locally finite refinement. (Here, the refinement is not required to be open.) In particular, every regular Lindelof spaceLindelöf spaceIn mathematics, a Lindelöf space is a topological space in which every open cover has a countable subcover. The Lindelöf property is a weakening of the more commonly used notion of compactness, which requires the existence of a finite subcover....
is paracompact. - (Smirnov metrization theorem) A topological space is metrizable if and only if it is paracompact, Hausdorff, and locally metrizable.
- Every paracompact Hausdorff space is a shrinking spaceShrinking spaceIn mathematics, in the field of topology, a topological space is said to be a shrinking space if every open cover admits a shrinking. A shrinking of an open cover is another open cover indexed by the same indexing set, with the property that the closure of each open set in the shrinking lies inside...
, that is, every open cover of a paracompact Hausdorff space has a shrinking: another open cover indexed by the same set such that the closure of every set in the new cover lies inside the corresponding set in the old cover. - On paracompact Hausdorff spaces, the cohomology of a sheaf is equal to its Čech cohomologyCech cohomologyIn mathematics, specifically algebraic topology, Čech cohomology is a cohomology theory based on the intersection properties of open covers of a topological space. It is named for the mathematician Eduard Čech.-Motivation:...
. - Michael selection theoremMichael selection theoremIn functional analysis, a branch of mathematics, the most popular version of the Michael selection theorem, named after Ernest Michael, states the following:- Other selection theorems :* Zero-dimensional Michael selection theorem...
states that lower semicontinuous multifunctions from X into nonempty closed convex subsets of Banach spaces admit continuous selection iff X is paracompact.
Partitions of unity
Paracompactness has little to do with the notion of compactness, but rather more to do with breaking up topological space entities into manageable pieces. The most important feature of paracompact Hausdorff spaceHausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
s is that they are normal
Normal space
In topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
and admit partitions of unity subordinate to any open cover. This means the following: if X is a paracompact Hausdorff space with a given open cover, then there exists a collection of continuous functions on X with values in the unit interval
Unit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
[0, 1] such that:
- for every function f: X → R from the collection, there is an open set U from the cover such that the supportSupport (mathematics)In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
of f is contained in U; - for every point x in X, there is a neighborhood V of x such that all but finitely many of the functions in the collection are identically 0 in V and the sum of the nonzero functions is identically 1 in V.
In fact, a Hausdorff space is paracompact if and only if it admits partitions of unity subordinate to any open cover (see below). This property is sometimes used to define paracompact spaces (at least in the Hausdorff case).
Partitions of unity are useful because they often allow one to extend local constructions to the whole space. For instance, the integral of differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s on paracompact manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s is first defined locally (where the manifold looks like Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
and the integral is well known), and this definition is then extended to the whole space via a partition of unity.
Proof that paracompact hausdorff spaces admit partitions of unity
An hausdorff space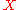 is paracompact if and only if it every open cover admits a subordinate partition of unity. The if direction is straightforward. Now for the only if direction, we do this in a few stages.
is paracompact if and only if it every open cover admits a subordinate partition of unity. The if direction is straightforward. Now for the only if direction, we do this in a few stages.- Lemma 1: If
 is a locally finite open cover, then there exists open sets
is a locally finite open cover, then there exists open sets  for each
for each  , such that each
, such that each 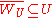 and
and  is a locally finite refinement.
is a locally finite refinement.
- Lemma 2: If
 is a locally finite open cover, then there are continuous functions
is a locally finite open cover, then there are continuous functions 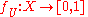 such that
such that  and such that
and such that  is a continuous function which is always non-zero and finite.
is a continuous function which is always non-zero and finite.
- Theorem: In a paracompact hausdorff space
 , if
, if  is an open cover, then there exists a partition of unity subordinate to it.
is an open cover, then there exists a partition of unity subordinate to it.
- Proof (Lemma 1): Let
 be the collection of open sets meeting only finitely many sets in
be the collection of open sets meeting only finitely many sets in  , and whose closure is contained in a set in
, and whose closure is contained in a set in  . One can check as an exercise that this provides an open refinement, since paracompact hausdorff spaces are regular, and since
. One can check as an exercise that this provides an open refinement, since paracompact hausdorff spaces are regular, and since  is locally finite. Now replace
is locally finite. Now replace 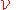 by a locally finite open refinitement. One can easily check that each set in this refinement has the same property as that which characterised the original cover.
by a locally finite open refinitement. One can easily check that each set in this refinement has the same property as that which characterised the original cover.
- Now we define
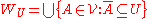 . We have that each
. We have that each 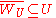 ; for otherwise letting
; for otherwise letting  , we take
, we take 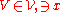 with closure contained in
with closure contained in  ; but then
; but then  a contradiction. And it easy to see that
a contradiction. And it easy to see that  is an open refinement of
is an open refinement of  .
.
- Finally, to verify that this cover is locally finite, fix
 ; let
; let  a neighbourhood of
a neighbourhood of  meeting only finitely many sets in
meeting only finitely many sets in  . We will show that
. We will show that  meets only finitely many of the
meets only finitely many of the 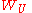 . If
. If  meets
meets  , then some
, then some  with
with  meets
meets  . Thus
. Thus  is the same as
is the same as  which is contained in
which is contained in  . By the setup of
. By the setup of  , each
, each  meets only finitely many sets in
meets only finitely many sets in  . Hence the right-hand collection is a finite union of finite sets. Thus
. Hence the right-hand collection is a finite union of finite sets. Thus 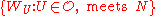 is finite. Hence the cover is locally finite.
is finite. Hence the cover is locally finite.
- Proof (Lemma 2): Applying Lemma 1, let
 be coninuous maps with
be coninuous maps with  and
and  (by Urysohn's lemma for disjoint closed sets in normal spaces, which a paracompact hausdorff space is). Note by the support of a function, we here mean the points not mapping to zero (and not the closure of this set). To show that
(by Urysohn's lemma for disjoint closed sets in normal spaces, which a paracompact hausdorff space is). Note by the support of a function, we here mean the points not mapping to zero (and not the closure of this set). To show that  is always finite and non-zero, take
is always finite and non-zero, take  , and let
, and let  a neighbourhood of
a neighbourhood of  meeting only finitely many sets in
meeting only finitely many sets in  ; thus
; thus  belongs to only finitely many sets in
belongs to only finitely many sets in  ; thus
; thus  for all but finitely many
for all but finitely many 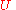 ; moreover
; moreover  for some
for some  , thus
, thus 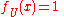 ; so
; so  is finite and
is finite and  . To establish continuity, take
. To establish continuity, take  as before, and let
as before, and let 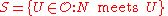 , which is finite; then
, which is finite; then 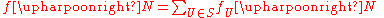 , which is a continuous function; hence the preimage under
, which is a continuous function; hence the preimage under  of a neighbourhood of
of a neighbourhood of  will be a neighbourhood of
will be a neighbourhood of  .
.
- Proof (Theorem): Take
 a locally finite subcover of the refinement cover:
a locally finite subcover of the refinement cover:  . Applying Lemma 2, we obtain continuous functions
. Applying Lemma 2, we obtain continuous functions 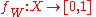 with
with  (thus the usual closed version of the support is contained in some
(thus the usual closed version of the support is contained in some  , for each
, for each 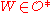 ; for which their sum constitutes a continuous function which is always finite non-zero (hence
; for which their sum constitutes a continuous function which is always finite non-zero (hence  is continuous positive, finite-valued). So replacing each
is continuous positive, finite-valued). So replacing each  by
by  , we have now — all things remaining the same — that their sum is everywhere
, we have now — all things remaining the same — that their sum is everywhere  . Finally for
. Finally for  , letting
, letting  be a neighbourhood of
be a neighbourhood of  meeting only finitely many sets in
meeting only finitely many sets in  , we have
, we have  for all but finitely many
for all but finitely many  since each
since each  . Thus we have a partition of unity subordinate to the original open cover.
. Thus we have a partition of unity subordinate to the original open cover.
Comparison with compactness
Paracompactness is similar to compactness in the following respects:- Every closed subset of a paracompact space is paracompact.
- Every paracompact Hausdorff space is normal.
It is different in these respects:
- A paracompact subset of a Hausdorff space need not be closed. In fact, for metric spaces, all subsets are paracompact.
- A product of paracompact spaces need not be paracompact. The square of the real line R in the lower limit topology is a classical example for this.
Product related properties
Although a product of paracompact spaces need not be paracompact, the following are true:- The product of a paracompact space and a compact spaceCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
is paracompact. - The product of a metacompact spaceMetacompact spaceIn mathematics, in the field of general topology, a topological space is said to be metacompact if every open cover has a point finite open refinement...
and a compact space is metacompact.
Both these results can be proved by the tube lemma
Tube lemma
In mathematics, particularly topology, the tube lemma is a useful tool in order to prove that the finite product of compact spaces is compact. It is in general, a concept of point-set topology.-Tube lemma:...
which is used in the proof that a product of finitely many compact spaces is compact.
Variations
There are several variations of the notion of paracompactness. To define them, we first need to extend the list of terms above:- Given a cover and a point, the star of the point in the cover is the union of all the sets in the cover that contain the point. In symbols, the star of x in U = {Uα : α in A} is

- The notation for the star is not standardised in the literature, and this is just one possibility.
- A star refinementStar refinementIn mathematics, specifically in the study of topology and open covers of a topological space X, a star refinement is a particular kind of refinement of an open cover of X....
of a cover of a space X is a new cover of the same space such that, given any point in the space, the star of the point in the new cover is a subset of some set in the old cover. In symbols, V is a star refinement of U = {Uα : α in A} if and only if, for any x in X, there exists a Uα in U, such that V*(x) is contained in Uα. - A cover of a space X is pointwise finite if every point of the space belongs to only finitely many sets in the cover. In symbols, U is pointwise finite if and only if, for any x in X, the set
- A star refinement
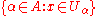
- is finite.
A topological space is:
- metacompactMetacompact spaceIn mathematics, in the field of general topology, a topological space is said to be metacompact if every open cover has a point finite open refinement...
if every open cover has an open pointwise finite refinement. - orthocompactOrthocompact spaceIn mathematics, in the field of general topology, a topological space is said to be orthocompact if every open cover has an interior preserving open refinement...
if every open cover has an open refinement such that the intersection of all the open sets about any point in this refinement is open. - fully normal if every open cover has an open star refinement, and fully T4 if it is fully normal and T1T1 spaceIn topology and related branches of mathematics, a T1 space is a topological space in which, for every pair of distinct points, each has an open neighborhood not containing the other. An R0 space is one in which this holds for every pair of topologically distinguishable points...
(see separation axioms).
The adverb "countably" can be added to any of the adjectives "paracompact", "metacompact", and "fully normal" to make the requirement apply only to countable open covers.
Every paracompact space is metacompact, and every metacompact space is orthocompact.
As the name implies, a fully normal space is normal
Normal space
In topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
. Every fully T4 space is paracompact. In fact, for Hausdorff spaces, paracompactness and full normality are equivalent. Thus, a fully T4 space is the same thing as a paracompact Hausdorff space.
As an historical note: fully normal spaces were defined before paracompact spaces.
The proof that all metrizable spaces are fully normal is easy. When it was proved by A.H. Stone that for Hausdorff spaces fully normal and paracompact are equivalent, he implicitly proved that all metrizable spaces are paracompact. Later M.E. Rudin
Mary Ellen Rudin
Mary Ellen Rudin is an American mathematician.Born Mary Ellen Estill, she attended the University of Texas, completing her B.A. in 1944 and her Ph.D. in 1949, under Robert Lee Moore. In 1953, she married the mathematician Walter Rudin. Following her mentor Moore, her research centers on point-set...
gave a direct proof of the latter fact.

