
Whitehead theorem
Encyclopedia
In homotopy theory the Whitehead theorem states that if a continuous mapping f between topological space
s X and Y induces isomorphisms on all homotopy group
s, then f is a homotopy equivalence provided X and Y are connected
and have the homotopy-type of CW complex
es. This result was proved by J. H. C. Whitehead
in two landmark papers from 1949, and provides a justification for working with the CW complex
concept that he introduced there.
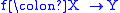
such that f(x) = y, we consider for n ≥ 0 the induced homomorphisms
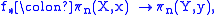
where πn denotes for n ≥ 1 the n-th homotopy group. For n = 0 this means the mapping of the path-connected components; if we assume both X and Y are connected we can ignore this as containing no information. We say that f is a weak homotopy equivalence if the homomorphisms f* are all isomorphisms. The Whitehead theorem then states that a weak homotopy equivalence, for connected CW complexes, is a homotopy equivalence
.
× RP3
and Y= RP² × S³. Then X and Y have the same fundamental group, namely Z2, and the same universal cover, namely S² × S³; thus, they have isomorphic homotopy groups. On the other hand their homology groups are different (as can be seen from the Künneth formula
); thus, X and Y are not homotopy equivalent.
The Whitehead theorem does not hold for general topological spaces or even for all subspaces of Rn. For example, the Warsaw circle, a subset of the plane, has all homotopy groups zero, but the map from the Warsaw circle to a single point is not a homotopy equivalence. The study of possible generalizations of Whitehead's theorem to more general spaces is part of the subject of shape theory
.
, a weak equivalence between cofibrant-fibrant objects is a homotopy equivalence.
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s X and Y induces isomorphisms on all homotopy group
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
s, then f is a homotopy equivalence provided X and Y are connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
and have the homotopy-type of CW complex
CW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
es. This result was proved by J. H. C. Whitehead
J. H. C. Whitehead
John Henry Constantine Whitehead FRS , known as Henry, was a British mathematician and was one of the founders of homotopy theory. He was born in Chennai , in India, and died in Princeton, New Jersey, in 1960....
in two landmark papers from 1949, and provides a justification for working with the CW complex
CW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
concept that he introduced there.
Statement
More accurately, we suppose given CW complexes X and Y, with respective base points x and y. Given a continuous mapping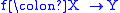
such that f(x) = y, we consider for n ≥ 0 the induced homomorphisms
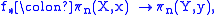
where πn denotes for n ≥ 1 the n-th homotopy group. For n = 0 this means the mapping of the path-connected components; if we assume both X and Y are connected we can ignore this as containing no information. We say that f is a weak homotopy equivalence if the homomorphisms f* are all isomorphisms. The Whitehead theorem then states that a weak homotopy equivalence, for connected CW complexes, is a homotopy equivalence
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
.
Spaces with isomorphic homotopy groups may not be homotopy equivalent
A word of caution: it is not enough to assume πn(X) is isomorphic to πn(Y) for each n ≥ 1 in order to conclude that X and Y are homotopy equivalent. One really needs a map f : X → Y inducing such isomorphisms in homotopy. For instance, take X= S2Hypersphere
In mathematics, an n-sphere is a generalization of the surface of an ordinary sphere to arbitrary dimension. For any natural number n, an n-sphere of radius r is defined as the set of points in -dimensional Euclidean space which are at distance r from a central point, where the radius r may be any...
× RP3
Real projective space
In mathematics, real projective space, or RPn, is the topological space of lines through 0 in Rn+1. It is a compact, smooth manifold of dimension n, and a special case of a Grassmannian.-Construction:...
and Y= RP² × S³. Then X and Y have the same fundamental group, namely Z2, and the same universal cover, namely S² × S³; thus, they have isomorphic homotopy groups. On the other hand their homology groups are different (as can be seen from the Künneth formula
Künneth theorem
In mathematics, especially in homological algebra and algebraic topology, a Künneth theorem is a statement relating the homology of two objects to the homology of their product. The classical statement of the Künneth theorem relates the singular homology of two topological spaces X and Y and their...
); thus, X and Y are not homotopy equivalent.
The Whitehead theorem does not hold for general topological spaces or even for all subspaces of Rn. For example, the Warsaw circle, a subset of the plane, has all homotopy groups zero, but the map from the Warsaw circle to a single point is not a homotopy equivalence. The study of possible generalizations of Whitehead's theorem to more general spaces is part of the subject of shape theory
Shape theory (mathematics)
Shape theory is a branch of the mathematical field of topology. Homotopy theory is not appropriate for spaces with bad local properties, hence the need for replacement of homotopy theory by a more sophisticated approach...
.
Generalization to model categories
In any model categoryModel category
In mathematics, particularly in homotopy theory, a model category is a category with distinguished classes of morphisms called 'weak equivalences', 'fibrations' and 'cofibrations'. These abstract from a conventional homotopy category, of topological spaces or of chain complexes...
, a weak equivalence between cofibrant-fibrant objects is a homotopy equivalence.

