Bump function
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a bump function is a function
on a Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
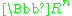which is both smoothSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
(in the sense of having continuous derivatives of all orders) and compactly supported. The space of all bump functions on
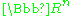is denoted 
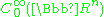or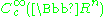 
. The dual spaceDual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
of this space endowed with a suitable topology is the space of distributions
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
.
Examples
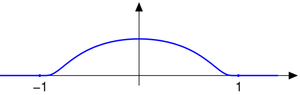
given by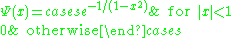
is an example of a bump function in one dimension. It is clear from the construction that this function has compact support. The proof of smoothness follows along the same lines as for the related function discussed in the Non-analytic smooth function
Non-analytic smooth function
In mathematics, smooth functions and analytic functions are two very important types of functions. One can easily prove that any analytic function of a real argument is smooth...
article. This function can be interpreted as the Gaussian function
scaled to fit into the unit disc: the substitution 
corresponds to sending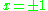 
to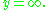 
A simple example of a bump function in
variables is obtained by taking the product of 
copies of the above bump function in one variable, so
Existence of bump functions
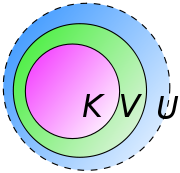
is an arbitrary compact set in n dimensions and 
is an open setOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
containing
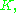there exists a bump function 
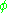which is 1 on 
and 0 outside of 
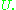Since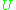 
can be taken to be a very small neighborhood of 
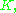this amounts to being able to construct a function that is 1 on 
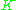and falls off rapidly to 0 outside of 
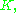while still being smooth.The construction proceeds as follows. One considers a compact neighborhood
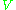of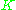 
contained in 
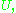so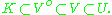 
The characteristic function 
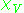of 
will be equal to 1 on 
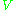and 
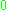outside of 
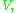so in particular, it will be 1 on 
and 
outside of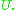 
This function is not smooth however. The key idea is to smooth 
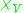a bit, by taking the convolutionConvolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
of
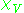with a mollifierMollifier
In mathematics, mollifiers are smooth functions with special properties, used in distribution theory to create sequences of smooth functions approximating nonsmooth functions, via convolution...
. The latter is just a bump function with a very small support and whose integral is 1. Such a mollifier can be obtained, for example, by taking the bump function
from the previous section and performing appropriate scalings.Properties and uses
While bump functions are smooth, they cannot be analyticAnalytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
unless they vanish identically. This is a simple consequence of the identity theorem
Identity theorem
In complex analysis, a branch of mathematics, the identity theorem for holomorphic functions states: given functions f and g holomorphic on a connected open set D, if f = g on some neighborhood of z that is in D, then f = g on D. Thus a holomorphic function is completely determined by its values on...
.
Bump functions are often used as mollifier
Mollifier
In mathematics, mollifiers are smooth functions with special properties, used in distribution theory to create sequences of smooth functions approximating nonsmooth functions, via convolution...
s, as smooth cutoff functions, and to form smooth partitions of unity. They are the most common class of test functions used in analysis.
The space of bump functions is closed under many operations. For instance, the sum, product, or convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
of two bump functions is again a bump function, and any differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
with smooth coefficients, when applied to a bump function, will produce another bump function.
The Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of a bump function is a Schwartz function, but cannot be compactly supported unless it is zero, since it is an entire analytic function (see Paley–Wiener theorem
Paley–Wiener theorem
In mathematics, a Paley–Wiener theorem is any theorem that relates decay properties of a function or distribution at infinity with analyticity of its Fourier transform. The theorem is named for Raymond Paley and Norbert Wiener . The original theorems did not use the language of distributions,...
). Because the bump function is infinitely differentiable, its Fourier transform F(k) must decay faster than any finite power of 1/k for a large angular frequency |k|. The Fourier transform of the particular bump function
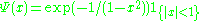from above can be analyzed by a saddle-point method, and decays asymptotically as 
for large |k|.