Equality (mathematics) - AbsoluteAstronomy.com

Loosely, equality is the state of being quantitatively the same. More formally, equality (or the identity relation) is the binary relation

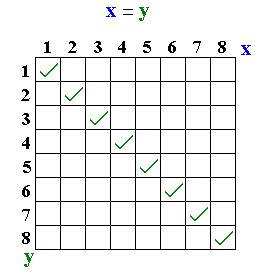
Binary relation

In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...

on a set X defined by

.

The identity relation is the archetype of the more general concept of an equivalence relation

Equivalence relation

In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...

on a set: those binary relations which are reflexive

Reflexive relation

In mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...

, symmetric

Symmetric relation

In mathematics, a binary relation R over a set X is symmetric if it holds for all a and b in X that if a is related to b then b is related to a.In mathematical notation, this is:...

, and transitive

Transitive relation

In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....

. The relation of equality is also antisymmetric

Antisymmetric relation

In mathematics, a binary relation R on a set X is antisymmetric if, for all a and b in Xor, equivalently,In mathematical notation, this is:\forall a, b \in X,\ R \and R \; \Rightarrow \; a = bor, equivalently,...

. These four properties uniquely determine the equality relation on any set S and render equality the only relation on S that is both an equivalence relation and a partial order. It follows from this that equality is the smallest equivalence relation on any set S, in the sense that it is a subset

Subset

In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...

of any other equivalence relation on S. An equation

Equation

An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...

is simply an assertion

Logical assertion

A logical assertion is a statement that asserts that a certain premise is true, and is useful for statements in proof. It is equivalent to a sequent with an empty antecedent....

that two expression

Expression (mathematics)

In mathematics, an expression is a finite combination of symbols that is well-formed according to rules that depend on the context. Symbols can designate numbers , variables, operations, functions, and other mathematical symbols, as well as punctuation, symbols of grouping, and other syntactic...

s are related by equality (are equal).

In weakly typed programming languages like C

C (programming language)

C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....

, a logical operation of equality test often yields a value value of 1 or 0 or is automatically converted in such a value if the environment requires this. The mathematical equivalent of such operation is Kronecker delta. Languages with stronger type systems (like Java

Java (programming language)

Java is a programming language originally developed by James Gosling at Sun Microsystems and released in 1995 as a core component of Sun Microsystems' Java platform. The language derives much of its syntax from C and C++ but has a simpler object model and fewer low-level facilities...

) often have a dedicated Boolean data type.

The etymology of the word is from the Latin aequalis, meaning uniform or identical, from aequus, meaning "level, even, or just."

Logical formulations

The equality relation is always defined such that things that are equal have all and only the same properties. Some people define equality as congruence. Often equality is just defined as identity

Identity (philosophy)

In philosophy, identity, from , is the relation each thing bears just to itself. According to Leibniz's law two things sharing every attribute are not only similar, but are the same thing. The concept of sameness has given rise to the general concept of identity, as in personal identity and...

.

A stronger sense of equality is obtained if some form of Leibniz's law is added as an axiom

Axiom

In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...

; the assertion of this axiom rules out "bare particulars"—things that have all and only the same properties but are not equal to each other—which are possible in some logical formalisms. The axiom states that two things are equal if they have all and only the same properties

Property (philosophy)

In modern philosophy, logic, and mathematics a property is an attribute of an object; a red object is said to have the property of redness. The property may be considered a form of object in its own right, able to possess other properties. A property however differs from individual objects in that...

. Formally:

Given any x and y, x = y if, given any predicate P, P(x) if and only if

If and only if

In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....

P(y).

In this law, the connective "if and only if" can be weakened to "if"; the modified law is equivalent to the original.

Instead of considering Leibniz's law as an axiom, it can also be taken as the definition of equality. The property of being an equivalence relation, as well as the properties given below, can then be proved: they become theorem

Theorem

In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...

s.
If a=b, then a can replace b and b can replace a.

Some basic logical properties of equality

The substitution property states:

For any quantities a and b and any expression F(x), if a = b, then F(a) = F(b) (if either side makes sense, i.e. is well-formed
Well-formed formula
In mathematical logic, a well-formed formula, shortly wff, often simply formula, is a word which is part of a formal language...

).

In first-order logic

First-order logic

First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...

, this is a schema, since we can't quantify over expressions like F (which would be a functional predicate

Functional predicate

In formal logic and related branches of mathematics, a functional predicate, or function symbol, is a logical symbol that may be applied to an object term to produce another object term....

).

Some specific examples of this are:

For any real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s a, b, and c, if a = b, then a + c = b + c (here F(x) is x + c);
For any real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s a, b, and c, if a = b, then a − c = b − c (here F(x) is x − c);
For any real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s a, b, and c, if a = b, then ac = bc (here F(x) is xc);
For any real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s a, b, and c, if a = b and c is not
Division by zero
In mathematics, division by zero is division where the divisor is zero. Such a division can be formally expressed as a / 0 where a is the dividend . Whether this expression can be assigned a well-defined value depends upon the mathematical setting...

zero
0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...

, then a/c = b/c (here F(x) is x/c).

The reflexive property states:

For any quantity a, a = a.

This property is generally used in mathematical proof

Mathematical proof

In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...

s as an intermediate step.

The symmetric property states:

For any quantities a and b, if a = b, then b = a.

The transitive property states:

For any quantities a, b, and c, if a = b and b = c, then a = c.

The binary relation

Binary relation

"is approximately equal

Approximation

An approximation is a representation of something that is not exact, but still close enough to be useful. Although approximation is most often applied to numbers, it is also frequently applied to such things as mathematical functions, shapes, and physical laws.Approximations may be used because...

" between real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s or other things, even if more precisely defined, is not transitive (it may seem so at first sight, but many small difference

Difference

Difference may refer to:* Difference , a 2005 power metal album* Difference , a concept in computer science* Difference , any systematic way of distinguishing similar coats of arms belonging to members of the same family* Difference , a statement about the relative size or order of two objects**...

s can add up to something big).
However, equality almost everywhere

Almost everywhere

In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...

is transitive.

Although the symmetric and transitive properties are often seen as fundamental, they can be proved, if the substitution and reflexive properties are assumed instead.

Relation with equivalence and isomorphism

In some contexts, equality is sharply distinguished from equivalence
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...

or isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...

. For example, one may distinguish fractions
Fraction (mathematics)
A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, we specify how many parts of a certain size there are, for example, one-half, five-eighths and three-quarters.A common or "vulgar" fraction, such as 1/2, 5/8, 3/4, etc., consists...

from rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...

s, the latter being equivalence classes of fractions: the fractions

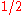and

are distinct as fractions, as different strings of symbols, but they "represent" the same rational number, the same point on a number line. This distinction gives rise to the notion of a quotient set.

Similarly, the sets

and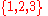

are not equal sets – the first consists of letters, while the second consists of numbers – but they are both sets of three elements, and thus isomorphic, meaning that there is a bijection

Bijection

A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...

between them, for example

However, there are other choices of isomorphism, such as

and these sets cannot be identified without making such a choice – any statement that identifies them "depends on choice of identification". This distinction, between equality and isomorphism, is of fundamental importance in category theory

Category theory

Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...

, and is one motivation for the development of category theory.

Logical formulations

Some basic logical properties of equality

Relation with equivalence and isomorphism

See also