
Annulus (mathematics)
Encyclopedia
In mathematics
, an annulus (the Latin
word for "little ring", with plural annuli) is a ring-shaped geometric figure, or more generally, a term used to name a ring-shaped object. Or, it is the area between two concentric circles. The adjectival form is annular (for example, an annular eclipse).
The open annulus is topologically equivalent to both the open cylinder
and the punctured plane.
The area of an annulus is the difference in the areas of the larger circle
of radius and the smaller one of radius :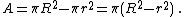
The area of an annulus can be obtained from the length of the longest interval that can lie completely inside the annulus, 2*d in the accompanying diagram. This can be proven by the Pythagorean theorem
; the length of the longest interval that can lie completely inside the annulus will be tangent
to the smaller circle and form a right angle with its radius at that point. Therefore d and r are the sides of a right angled triangle with hypotenuse R and the area is given by: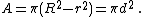
The area can also be obtained via calculus
by dividing the annulus up into an infinite number of annuli of infinitesimal
width and area and then integrating
from ρ = r to ρ = R: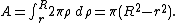
an annulus in the complex plane
is an open region defined by:
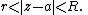
If is , the region is known as the punctured disk of radius around the point .
As a subset of the complex plane
, an annulus can be considered as a Riemann surface
. The complex structure of an annulus depends only on the ratio . Each annulus can be holomorphically
mapped to a standard one centered at the origin and with outer radius by the map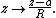
The inner radius is then .
The Hadamard three-circle theorem
is a statement about the maximum value a holomorphic function may take inside an annulus.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an annulus (the Latin
Latin
Latin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...
word for "little ring", with plural annuli) is a ring-shaped geometric figure, or more generally, a term used to name a ring-shaped object. Or, it is the area between two concentric circles. The adjectival form is annular (for example, an annular eclipse).
The open annulus is topologically equivalent to both the open cylinder
Cylinder (geometry)
A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder...
and the punctured plane.
The area of an annulus is the difference in the areas of the larger circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
of radius and the smaller one of radius :
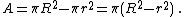
The area of an annulus can be obtained from the length of the longest interval that can lie completely inside the annulus, 2*d in the accompanying diagram. This can be proven by the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
; the length of the longest interval that can lie completely inside the annulus will be tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
to the smaller circle and form a right angle with its radius at that point. Therefore d and r are the sides of a right angled triangle with hypotenuse R and the area is given by:
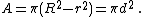
The area can also be obtained via calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
by dividing the annulus up into an infinite number of annuli of infinitesimal
Infinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
width and area and then integrating
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
from ρ = r to ρ = R:
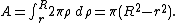
Complex structure
In complex analysisComplex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
an annulus in the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
is an open region defined by:
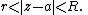
If is , the region is known as the punctured disk of radius around the point .
As a subset of the complex plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
, an annulus can be considered as a Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
. The complex structure of an annulus depends only on the ratio . Each annulus can be holomorphically
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
mapped to a standard one centered at the origin and with outer radius by the map
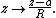
The inner radius is then .
The Hadamard three-circle theorem
Hadamard three-circle theorem
In complex analysis, a branch of mathematics, theHadamard three-circle theorem is a result about the behavior of holomorphic functions.Let f be a holomorphic function on the annulusr_1\leq\left| z\right| \leq r_3....
is a statement about the maximum value a holomorphic function may take inside an annulus.
External links
- Annulus definition and properties With interactive animation
- Area of an annulus, formula With interactive animation

