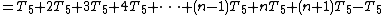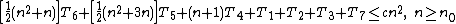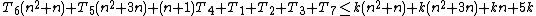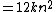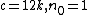Analysis of algorithms
Encyclopedia
To analyze an algorithm is to determine the amount of resources (such as time and storage) necessary to execute it. Most algorithm
s are designed to work with inputs of arbitrary length. Usually the efficiency or running time of an algorithm is stated as a function relating the input length to the number of steps (time complexity
) or storage locations (space complexity).
Algorithm analysis is an important part of a broader computational complexity theory
, which provides theoretical estimates for the resources needed by any algorithm which solves a given computational problem. These estimates provide an insight into reasonable directions of search for efficient algorithms.
In theoretical analysis of algorithms it is common to estimate their complexity in the asymptotic sense, i.e., to estimate the complexity function for arbitrarily large input. Big O notation
, omega notation and theta notation are used to this end. For instance, binary search is said to run in a number of steps proportional to the logarithm of the length of the list being searched, or in O(log(n)), colloquially "in logarithmic time". Usually asymptotic
estimates are used because different implementation
s of the same algorithm may differ in efficiency. However the efficiencies of any two "reasonable" implementations of a given algorithm are related by a constant multiplicative factor called a hidden constant.
Exact (not asymptotic) measures of efficiency can sometimes be computed but they usually require certain assumptions concerning the particular implementation of the algorithm, called model of computation
. A model of computation may be defined in terms of an abstract computer
, e.g., Turing machine
, and/or by postulating that certain operations are executed in unit time.
For example, if the sorted list to which we apply binary search has n elements, and we can guarantee that each lookup of an element in the list can be done in unit time, then at most log2 n + 1 time units are needed to return an answer.
Two cost models are generally used:
The latter is more cumbersome to use, so it's only employed when necessary, for example in the analysis of arbitrary-precision arithmetic
algorithms, like those used in cryptography
.
A key point which is often overlooked is that published lower bounds for problems are often given for a model of computation that is more restricted than the set of operations that you could use in practice and therefore there are algorithms that are faster than what would naively be thought possible.
(or run-time) of an algorithm
as its input size
(usually denoted as n) increases. Run-time efficiency is a topic of great interest in computer science
: A program
can take seconds, hours or even years to finish executing, depending on which algorithm it implements (see also performance analysis
, which is the analysis of an algorithm's run-time in practice).
on an arbitrary computer
running an arbitrary operating system
), there are significant drawbacks to using an empirical
approach to gauge the comparative performance of a given set of algorithms.
Take as an example a program that looks up a specific entry in a sorted
list of size n. Suppose this program were implemented on Computer A, a state-of-the-art machine, using a linear search
algorithm, and on Computer B, a much slower machine, using a binary search algorithm. Benchmark testing
on the two computers running their respective programs might look something like the following:
Based on these metrics, it would be easy to jump to the conclusion that Computer A is running an algorithm that is far superior in efficiency to that of Computer B. However, if the size of the input-list is increased to a sufficient number, that conclusion is dramatically demonstrated to be in error:
Computer A, running the linear search program, exhibits a linear
growth rate. The program's run-time is directly proportional to its input size. Doubling the input size doubles the run time, quadrupling the input size quadruples the run-time, and so forth. On the other hand, Computer B, running the binary search program, exhibits a logarithm
ic growth rate. Doubling the input size only increases the run time by a constant amount (in this example, 25,000 ns). Even though Computer A is ostensibly a faster machine, Computer B will inevitably surpass Computer A in run-time because it's running an algorithm with a much slower growth rate.
if beyond a certain input size n, the function f(n) times a positive constant provides an upper bound or limit
for the run-time of that algorithm. In other words, for a given input size n greater than some n0 and a constant c, the running time of that algorithm will never be larger than c × f(n). This concept is frequently expressed using Big O notation. For example, since the run-time of insertion sort
grows quadratically
as its input size increases, insertion sort can be said to be of order O(n²).
Big O notation is a convenient way to express the worst-case scenario
for a given algorithm, although it can also be used to express the average-case — for example, the worst-case scenario for quicksort is O(n²), but the average-case run-time is O(n log n).
:
1 get a positive integer from input
2 if n > 10
3 print "This might take a while..."
4 for i = 1 to n
5 for j = 1 to i
6 print i * j
7 print "Done!"
A given computer will take a discrete amount of time
to execute each of the instructions involved with carrying out this algorithm. The specific amount of time to carry out a given instruction will vary depending on which instruction is being executed and which computer is executing it, but on a conventional computer, this amount will be deterministic
. Say that the actions carried out in step 1 are considered to consume time T1, step 2 uses time T2, and so forth.
In the algorithm above, steps 1, 2 and 7 will only be run once. For a worst-case evaluation, it should be assumed that step 3 will be run as well. Thus the total amount of time to run steps 1-3 and step 7 is:
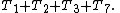
The loops in steps 4, 5 and 6 are trickier to evaluate. The outer loop test in step 4 will execute ( n + 1 )
times (note that an extra step is required to terminate the for loop, hence n + 1 and not n executions), which will consume T4( n + 1 ) time. The inner loop, on the other hand, is governed by the value of i, which iterates
from 1 to n. On the first pass through the outer loop, j iterates from 1 to 1: The inner loop makes one pass, so running the inner loop body (step 6) consumes T6 time, and the inner loop test (step 5) consumes 2T5 time. During the next pass through the outer loop, j iterates from 1 to 2: the inner loop makes two passes, so running the inner loop body (step 6) consumes 2T6 time, and the inner loop test (step 5) consumes 3T5 time.
Altogether, the total time required to run the inner loop body can be expressed as an arithmetic progression
:
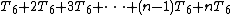
which can be factored
as
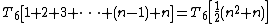
The total time required to run the inner loop test can be evaluated similarly:
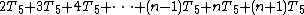
which can be factored as
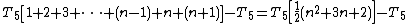
Therefore the total running time for this algorithm is:
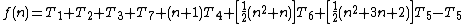
which reduces
to

As a rule-of-thumb, one can assume that the highest-order term in any given function dominates its rate of growth and thus defines its run-time order. In this example, n² is the highest-order term, so one can conclude that f(n) = O(n²). Formally this can be proven as follows:
A more elegant
approach to analyzing this algorithm would be to declare that [T1..T7] are all equal to one unit of time greater than or equal to [T1..T7]. This would mean that the algorithm's running time breaks down as follows:
. As an example, consider the following pseudocode which manages and reallocates memory usage by a program based on the size of a file
which that program manages:
while (file still open)
let n = size of file
for every 100,000 kilobyte
s of increase in file size
double the amount of memory reserved
In this instance, as the file size n increases, memory will be consumed at an exponential growth
rate, which is order O(2n).
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s are designed to work with inputs of arbitrary length. Usually the efficiency or running time of an algorithm is stated as a function relating the input length to the number of steps (time complexity
Time complexity
In computer science, the time complexity of an algorithm quantifies the amount of time taken by an algorithm to run as a function of the size of the input to the problem. The time complexity of an algorithm is commonly expressed using big O notation, which suppresses multiplicative constants and...
) or storage locations (space complexity).
Algorithm analysis is an important part of a broader computational complexity theory
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, which provides theoretical estimates for the resources needed by any algorithm which solves a given computational problem. These estimates provide an insight into reasonable directions of search for efficient algorithms.
In theoretical analysis of algorithms it is common to estimate their complexity in the asymptotic sense, i.e., to estimate the complexity function for arbitrarily large input. Big O notation
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
, omega notation and theta notation are used to this end. For instance, binary search is said to run in a number of steps proportional to the logarithm of the length of the list being searched, or in O(log(n)), colloquially "in logarithmic time". Usually asymptotic
Asymptotic analysis
In mathematical analysis, asymptotic analysis is a method of describing limiting behavior. The methodology has applications across science. Examples are...
estimates are used because different implementation
Implementation
Implementation is the realization of an application, or execution of a plan, idea, model, design, specification, standard, algorithm, or policy.-Computer Science:...
s of the same algorithm may differ in efficiency. However the efficiencies of any two "reasonable" implementations of a given algorithm are related by a constant multiplicative factor called a hidden constant.
Exact (not asymptotic) measures of efficiency can sometimes be computed but they usually require certain assumptions concerning the particular implementation of the algorithm, called model of computation
Model of computation
In computability theory and computational complexity theory, a model of computation is the definition of the set of allowable operations used in computation and their respective costs...
. A model of computation may be defined in terms of an abstract computer
Abstract machine
An abstract machine, also called an abstract computer, is a theoretical model of a computer hardware or software system used in automata theory...
, e.g., Turing machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
, and/or by postulating that certain operations are executed in unit time.
For example, if the sorted list to which we apply binary search has n elements, and we can guarantee that each lookup of an element in the list can be done in unit time, then at most log2 n + 1 time units are needed to return an answer.
Cost models
Time efficiency estimates depend on what we define to be a step. For the analysis to correspond usefully to the actual execution time, the time required to perform a step must be guaranteed to be bounded above by a constant. One must be careful here; for instance, some analyses count an addition of two numbers as one step. This assumption may not be warranted in certain contexts. For example, if the numbers involved in a computation may be arbitrarily large, the time required by a single addition can no longer be assumed to be constant.Two cost models are generally used:
- the uniform cost model, also called uniform-cost measurement (and similar variations), assigns a constant cost to every machine operation, regardless of the size of the numbers involved
- the logarithmic cost model, also called logarithmic-cost measurement (and variations thereof), assigns a cost to every machine operation proportional to the number of bits involved
The latter is more cumbersome to use, so it's only employed when necessary, for example in the analysis of arbitrary-precision arithmetic
Arbitrary-precision arithmetic
In computer science, arbitrary-precision arithmetic indicates that calculations are performed on numbers whose digits of precision are limited only by the available memory of the host system. This contrasts with the faster fixed-precision arithmetic found in most ALU hardware, which typically...
algorithms, like those used in cryptography
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
.
A key point which is often overlooked is that published lower bounds for problems are often given for a model of computation that is more restricted than the set of operations that you could use in practice and therefore there are algorithms that are faster than what would naively be thought possible.
Run-time analysis
Run-time analysis is a theoretical classification that estimates and anticipates the increase in running timeDTIME
In computational complexity theory, DTIME is the computational resource of computation time for a deterministic Turing machine. It represents the amount of time that a "normal" physical computer would take to solve a certain computational problem using a certain algorithm...
(or run-time) of an algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
as its input size
Information
Information in its most restricted technical sense is a message or collection of messages that consists of an ordered sequence of symbols, or it is the meaning that can be interpreted from such a message or collection of messages. Information can be recorded or transmitted. It can be recorded as...
(usually denoted as n) increases. Run-time efficiency is a topic of great interest in computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
: A program
Computer program
A computer program is a sequence of instructions written to perform a specified task with a computer. A computer requires programs to function, typically executing the program's instructions in a central processor. The program has an executable form that the computer can use directly to execute...
can take seconds, hours or even years to finish executing, depending on which algorithm it implements (see also performance analysis
Performance analysis
In software engineering, profiling is a form of dynamic program analysis that measures, for example, the usage of memory, the usage of particular instructions, or frequency and duration of function calls...
, which is the analysis of an algorithm's run-time in practice).
Shortcomings of empirical metrics
Since algorithms are platform-independent (i.e. a given algorithm can be implemented in an arbitrary programming languageProgramming language
A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
on an arbitrary computer
Computer
A computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...
running an arbitrary operating system
Operating system
An operating system is a set of programs that manage computer hardware resources and provide common services for application software. The operating system is the most important type of system software in a computer system...
), there are significant drawbacks to using an empirical
Empirical
The word empirical denotes information gained by means of observation or experimentation. Empirical data are data produced by an experiment or observation....
approach to gauge the comparative performance of a given set of algorithms.
Take as an example a program that looks up a specific entry in a sorted
Collation
Collation is the assembly of written information into a standard order. One common type of collation is called alphabetization, though collation is not limited to ordering letters of the alphabet...
list of size n. Suppose this program were implemented on Computer A, a state-of-the-art machine, using a linear search
Linear search
In computer science, linear search or sequential search is a method for finding a particular value in a list, that consists of checking every one of its elements, one at a time and in sequence, until the desired one is found....
algorithm, and on Computer B, a much slower machine, using a binary search algorithm. Benchmark testing
Benchmark (computing)
In computing, a benchmark is the act of running a computer program, a set of programs, or other operations, in order to assess the relative performance of an object, normally by running a number of standard tests and trials against it...
on the two computers running their respective programs might look something like the following:
| n (list size) | Computer A run-time (in nanosecond Nanosecond A nanosecond is one billionth of a second . One nanosecond is to one second as one second is to 31.7 years.The word nanosecond is formed by the prefix nano and the unit second. Its symbol is ns.... s) |
Computer B run-time (in nanosecond Nanosecond A nanosecond is one billionth of a second . One nanosecond is to one second as one second is to 31.7 years.The word nanosecond is formed by the prefix nano and the unit second. Its symbol is ns.... s) |
|---|---|---|
| 15 | 7 ns | 100,000 ns |
| 65 | 32 ns | 150,000 ns |
| 250 | 125 ns | 200,000 ns |
| 1,000 | 500 ns | 250,000 ns |
Based on these metrics, it would be easy to jump to the conclusion that Computer A is running an algorithm that is far superior in efficiency to that of Computer B. However, if the size of the input-list is increased to a sufficient number, that conclusion is dramatically demonstrated to be in error:
| n (list size) | Computer A run-time (in nanosecond Nanosecond A nanosecond is one billionth of a second . One nanosecond is to one second as one second is to 31.7 years.The word nanosecond is formed by the prefix nano and the unit second. Its symbol is ns.... s) |
Computer B run-time (in nanosecond Nanosecond A nanosecond is one billionth of a second . One nanosecond is to one second as one second is to 31.7 years.The word nanosecond is formed by the prefix nano and the unit second. Its symbol is ns.... s) |
|---|---|---|
| 15 | 7 ns | 100,000 ns |
| 65 | 32 ns | 150,000 ns |
| 250 | 125 ns | 200,000 ns |
| 1,000 | 500 ns | 250,000 ns |
| ... | ... | ... |
| 1,000,000 | 500,000 ns | 500,000 ns |
| 4,000,000 | 2,000,000 ns | 550,000 ns |
| 16,000,000 | 8,000,000 ns | 600,000 ns |
| ... | ... | ... |
| 63,072 × 1012 | 31,536 × 1012 ns, or 1 year |
1,375,000 ns, or 1.375 milliseconds |
Computer A, running the linear search program, exhibits a linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
growth rate. The program's run-time is directly proportional to its input size. Doubling the input size doubles the run time, quadrupling the input size quadruples the run-time, and so forth. On the other hand, Computer B, running the binary search program, exhibits a logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
ic growth rate. Doubling the input size only increases the run time by a constant amount (in this example, 25,000 ns). Even though Computer A is ostensibly a faster machine, Computer B will inevitably surpass Computer A in run-time because it's running an algorithm with a much slower growth rate.
Orders of growth
Informally, an algorithm can be said to exhibit a growth rate on the order of a mathematical functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
if beyond a certain input size n, the function f(n) times a positive constant provides an upper bound or limit
Asymptotic analysis
In mathematical analysis, asymptotic analysis is a method of describing limiting behavior. The methodology has applications across science. Examples are...
for the run-time of that algorithm. In other words, for a given input size n greater than some n0 and a constant c, the running time of that algorithm will never be larger than c × f(n). This concept is frequently expressed using Big O notation. For example, since the run-time of insertion sort
Insertion sort
Insertion sort is a simple sorting algorithm: a comparison sort in which the sorted array is built one entry at a time. It is much less efficient on large lists than more advanced algorithms such as quicksort, heapsort, or merge sort...
grows quadratically
Quadratic growth
In mathematics, a function or sequence is said to exhibit quadratic growth when its values are proportional to the square of the function argument or sequence position, in the limit as the argument or sequence position goes to infinity...
as its input size increases, insertion sort can be said to be of order O(n²).
Big O notation is a convenient way to express the worst-case scenario
Best, worst and average case
In computer science, best, worst and average cases of a given algorithm express what the resource usage is at least, at most and on average, respectively...
for a given algorithm, although it can also be used to express the average-case — for example, the worst-case scenario for quicksort is O(n²), but the average-case run-time is O(n log n).
Evaluating run-time complexity
The run-time complexity for the worst-case scenario of a given algorithm can sometimes be evaluated by examining the structure of the algorithm and making some simplifying assumptions. Consider the following pseudocodePseudocode
In computer science and numerical computation, pseudocode is a compact and informal high-level description of the operating principle of a computer program or other algorithm. It uses the structural conventions of a programming language, but is intended for human reading rather than machine reading...
:
1 get a positive integer from input
2 if n > 10
3 print "This might take a while..."
4 for i = 1 to n
5 for j = 1 to i
6 print i * j
7 print "Done!"
A given computer will take a discrete amount of time
DTIME
In computational complexity theory, DTIME is the computational resource of computation time for a deterministic Turing machine. It represents the amount of time that a "normal" physical computer would take to solve a certain computational problem using a certain algorithm...
to execute each of the instructions involved with carrying out this algorithm. The specific amount of time to carry out a given instruction will vary depending on which instruction is being executed and which computer is executing it, but on a conventional computer, this amount will be deterministic
Deterministic system (mathematics)
In mathematics, a deterministic system is a system in which no randomness is involved in the development of future states of the system. A deterministic model will thus always produce the same output from a given starting condition or initial state.-Examples:...
. Say that the actions carried out in step 1 are considered to consume time T1, step 2 uses time T2, and so forth.
In the algorithm above, steps 1, 2 and 7 will only be run once. For a worst-case evaluation, it should be assumed that step 3 will be run as well. Thus the total amount of time to run steps 1-3 and step 7 is:
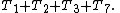
The loops in steps 4, 5 and 6 are trickier to evaluate. The outer loop test in step 4 will execute ( n + 1 )
times (note that an extra step is required to terminate the for loop, hence n + 1 and not n executions), which will consume T4( n + 1 ) time. The inner loop, on the other hand, is governed by the value of i, which iterates
Iteration
Iteration means the act of repeating a process usually with the aim of approaching a desired goal or target or result. Each repetition of the process is also called an "iteration," and the results of one iteration are used as the starting point for the next iteration.-Mathematics:Iteration in...
from 1 to n. On the first pass through the outer loop, j iterates from 1 to 1: The inner loop makes one pass, so running the inner loop body (step 6) consumes T6 time, and the inner loop test (step 5) consumes 2T5 time. During the next pass through the outer loop, j iterates from 1 to 2: the inner loop makes two passes, so running the inner loop body (step 6) consumes 2T6 time, and the inner loop test (step 5) consumes 3T5 time.
Altogether, the total time required to run the inner loop body can be expressed as an arithmetic progression
Arithmetic progression
In mathematics, an arithmetic progression or arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant...
:
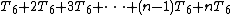
which can be factored
Factorization
In mathematics, factorization or factoring is the decomposition of an object into a product of other objects, or factors, which when multiplied together give the original...
as
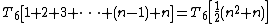
The total time required to run the inner loop test can be evaluated similarly:
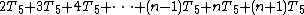
which can be factored as
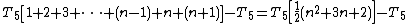
Therefore the total running time for this algorithm is:
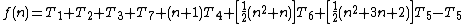
which reduces
Reduction (mathematics)
In mathematics, reduction refers to the rewriting of an expression into a simpler form. For example, the process of rewriting a fraction into one with the smallest whole-number denominator possible is called "reducing a fraction"...
to

As a rule-of-thumb, one can assume that the highest-order term in any given function dominates its rate of growth and thus defines its run-time order. In this example, n² is the highest-order term, so one can conclude that f(n) = O(n²). Formally this can be proven as follows:
Prove that
(for n ≥ 0)
Let k be a constant greater than or equal to [T1..T7]
(for n ≥ 1)
Thereforefor
A more elegant
Elegance
Elegance is a synonym for beauty that has come to acquire the additional connotations of unusual effectiveness and simplicity. It is frequently used as a standard of tastefulness particularly in the areas of visual design, decoration, the sciences, and the esthetics of mathematics...
approach to analyzing this algorithm would be to declare that [T1..T7] are all equal to one unit of time greater than or equal to [T1..T7]. This would mean that the algorithm's running time breaks down as follows:
(for n ≥ 1)
Growth rate analysis of other resources
The methodology of run-time analysis can also be utilized for predicting other growth rates, such as consumption of memory spaceDSPACE
In computational complexity theory, DSPACE or SPACE is the computational resource describing the resource of memory space for a deterministic Turing machine. It represents the total amount of memory space that a "normal" physical computer would need to solve a given computational problem with a...
. As an example, consider the following pseudocode which manages and reallocates memory usage by a program based on the size of a file
Computer file
A computer file is a block of arbitrary information, or resource for storing information, which is available to a computer program and is usually based on some kind of durable storage. A file is durable in the sense that it remains available for programs to use after the current program has finished...
which that program manages:
while (file still open)
let n = size of file
for every 100,000 kilobyte
Kilobyte
The kilobyte is a multiple of the unit byte for digital information. Although the prefix kilo- means 1000, the term kilobyte and symbol KB have historically been used to refer to either 1024 bytes or 1000 bytes, dependent upon context, in the fields of computer science and information...
s of increase in file size
double the amount of memory reserved
In this instance, as the file size n increases, memory will be consumed at an exponential growth
Exponential growth
Exponential growth occurs when the growth rate of a mathematical function is proportional to the function's current value...
rate, which is order O(2n).
Relevance
Algorithm analysis is important in practice because the accidental or unintentional use of an inefficient algorithm can significantly impact system performance. In time-sensitive applications, an algorithm taking too long to run can render its results outdated or useless. An inefficient algorithm can also end up requiring an uneconomical amount of computing power or storage in order to run, again rendering it practically useless.See also
- Amortized analysisAmortized analysisIn computer science, amortized analysis is a method of analyzing algorithms that considers the entire sequence of operations of the program. It allows for the establishment of a worst-case bound for the performance of an algorithm irrespective of the inputs by looking at all of the operations...
- Asymptotic analysisAsymptotic analysisIn mathematical analysis, asymptotic analysis is a method of describing limiting behavior. The methodology has applications across science. Examples are...
- Best, worst and average caseBest, worst and average caseIn computer science, best, worst and average cases of a given algorithm express what the resource usage is at least, at most and on average, respectively...
- Big O notationBig O notationIn mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
- Computational complexity theoryComputational complexity theoryComputational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
- NP-CompleteNP-completeIn computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
- Numerical analysisNumerical analysisNumerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
- Polynomial time
- Program optimization
- Profiling (computer programming)
- Smoothed analysisSmoothed analysisSmoothed analysis is a way of measuring the complexity of an algorithm. It gives a more realistic analysis of the practical performance of the algorithm, such as its running time, than using worst-case or average-case scenarios....
- Time complexityTime complexityIn computer science, the time complexity of an algorithm quantifies the amount of time taken by an algorithm to run as a function of the size of the input to the problem. The time complexity of an algorithm is commonly expressed using big O notation, which suppresses multiplicative constants and...
— includes table of orders for common algorithms