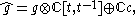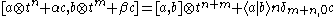Affine Lie algebra
Encyclopedia
In mathematics
, an affine Lie algebra is an infinite-dimensional Lie algebra
that is constructed in a canonical fashion out of a finite-dimensional simple Lie algebra. It is a Kac–Moody algebra
for which the generalized Cartan matrix is positive semi-definite and has corank 1. From purely mathematical point of view, affine Lie algebras are interesting because their representation theory
, like representation theory of finite dimensional, semisimple Lie algebras is much better understood than that of general Kac–Moody algebras. As observed by Victor Kac
, the character formula for representations of affine Lie algebras implies certain combinatorial identities, the Macdonald identities.
Affine Lie algebras play an important role in string theory
and conformal field theory
due to the way they are constructed: starting from a simple Lie algebra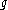 , one considers the loop algebra,
, one considers the loop algebra, 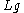 , formed by the
, formed by the 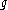 -valued functions on a circle (interpreted as the closed string) with pointwise commutator. The affine Lie algebra
-valued functions on a circle (interpreted as the closed string) with pointwise commutator. The affine Lie algebra 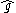 is obtained by adding one extra dimension to the loop algebra and modifying a commutator in a non-trivial way, which physicists call a quantum anomaly
is obtained by adding one extra dimension to the loop algebra and modifying a commutator in a non-trivial way, which physicists call a quantum anomaly
and mathematicians a central extension
. More generally,
if σ is an automorphism
of the simple Lie algebra associated to an automorphism of its Dynkin diagram, the twisted loop algebra
associated to an automorphism of its Dynkin diagram, the twisted loop algebra 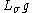 consists of
consists of 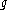 -valued functions f on the real line which satisfy
-valued functions f on the real line which satisfy
the twisted periodicity condition f(x+2π) = σ f(x). Their central extensions are precisely the twisted affine Lie algebras. The point of view of string theory helps to understand many deep properties of affine Lie algebras, such as the fact that the characters of their representations transform amongst themselves under the modular group
.
 is a finite dimensional simple Lie algebra, the corresponding
is a finite dimensional simple Lie algebra, the corresponding
affine Lie algebra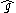 is constructed as a central extension of the infinite-dimensional Lie algebra
is constructed as a central extension of the infinite-dimensional Lie algebra 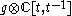 , with one-dimensional center
, with one-dimensional center 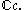
As a vector space,
where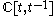 is the complex vector space of Laurent polynomials
is the complex vector space of Laurent polynomials
in the indeterminate t. The Lie bracket is defined by the formula
for all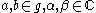 and
and 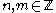 , where
, where  is the Lie bracket in the Lie algebra
is the Lie bracket in the Lie algebra 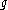 and
and 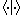 is the Cartan-Killing form
is the Cartan-Killing form
on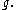
The affine Lie algebra corresponding to a finite-dimensional semisimple Lie algebra is the direct sum of the affine Lie algebras corresponding to its simple summands. There is a distinguished derivation of the affine Lie algebra defined by
The corresponding affine Kac-Moody algebra is defined by adding an extra generator d satisfying [d,A] = δ(A) (a semidirect product
).
of the Lie algebra. In particular, this group always contains the identity element, and the corresponding affine Lie algebra is called an untwisted affine Lie algebra. When the simple algebra admits automorphisms that are not inner automorphisms, one may obtain other Dynkin diagrams and these correspond to twisted affine Lie algebras.
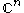 . In this case one also needs to add n further central elements for the n abelian generators.
. In this case one also needs to add n further central elements for the n abelian generators.
The second integral cohomology of the loop group of the corresponding simple compact Lie group is isomorphic to the integers. Central extensions of the affine Lie group by a single generator are topologically circle bundles over this free loop group, which are classified by a two-class known as the first Chern class
of the fibration
. Therefore the central extensions of an affine Lie group are classified by a single parameter k which is called the level in the physics literature, where it first appeared. Unitary highest weight representations of the affine compact groups only exist when k is a natural number. More generally, if one considers a semi-simple algebra, there is a central charge for each simple component.
(for example, in conformal field theories
such as the WZW model and coset models and even on the worldsheet of the heterotic string
), geometry, and elsewhere in mathematics.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an affine Lie algebra is an infinite-dimensional Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
that is constructed in a canonical fashion out of a finite-dimensional simple Lie algebra. It is a Kac–Moody algebra
Kac–Moody algebra
In mathematics, a Kac–Moody algebra is a Lie algebra, usually infinite-dimensional, that can be defined by generators and relations through a generalized Cartan matrix...
for which the generalized Cartan matrix is positive semi-definite and has corank 1. From purely mathematical point of view, affine Lie algebras are interesting because their representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
, like representation theory of finite dimensional, semisimple Lie algebras is much better understood than that of general Kac–Moody algebras. As observed by Victor Kac
Victor Kac
Victor G. Kac is a Soviet and American mathematician at MIT, known for his work in representation theory. He discovered Kac–Moody algebras, and used the Weyl–Kac character formula for them to reprove the Macdonald identities...
, the character formula for representations of affine Lie algebras implies certain combinatorial identities, the Macdonald identities.
Affine Lie algebras play an important role in string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
and conformal field theory
Conformal field theory
A conformal field theory is a quantum field theory that is invariant under conformal transformations...
due to the way they are constructed: starting from a simple Lie algebra
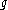 , one considers the loop algebra,
, one considers the loop algebra, 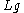 , formed by the
, formed by the 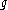 -valued functions on a circle (interpreted as the closed string) with pointwise commutator. The affine Lie algebra
-valued functions on a circle (interpreted as the closed string) with pointwise commutator. The affine Lie algebra 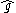 is obtained by adding one extra dimension to the loop algebra and modifying a commutator in a non-trivial way, which physicists call a quantum anomaly
is obtained by adding one extra dimension to the loop algebra and modifying a commutator in a non-trivial way, which physicists call a quantum anomalyAnomaly (physics)
In quantum physics an anomaly or quantum anomaly is the failure of a symmetry of a theory's classical action to be a symmetry of any regularization of the full quantum theory. In classical physics an anomaly is the failure of a symmetry to be restored in the limit in which the symmetry-breaking...
and mathematicians a central extension
Central extension
Central extension may refer to:* Central Extension , a rail line* Central extension , a type of group extension...
. More generally,
if σ is an automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
of the simple Lie algebra
 associated to an automorphism of its Dynkin diagram, the twisted loop algebra
associated to an automorphism of its Dynkin diagram, the twisted loop algebra 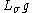 consists of
consists of 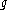 -valued functions f on the real line which satisfy
-valued functions f on the real line which satisfythe twisted periodicity condition f(x+2π) = σ f(x). Their central extensions are precisely the twisted affine Lie algebras. The point of view of string theory helps to understand many deep properties of affine Lie algebras, such as the fact that the characters of their representations transform amongst themselves under the modular group
Modular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
.
Definition
If is a finite dimensional simple Lie algebra, the corresponding
is a finite dimensional simple Lie algebra, the correspondingaffine Lie algebra
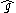 is constructed as a central extension of the infinite-dimensional Lie algebra
is constructed as a central extension of the infinite-dimensional Lie algebra 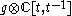 , with one-dimensional center
, with one-dimensional center 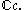
As a vector space,
where
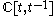 is the complex vector space of Laurent polynomials
is the complex vector space of Laurent polynomialsLaurent series
In mathematics, the Laurent series of a complex function f is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where...
in the indeterminate t. The Lie bracket is defined by the formula
for all
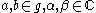 and
and 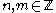 , where
, where  is the Lie bracket in the Lie algebra
is the Lie bracket in the Lie algebra 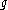 and
and 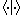 is the Cartan-Killing form
is the Cartan-Killing formKilling form
In mathematics, the Killing form, named after Wilhelm Killing, is a symmetric bilinear form that plays a basic role in the theories of Lie groups and Lie algebras...
on
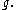
The affine Lie algebra corresponding to a finite-dimensional semisimple Lie algebra is the direct sum of the affine Lie algebras corresponding to its simple summands. There is a distinguished derivation of the affine Lie algebra defined by
The corresponding affine Kac-Moody algebra is defined by adding an extra generator d satisfying [d,A] = δ(A) (a semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
).
Constructing the Dynkin diagrams
The Dynkin diagram of each affine Lie algebra consists of that of the corresponding simple Lie algebra plus an additional node, which corresponds to the addition of an imaginary root. Of course, such a node cannot be attached to the Dynkin diagram in just any location, but for each simple Lie algebra there exists a number of possible attachments equal to the cardinality of the group of outer automorphismsOuter automorphism group
In mathematics, the outer automorphism group of a group Gis the quotient Aut / Inn, where Aut is the automorphism group of G and Inn is the subgroup consisting of inner automorphisms. The outer automorphism group is usually denoted Out...
of the Lie algebra. In particular, this group always contains the identity element, and the corresponding affine Lie algebra is called an untwisted affine Lie algebra. When the simple algebra admits automorphisms that are not inner automorphisms, one may obtain other Dynkin diagrams and these correspond to twisted affine Lie algebras.
The set of extended (untwisted) affine Dynkin diagrams, with added nodes in green |
"Twisted" affine forms are named with (2) or (3) superscripts. (k is the number of nodes in the graph) |
Classifying the central extensions
The attachment of an extra node to the Dynkin diagram of the corresponding simple Lie algebra corresponds to the following construction. An affine Lie algebra can always be constructed as a central extension of the loop algebra of the corresponding simple Lie algebra. If one wishes to begin instead with a semisimple Lie algebra, then one needs to centrally extend by a number of elements equal to the number of simple components of the semisimple algebra. In physics, one often considers instead the direct sum of a semisimple algebra and an abelian algebra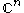 . In this case one also needs to add n further central elements for the n abelian generators.
. In this case one also needs to add n further central elements for the n abelian generators.The second integral cohomology of the loop group of the corresponding simple compact Lie group is isomorphic to the integers. Central extensions of the affine Lie group by a single generator are topologically circle bundles over this free loop group, which are classified by a two-class known as the first Chern class
Chern class
In mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
of the fibration
Fibration
In topology, a branch of mathematics, a fibration is a generalization of the notion of a fiber bundle. A fiber bundle makes precise the idea of one topological space being "parameterized" by another topological space . A fibration is like a fiber bundle, except that the fibers need not be the same...
. Therefore the central extensions of an affine Lie group are classified by a single parameter k which is called the level in the physics literature, where it first appeared. Unitary highest weight representations of the affine compact groups only exist when k is a natural number. More generally, if one considers a semi-simple algebra, there is a central charge for each simple component.
Applications
They appear naturally in theoretical physicsTheoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
(for example, in conformal field theories
Conformal field theory
A conformal field theory is a quantum field theory that is invariant under conformal transformations...
such as the WZW model and coset models and even on the worldsheet of the heterotic string
Heterotic string
In physics, a heterotic string is a peculiar mixture of the bosonic string and the superstring...
), geometry, and elsewhere in mathematics.