Killing form
Encyclopedia
In mathematics
, the Killing form, named after Wilhelm Killing
, is a symmetric bilinear form
that plays a basic role in the theories of Lie group
s and Lie algebra
s. The Killing form was essentially introduced into Lie algebra theory by in his thesis; although Killing had previously made a passing mention of it he made no serious use of it.
g over a field
K. Every element x of g defines the adjoint endomorphism
ad(x) (also written as adx) of g with the help of the Lie bracket, as
Now, supposing g is of finite dimension, the trace of the composition of two such endomorphisms defines a symmetric bilinear form
with values in K, the Killing form on g.
where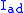
is the Dynkin index of the adjoint representation of g.
Here
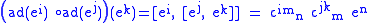
in Einstein summation notation
and so we can write
where the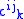
are the structure coefficients of the Lie algebra. The Killing form is the simplest 2-tensor
that can be formed from the structure constants.
In the above indexed definition, we are careful to distinguish upper and lower indexes (co- and contra-variant indexes). This is because, in many cases, the Killing form can be used as a metric tensor on a manifold, in which case the distinction becomes an important one for the transformation properties of tensors. When the Lie algebra is semisimple, its Killing form is nondegenerate, and hence can be used as a metric tensor
to raise and lower indexes. In this case, it is always possible to choose a basis for g such that the structure constants with all upper indexes are completely antisymmetric.
, the number of positive entries is an invariant of the bilinear form, i.e. it does not depend on the choice of the diagonalizing basis, and is called the index of the Lie algebra g. This is a number between 0 and the dimension of g which is an important invariant of the real Lie algebra. In particular, a real Lie algebra g is called compact if the Killing form is negative definite. It is known that under the Lie correspondence, compact Lie algebra
s correspond to compact Lie groups.
If gC is a semisimple Lie algebra over the complex numbers, then there are several non-isomorphic real Lie algebras whose complexification
is gC, which are called its real forms. It turns out that every complex semisimple Lie algebra admits a unique (up to isomorphism) compact real form g. The real forms of a given complex semisimple Lie algebra are frequently labeled by the positive index of inertia of their Killing form.
For example, the complex special linear algebra
sl(2,C) has two real forms, the real special linear algebra, denoted sl(2,R), and the special unitary algebra
, denoted su(2). The first one is noncompact, the so-called split real form, and its Killing form has signature (2,1). The second one is the compact real form and its Killing form is negative definite, i.e. has signature (0,3). The corresponding Lie groups are the noncompact group SL(2,R) of 2 by 2 real matrices with the unit determinant and the special unitary group SU(2), which is compact.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Killing form, named after Wilhelm Killing
Wilhelm Killing
Wilhelm Karl Joseph Killing was a German mathematician who made important contributions to the theories of Lie algebras, Lie groups, and non-Euclidean geometry....
, is a symmetric bilinear form
Symmetric bilinear form
A symmetric bilinear form is a bilinear form on a vector space that is symmetric. Symmetric bilinear forms are of great importance in the study of orthogonal polarity and quadrics....
that plays a basic role in the theories of Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s and Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s. The Killing form was essentially introduced into Lie algebra theory by in his thesis; although Killing had previously made a passing mention of it he made no serious use of it.
Definition
Consider a Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
g over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K. Every element x of g defines the adjoint endomorphism
Adjoint endomorphism
In mathematics, the adjoint endomorphism or adjoint action is an endomorphism of Lie algebras that plays a fundamental role in the development of the theory of Lie algebras and Lie groups....
ad(x) (also written as adx) of g with the help of the Lie bracket, as
Now, supposing g is of finite dimension, the trace of the composition of two such endomorphisms defines a symmetric bilinear form
Symmetric bilinear form
A symmetric bilinear form is a bilinear form on a vector space that is symmetric. Symmetric bilinear forms are of great importance in the study of orthogonal polarity and quadrics....
- B(x, y) = trace(ad(x)ad(y)),
with values in K, the Killing form on g.
Properties
- The Killing form B is bilinear and symmetric.
- The Killing form is an invariant form, in the sense that it has the 'associativity' property
-
- B([x,y],z)=B(x,[y,z]),
- where [,] is the Lie bracketLie bracketLie bracket can refer to:*A bilinear binary operation defined on elements of a Lie algebra*Lie bracket of vector fields...
.
- If g is a simple Lie algebra then any invariant symmetric bilinear form on g is a scalar multiple of the Killing form.
- The Killing form is also invariant under automorphismAutomorphismIn mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
s s of the algebra g, that is,
-
- B(s(x),s(y)) = B(x,y)
- for s in Aut(g).
- The Cartan criterion states that a Lie algebra is semisimple if and only if the Killing form is non-degenerateDegenerate formIn mathematics, specifically linear algebra, a degenerate bilinear form ƒ on a vector space V is one such that the map from V to V^* given by v \mapsto is not an isomorphism...
.
- The Killing form of a nilpotent Lie algebra is identically zero.
- If I and J are two ideals in a Lie algebra g with zero intersection, then I and J are orthogonal subspaces with respect to the Killing form.
- If a given Lie algebra g is a direct sum of its ideals I1,...,In, then the Killing form of g is the direct sum of the Killing forms of the individual summands.
Matrix elements
Given a basis ei of the Lie algebra g, the matrix elements of the Killing form are given bywhere
is the Dynkin index of the adjoint representation of g.Here
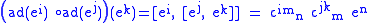
in Einstein summation notation
and so we can write
where the
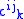are the structure coefficients of the Lie algebra. The Killing form is the simplest 2-tensorTensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
that can be formed from the structure constants.
In the above indexed definition, we are careful to distinguish upper and lower indexes (co- and contra-variant indexes). This is because, in many cases, the Killing form can be used as a metric tensor on a manifold, in which case the distinction becomes an important one for the transformation properties of tensors. When the Lie algebra is semisimple, its Killing form is nondegenerate, and hence can be used as a metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
to raise and lower indexes. In this case, it is always possible to choose a basis for g such that the structure constants with all upper indexes are completely antisymmetric.
Connection with real forms
Suppose that g is a semisimple Lie algebra over the field of real numbers. By Cartan's criterion, the Killing form is nondegenerate, and can be diagonalized in a suitable basis with the diagonal entries +1 or -1. By Sylvester's law of inertiaSylvester's law of inertia
Sylvester's law of inertia is a theorem in matrix algebra about certain properties of the coefficient matrix of a real quadratic form that remain invariant under a change of coordinates...
, the number of positive entries is an invariant of the bilinear form, i.e. it does not depend on the choice of the diagonalizing basis, and is called the index of the Lie algebra g. This is a number between 0 and the dimension of g which is an important invariant of the real Lie algebra. In particular, a real Lie algebra g is called compact if the Killing form is negative definite. It is known that under the Lie correspondence, compact Lie algebra
Compact Lie algebra
In the mathematical field of Lie theory, a Lie algebra is compact if it is the Lie algebra of a compact Lie group. Intrinsically, a compact Lie algebra is a real Lie algebra whose Killing form is negative definite, though this definition does not quite agree with the previous...
s correspond to compact Lie groups.
If gC is a semisimple Lie algebra over the complex numbers, then there are several non-isomorphic real Lie algebras whose complexification
Complexification
In mathematics, the complexification of a real vector space V is a vector space VC over the complex number field obtained by formally extending scalar multiplication to include multiplication by complex numbers. Any basis for V over the real numbers serves as a basis for VC over the complex...
is gC, which are called its real forms. It turns out that every complex semisimple Lie algebra admits a unique (up to isomorphism) compact real form g. The real forms of a given complex semisimple Lie algebra are frequently labeled by the positive index of inertia of their Killing form.
For example, the complex special linear algebra
Special linear group
In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
sl(2,C) has two real forms, the real special linear algebra, denoted sl(2,R), and the special unitary algebra
Special unitary group
The special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...
, denoted su(2). The first one is noncompact, the so-called split real form, and its Killing form has signature (2,1). The second one is the compact real form and its Killing form is negative definite, i.e. has signature (0,3). The corresponding Lie groups are the noncompact group SL(2,R) of 2 by 2 real matrices with the unit determinant and the special unitary group SU(2), which is compact.