
Triangle center
Encyclopedia
In geometry
a triangle center (or triangle centre) is a point in the plane that is in some sense a center of a triangle akin to the centers of squares
and circle
s. For example the centroid
, circumcenter, incenter and orthocenter were familiar to the ancient Greeks, and can be obtained by simple constructions. Each of them has the property that it is invariant
under similarity
. In other words it will always occupy the same position (relative to the vertices) under the operations of rotation
, reflection
, and dilation. Consequently this invariance is a necessary property for any point aspiring to be a triangle center. It rules out various well-known points such as the Brocard point
s, named after Henri Brocard
(1845–1922), which are not invariant under reflection and so fail to qualify as triangle centers.
, nine-point center, symmedian point, Gergonne point, and Feuerbach point were discovered. During the revival of interest in triangle geometry in the 1980s it was noticed that these special points share some general properties that now form the basis for a formal definition of triangle center. Clark Kimberling's Encyclopedia of Triangle Centers
contains an annotated list of 3587 triangle centers.
Each of these centers is assigned a unique name. In cases where no particular name arises from geometrical or historical considerations, the name of a star is used instead. For example the 770th point in the list, is named point Acamar.
f of three real variables a, b, c may have the following properties :-
If a non-zero f has both these properties it is called a triangle center function. If f is a triangle center function and a, b, c are the side-lengths of a reference triangle then the point whose trilinear coordinates
are f(a,b,c) : f(b,c,a) : f(c,a,b) is called a triangle center.
This definition ensures that triangle centers of similar triangles meet the invariance criteria specified above. By convention only the first of the three trilinear coordinates of a triangle center is quoted since the other two are obtained by cyclic permutation
of a, b, c. This process is known as cyclicity.
Every triangle center function corresponds to a unique triangle center. This correspondence is not bijective. Different functions may define the same triangle center. For example the functions f1(a,b,c) = 1/a and f2(a,b,c) = bc both correspond to the centroid.
Two triangle center functions define the same triangle center if and only if their ratio is a function symmetric in a, b and c.
Even if a triangle center function is well-defined everywhere the same cannot always be said for its associated triangle center. For example let f(a, b, c) be 0 if a/b and a/c are both rational and 1 otherwise. Then for any triangle with integer sides the associated triangle center evaluates to 0:0:0 which is undefined.
is restricted to the region of ℝ3 where a ≤ b + c, b ≤ c + a, and c ≤ a + b. This region T is the domain of all triangles, and it is the default domain for all triangle-based functions.
triangles.

Let f(a,b,c) = a(b2 + c2 − a2). Then
so f is a triangle center function. Since the corresponding triangle center has the same trilinears as the circumcenter it follows that the circumcenter is a triangle center.
Expressing these coordinates in terms of a, b and c, one can verify that they indeed satisfy the defining properties of the coordinates of a triangle center. Hence the 1st isogonic center is also a triangle center.
Then f is bisymmetric and homogeneous so it is a triangle center function. Moreover the corresponding triangle center coincides with the obtuse angled vertex whenever any vertex angle exceeds 2π/3, and with the 1st isogonic center otherwise. Therefore this triangle center is none other than the Fermat point.
The first and second Brocard points are one of many Bicentric Pairs of Points. Several binary operations, such as midpoint and trilinear product, when applied to the two Brocard points, as well as other bicentric pairs, produce triangle centers.
(*) : actually the 1st isogonic center, but also the Fermat point whenever A,B,C ≤ 2π/3
Also for each center only the first trilinear coordinate f(a,b,c) is specified. The other coordinates can be easily derived using the cyclicity property of trilinear coordinates.
so two components of the associated triangle center are always equal. Therefore all triangle centers of an isosceles triangle must lie on its line of symmetry. For an equilateral triangle all three components are equal so all centers coincide with the centroid. So, like a circle, an equilateral triangle has a unique center.
This is readily seen to be a triangle center function and (provided the triangle is scalene) the corresponding triangle center is the excenter opposite to the largest vertex angle. The other two excenters can be picked out by similar functions. However as indicated above only one of the excenters of an isosceles triangle and none of the excenters of an equilateral triangle can ever be a triangle center.
under addition, subtraction, and multiplication. This gives an easy way to create new triangle centers. However distinct normalized triangle center functions will often define the same triangle center, for example f and (abc)−1(a+b+c)3f .
Then f is a triangle center function and α : β : γ is the corresponding triangle center whenever the sides of the reference triangle are labelled so that a < b < c. Thus every point is potentially a triangle center. However the vast majority of triangle centers are of little interest, just as most continuous functions are of little interest. The Encyclopedia of Triangle Centers
is an ever-expanding list of interesting ones.
For the corresponding triangle center there are four distinct possibilities :-
Routine calculation shows that in every case these trilinears represent the incenter of the tangential triangle. So this point is a triangle center that is a close companion of the circumcenter.
, isotropic scaling
, homothety, and homothecy.
, but triangle centers can also be studied in hyperbolic geometry
. Using gyrotrigonometry, trigonometric barycentric coordinates can be calculated that will coincide for euclidean and hyperbolic geometry. In order for the coordinates to coincide, the expressions must not encapsulate the specification of the anglesum being 180 degrees.
s or higher-dimensional simplices
.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
a triangle center (or triangle centre) is a point in the plane that is in some sense a center of a triangle akin to the centers of squares
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
and circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
s. For example the centroid
Centroid
In geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...
, circumcenter, incenter and orthocenter were familiar to the ancient Greeks, and can be obtained by simple constructions. Each of them has the property that it is invariant
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
under similarity
Similarity (geometry)
Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
. In other words it will always occupy the same position (relative to the vertices) under the operations of rotation
Rotation (mathematics)
In geometry and linear algebra, a rotation is a transformation in a plane or in space that describes the motion of a rigid body around a fixed point. A rotation is different from a translation, which has no fixed points, and from a reflection, which "flips" the bodies it is transforming...
, reflection
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
, and dilation. Consequently this invariance is a necessary property for any point aspiring to be a triangle center. It rules out various well-known points such as the Brocard point
Brocard point
In geometry, Brocard points are special points within a triangle. They are named after Henri Brocard , a French mathematician.-Definition:...
s, named after Henri Brocard
Henri Brocard
Pierre René Jean Baptiste Henri Brocard was a French meteorologist and mathematician, in particular a geometer...
(1845–1922), which are not invariant under reflection and so fail to qualify as triangle centers.
History
Even though the ancient Greeks discovered the classic centers of a triangle they had not formulated any definition of a triangle center. After the ancient Greeks, several special points associated with a triangle like Fermat pointFermat point
In geometry the Fermat point of a triangle, also called Torricelli point, is a point such that the total distance from the three vertices of the triangle to the point is the minimum possible...
, nine-point center, symmedian point, Gergonne point, and Feuerbach point were discovered. During the revival of interest in triangle geometry in the 1980s it was noticed that these special points share some general properties that now form the basis for a formal definition of triangle center. Clark Kimberling's Encyclopedia of Triangle Centers
Encyclopedia of Triangle Centers
The Encyclopedia of Triangle Centers is an on-line list of more than 3,000 points or "centers" associated with the geometry of a triangle. It is maintained by Clark Kimberling, Professor of Mathematics at the University of Evansville....
contains an annotated list of 3587 triangle centers.
Each of these centers is assigned a unique name. In cases where no particular name arises from geometrical or historical considerations, the name of a star is used instead. For example the 770th point in the list, is named point Acamar.
Formal definition
A real-valued functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
f of three real variables a, b, c may have the following properties :-
- Homogeneity: f(ta,tb,tc) = tn f(a,b,c) for some constant n and for all t > 0.
- Bisymmetry in the second and third variables: f(a,b,c) = f(a,c,b).
If a non-zero f has both these properties it is called a triangle center function. If f is a triangle center function and a, b, c are the side-lengths of a reference triangle then the point whose trilinear coordinates
Trilinear coordinates
In geometry, the trilinear coordinates of a point relative to a given triangle describe the relative distances from the three sides of the triangle. Trilinear coordinates are an example of homogeneous coordinates...
are f(a,b,c) : f(b,c,a) : f(c,a,b) is called a triangle center.
This definition ensures that triangle centers of similar triangles meet the invariance criteria specified above. By convention only the first of the three trilinear coordinates of a triangle center is quoted since the other two are obtained by cyclic permutation
Cyclic permutation
A cyclic permutation or circular permutation is a permutation built from one or more sets of elements in cyclic order.The notion "cyclic permutation" is used in different, but related ways:- Definition 1 :right|mapping of permutation...
of a, b, c. This process is known as cyclicity.
Every triangle center function corresponds to a unique triangle center. This correspondence is not bijective. Different functions may define the same triangle center. For example the functions f1(a,b,c) = 1/a and f2(a,b,c) = bc both correspond to the centroid.
Two triangle center functions define the same triangle center if and only if their ratio is a function symmetric in a, b and c.
Even if a triangle center function is well-defined everywhere the same cannot always be said for its associated triangle center. For example let f(a, b, c) be 0 if a/b and a/c are both rational and 1 otherwise. Then for any triangle with integer sides the associated triangle center evaluates to 0:0:0 which is undefined.
Default domain
In some cases these functions are not defined on the whole of ℝ3. For example the trilinears of X365 are a1/2 : b1/2 : c1/2 so a, b, c cannot be negative. Furthermore in order to represent the sides of a triangle they must satisfy the triangle inequality. So, in practice, every function's domainDomain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
is restricted to the region of ℝ3 where a ≤ b + c, b ≤ c + a, and c ≤ a + b. This region T is the domain of all triangles, and it is the default domain for all triangle-based functions.
Other useful domains
There are various instances where it may be desirable to restrict the analysis to a smaller domain than T. For example :-- The centers X3, X4, X22, X24, X40 make specific reference to acuteTriangleA triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
triangles,
namely that region of T where a2 ≤ b2 + c2, b2 ≤ c2 + a2, c2 ≤ a2 + b2. - When differentiating between the Fermat point and X13 the domain of triangles with an angle exceeding 2π/3 is important,
in other words triangles for which a2 > b2 + bc + c2 or b2 > c2 + ca + a2 or c2 > a2 + ab + b2. - A domain of much practical value since it is dense in T yet excludes all trivial triangles (ie points) and degenerate triangles
(ie lines) is the set of all scaleneTriangleA triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
triangles. It is obtained by removing the planes b = c, c = a, a = b from T.
Domain symmetry
Not every subset D ⊆ T is a viable domain. In order to support the bisymmetry test D must be symmetric about the planes b = c, c = a, a = b. To support cyclicity it must also be invariant under 2π/3 rotations about the line a = b = c. The simplest domain of all is the line (t,t,t) which corresponds to the set of all equilateralTriangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
triangles.
Examples

Circumcenter
The point of concurrence of the perpendicular bisectors of the sides of triangle ABC is the circumcenter. The trilinear coordinates of the circumcenter are- a(b2 + c2 − a2) : b(c2 + a2 − b2) : c(a2 + b2 − c2).
Let f(a,b,c) = a(b2 + c2 − a2). Then
- f(ta,tb,tc) = (ta) ( (tb)2 + (tc)2 − (ta)2 ) = t3 ( a( b2 + c2 − a2) ) = t3 f(a,b,c) (homogeneity)
- f(a,c,b) = a(c2 + b2 − a2) = a(b2 + c2 − a2) = f(a,b,c) (bisymmetry)
so f is a triangle center function. Since the corresponding triangle center has the same trilinears as the circumcenter it follows that the circumcenter is a triangle center.
1st isogonic center
Let A'BC be the equilateral triangle having base BC and vertex A' on the negative side of BC and let AB'C and ABC' be similarly constructed equilateral triangles based on the other two sides of triangle ABC. Then the lines AA', BB' and CC' are concurrent and the point of concurrence is the 1st isogonic center. Its trilinear coordinates are- csc(A + π/3) : csc(B + π/3) : csc(C + π/3).
Expressing these coordinates in terms of a, b and c, one can verify that they indeed satisfy the defining properties of the coordinates of a triangle center. Hence the 1st isogonic center is also a triangle center.
Fermat point
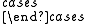 |
1 | if a2 > b2 + bc + c2 | (equivalently A > 2π/3) | |
| Let f(a,b,c) = | 0 | if b2 > c2 + ca + a2 or c2 > a2 + ab + b2 | (equivalently B > 2π/3 or C > 2π/3) | |
| csc(A + π/3) | otherwise | (equivalently no vertex angle exceeds 2π/3). |
Then f is bisymmetric and homogeneous so it is a triangle center function. Moreover the corresponding triangle center coincides with the obtuse angled vertex whenever any vertex angle exceeds 2π/3, and with the 1st isogonic center otherwise. Therefore this triangle center is none other than the Fermat point.
Brocard points
The trilinear coordinates of the first Brocard point are c/b : a/c : b/a. These coordinates satisfy the properties of homogeneity and cyclicity but not bisymmetry. So the first Brocard point is not (in general) a triangle center. The second Brocard point has trilinear coordinates b/c : c/a : a/b and similar remarks apply. However in an equilateral triangle the Brocard points coincide with the centroid and are therefore a triangle center when the domain of triangle centers is restricted to equilateral triangles. Analogously, the functions e^x and cos(x) coincide when restricted to the domain {0}.The first and second Brocard points are one of many Bicentric Pairs of Points. Several binary operations, such as midpoint and trilinear product, when applied to the two Brocard points, as well as other bicentric pairs, produce triangle centers.
Classical triangle centers
| Position in Encyclopedia of Triangle Centers |
Name | Notation | Trilinear coordinates |
|---|---|---|---|
| X1 | Incenter | I | 1 : 1 : 1 |
| X2 | Centroid | G | bc : ca : ab |
| X3 | Circumcenter | O | cos A : cos B : cos C |
| X4 | Orthocenter | H | sec A : sec B : sec C |
| X5 | Nine-point center | N | cos(B − C) : cos(C − A) : cos(A − B) |
| X6 | Symmedian point | K | a : b : c |
| X7 | Gergonne point | Ge | bc/(b + c − a) : ca/(c + a − b) : ab/(a + b − c) |
| X8 | Nagel point Nagel point In geometry, the Nagel point is a point associated with any triangle. Given a triangle ABC, let TA, TB, and TC be the extouch points in which the A-excircle meets line BC, the B-excircle meets line CA, and C-excircle meets line AB, respectively... |
Na | (b + c − a)/a : (c + a − b)/b: (a + b − c)/c |
| X9 | Mittenpunkt Mittenpunkt In geometry, the mittenpunkt of a triangle is a triangle center: a point defined from the triangle that is invariant under Euclidean transformations of the triangle. It is defined as the symmedian point of the excentral triangle of the given triangle. It is also the centroid of the Mandart... |
M | b + c − a : c + a − b : a + b − c |
| X10 | Spieker center | Sp | bc(b + c) : ca(c + a) : ab(a + b) |
| X11 | Feuerbach point | F | 1 − cos(B − C) : 1 − cos(C − A) : 1 − cos(A − B) |
| X13 | Fermat point Fermat point In geometry the Fermat point of a triangle, also called Torricelli point, is a point such that the total distance from the three vertices of the triangle to the point is the minimum possible... |
X | csc(A + π/3) : csc(B + π/3) : csc(C + π/3) * |
| X15 X16 |
Isodynamic points | S S′ |
sin(A + π/3) : sin(B + π/3) : sin(C + π/3) sin(A − π/3) : sin(B − π/3) : sin(C − π/3) |
| X17 X18 |
Napoleon points | N N′ |
sec(A − π/3) : sec(B − π/3) : sec(C − π/3) sec(A + π/3) : sec(B + π/3) : sec(C + π/3) |
| X99 | Steiner point | S | bc/(b2 − c2) : ca/(c2 − a2) : ab/(a2 − b2) |
(*) : actually the 1st isogonic center, but also the Fermat point whenever A,B,C ≤ 2π/3
Recent triangle centers
In the following table of recent triangle centers, no specific notations are mentioned for the various points.Also for each center only the first trilinear coordinate f(a,b,c) is specified. The other coordinates can be easily derived using the cyclicity property of trilinear coordinates.
| Position in Encyclopedia of Triangle Centers |
Name | Center function f(a,b,c) |
|---|---|---|
| X21 | Schiffler point | 1/(cos B + cos C) |
| X22 | Exeter point | a(b4 + c4 − a4) |
| X111 | Parry point | a/(2a2 − b2 − c2) |
| X173 | Congruent isoscelizers point | tan(A/2) + sec(A/2) |
| X174 | Yff center of congruence | sec(A/2) |
| X175 | Isoperimetric point | − 1 + sec(A/2) cos(B/2) cos(C/2) |
| X179 | first Ajima-Malfatti point | sec4(A/4) |
| X181 | Apollonius point | a(b + c)2/(b + c − a) |
| X192 | Equal parallelians point | bc(ca + ab − bc) |
| X356 | Morley center | cos(A/3) + 2 cos(B/3) cos(C/3) |
| X360 | Hofstadter point | A/a |
| X401 | Bailey point | [sin(2B) sin(2C) − sin2(2A)] csc A |
Kimberling center
In honor of Clark Kimberling who created the online encyclopedia of more than 3500 triangle centers, the triangle centers listed in the encyclopedia are collectively called Kimberling centers.Polynomial triangle center
A triangle center P is called a polynomial triangle center if the trilinear coordinates of P can be expressed as polynomials in a, b and c.Regular triangle center
A triangle center P is called a regular triangle point if the trilinear coordinates of P can be expressed as polynomials in Δ, a, b and c, where Δ is the area of the triangle.Major triangle center
A triangle center P is said to be a major triangle center if the trilinear coordinates of P can be expressed in the form f(A) : f(B) : f(C) where f(A) is a function of A alone.Transcendental triangle center
A triangle center P is called a transcendental triangle center if P has no trilinear representation using only algebraic functions of a, b and c.Isosceles and equilateral triangles
Let f be a triangle center function. If two sides of a triangle are equal (say a = b) then- f(a, b, c) = f(b, a, c) since a = b
-
- = f(b, c, a) by bisymmetry
-
so two components of the associated triangle center are always equal. Therefore all triangle centers of an isosceles triangle must lie on its line of symmetry. For an equilateral triangle all three components are equal so all centers coincide with the centroid. So, like a circle, an equilateral triangle has a unique center.
Excenters
| Let f(a,b,c) = | 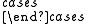 |
−1 | if a ≥ b and a ≥ c |
| 1 | otherwise |
This is readily seen to be a triangle center function and (provided the triangle is scalene) the corresponding triangle center is the excenter opposite to the largest vertex angle. The other two excenters can be picked out by similar functions. However as indicated above only one of the excenters of an isosceles triangle and none of the excenters of an equilateral triangle can ever be a triangle center.
Biantisymmetric functions
A function f is biantisymmetric if f(a,b,c) = −f(a,c,b) for all a,b,c. If such a function is also non-zero and homogeneous it is easily seen that the mapping (a,b,c) → f(a,b,c)2 f(b,c,a) f(c,a,b) is a triangle center function. The corresponding triangle center is f(a,b,c) : f(b,c,a) : f(c,a,b). On account of this the definition of triangle center function is sometimes taken to include non-zero homogeneous biantisymmetric functions.New centers from old
Any triangle center function f can be normalized by multiplying it by a symmetric function of a,b,c so that n = 0. A normalized triangle center function has the same triangle center as the original, and also the stronger property that f(ta,tb,tc) = f(a,b,c) for all t > 0 and all (a,b,c). Together with the zero function, normalized triangle center functions form an algebraAlgebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
under addition, subtraction, and multiplication. This gives an easy way to create new triangle centers. However distinct normalized triangle center functions will often define the same triangle center, for example f and (abc)−1(a+b+c)3f .
Uninteresting centers
Assume a,b,c are real variables and let α,β,γ be any three real constants. 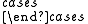 |
α | if a < b and a < c | (equivalently the first variable is the smallest) | |
| Let f(a,b,c) = | γ | if a > b and a > c | (equivalently the first variable is the largest) | |
| β | otherwise | (equivalently the first variable is in the middle) |
Then f is a triangle center function and α : β : γ is the corresponding triangle center whenever the sides of the reference triangle are labelled so that a < b < c. Thus every point is potentially a triangle center. However the vast majority of triangle centers are of little interest, just as most continuous functions are of little interest. The Encyclopedia of Triangle Centers
Encyclopedia of Triangle Centers
The Encyclopedia of Triangle Centers is an on-line list of more than 3,000 points or "centers" associated with the geometry of a triangle. It is maintained by Clark Kimberling, Professor of Mathematics at the University of Evansville....
is an ever-expanding list of interesting ones.
Barycentric coordinates
If f is a triangle center function then so is af and the corresponding triangle center is af(a,b,c) : bf(b,c,a) : cf(c,a,b). Since these are precisely the barycentric coordinates of the triangle center corresponding to f it follows that triangle centers could equally well have been defined in terms of barycentrics instead of trilinears. In practice it isn't difficult to switch from one coordinate system to the other.Binary systems
There are other center pairs besides the Fermat point and the 1st isogonic center. Another system is formed by X3 and the incenter of the tangential triangle. Consider the triangle center function given by :- 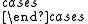 |
cos(A) | if the triangle is acute. | |
| f(a,b,c) = | cos(A) + sec(B)sec(C) | if the vertex angle at A is obtuse. | |
| cos(A) − sec(A) | if either of the angles at B or C is obtuse. |
For the corresponding triangle center there are four distinct possibilities :-
- cos(A) : cos(B) : cos(C) if the reference triangle is acute (this is also the circumcenter).
- cos(A) + sec(B)sec(C) : cos(B) − sec(B) : cos(C) − sec(C) if the angle at A is obtuse.
- cos(A) − sec(A) : cos(B) + sec(C)sec(A) : cos(C) − sec(C) if the angle at B is obtuse.
- cos(A) − sec(A) : cos(B) − sec(B) : cos(C) + sec(A)sec(B) if the angle at C is obtuse.
Routine calculation shows that in every case these trilinears represent the incenter of the tangential triangle. So this point is a triangle center that is a close companion of the circumcenter.
Bisymmetry and invariance
Reflecting a triangle reverses the order of its sides. In the image the coordinates refer to the (c,b,a) triangle and (using "|" as the separator) the reflection of an arbitrary point α : β : γ is γ | β | α. If f is a triangle center function the reflection of its triangle center is f(c,a,b) | f(b,c,a) | f(a,b,c) which, by bisymmetry, is the same as f(c,b,a) | f(b,a,c) | f(a,c,b). As this is also the triangle center corresponding to f relative to the (c,b,a) triangle, bisymmetry ensures that all triangle centers are invariant under reflection. Since rotations and translations may be regarded as double reflections they too must preserve triangle centers. These invariance properties provide justification for the definition.Alternative terminology
Some other names for dilation are uniform scalingScaling (geometry)
In Euclidean geometry, uniform scaling is a linear transformation that enlarges or shrinks objects by a scale factor that is the same in all directions. The result of uniform scaling is similar to the original...
, isotropic scaling
Scaling (geometry)
In Euclidean geometry, uniform scaling is a linear transformation that enlarges or shrinks objects by a scale factor that is the same in all directions. The result of uniform scaling is similar to the original...
, homothety, and homothecy.
Hyperbolic triangle centers
The study of triangle centers traditionally is concerned with Euclidean geometryEuclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, but triangle centers can also be studied in hyperbolic geometry
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
. Using gyrotrigonometry, trigonometric barycentric coordinates can be calculated that will coincide for euclidean and hyperbolic geometry. In order for the coordinates to coincide, the expressions must not encapsulate the specification of the anglesum being 180 degrees.
Tetrahedron centers and n-simplex centers
A generalization of triangle centers to higher dimensions is centers of tetrahedronTetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
s or higher-dimensional simplices
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
.
External links
- For detailed descriptions and nice diagrams of certain specific triangle centers: MathWorld–A Wolfram Web Resource:
- For a discussion on the distribution of triangle centers: The Triangle is a Busy Place – The Distribution of Triangle Centers Project (Accessed on 25 May 2009)
- URL of Clark Kimberling's Encyclopedia of Triangle centers: ETC
- Computer-Generated Encyclopedia of Euclidean Geometry The first part of the encyclopedia contains more than 3000 computer-generated statements of theorems in Triangle Geometry.
- A list of links to geometry pages in the internet: Links on Geometry

