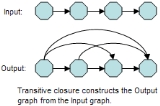
Transitive closure
Encyclopedia
In mathematics
, the transitive closure of a binary relation
R on a set X is the transitive relation
R+ on set X such that R+ contains R and R+ is minimal (Lidl and Pilz 1998:337). If the binary relation itself is transitive
, then the transitive closure will be that same binary relation; otherwise, the transitive closure will be a different relation. For example, if X is a set of airports and x R y means "there is a direct flight from airport x to airport y", then the transitive closure of R on X is the relation R+: "it is possible to fly from x to y in one or more flights."
One example of a non-transitive relation is "city x can be reached via a direct flight from city y" on the set of all cities. Simply because there is a direct flight from one city to a second city, and a direct flight from the second city to the third, does not imply there is a direct flight from the first city to the third. The transitive closure of this relation is a different relation, namely "there is a sequence of direct flights that begins at city x and ends at city y". Every relation can be extended in a similar way to a transitive relation.
of any family of transitive relations is again transitive. Furthermore, there exists at least one transitive relation containing R, namely the trivial one: X × X. The transitive closure of R is then given by the intersection of all transitive relations containing R.
We can describe the transitive closure of R in more concrete terms as follows, intuitively constructing it step by step. To start, define
and, for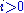
,
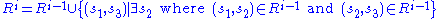
Each set in this construction takes the relation from the previous set, and adds any new elements necessary to make chains that are "one step" more transitive. The relation R+ is made by taking all of the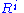
together, which we write as
To show that R+ is the transitive closure of R, we must show that it contains R, that it is transitive, and that it is the smallest set with both of those characteristics.
of two transitive relations need not be transitive. To preserve transitivity, one must take the transitive closure. This occurs, for example, when taking the union of two equivalence relation
s or two preorder
s. To obtain a new equivalence relation or preorder one must take the transitive closure (reflexivity and symmetry—in the case of equivalence relations—are automatic).
The transitive closure of a directed acyclic graph
or DAG is the reachability
relation of the DAG and a strict partial order.
the concept of transitive closure can be thought of as constructing a data structure that makes it possible to answer reachability questions. That is, can one get from node a to node d in one or more hops? A binary relation tells you only that node a is connected to node b, and that node b is connected to node c, etc. After the transitive closure is constructed, as depicted in the following figure, in an O(1) operation one may determine that node d is reachable from node a. The data structure is typically stored as a matrix, so if matrix[1][4] = 1, then it is the case that node 1 can reach node 4 through one or more hops.
, the complexity class
NL
corresponds precisely to the set of logical sentences expressible using first-order logic
together with transitive closure. This is because the transitive closure property has a close relationship with the NL-complete
problem STCON for finding directed paths in a graph. Similarly, the class L
is first-order logic with the commutative, transitive closure. When transitive closure is added to second-order logic
instead, we obtain PSPACE
.
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the transitive closure of a binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
R on a set X is the transitive relation
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
R+ on set X such that R+ contains R and R+ is minimal (Lidl and Pilz 1998:337). If the binary relation itself is transitive
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
, then the transitive closure will be that same binary relation; otherwise, the transitive closure will be a different relation. For example, if X is a set of airports and x R y means "there is a direct flight from airport x to airport y", then the transitive closure of R on X is the relation R+: "it is possible to fly from x to y in one or more flights."
Transitive relations and examples
A relation R on a set X is transitive if, for all x,y,z in X, whenever x R y and y R z then x R z. Examples of transitive relations include the equality relation on any set, the "less than or equal" relation on any linearly ordered set, and the relation "x was born before y" on the set of all people. Symbolically, this can be denoted as: if x < y and y < z then x < z.One example of a non-transitive relation is "city x can be reached via a direct flight from city y" on the set of all cities. Simply because there is a direct flight from one city to a second city, and a direct flight from the second city to the third, does not imply there is a direct flight from the first city to the third. The transitive closure of this relation is a different relation, namely "there is a sequence of direct flights that begins at city x and ends at city y". Every relation can be extended in a similar way to a transitive relation.
Existence and description
For any relation R, the transitive closure of R always exists. To see this, note that the intersectionIntersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of any family of transitive relations is again transitive. Furthermore, there exists at least one transitive relation containing R, namely the trivial one: X × X. The transitive closure of R is then given by the intersection of all transitive relations containing R.
We can describe the transitive closure of R in more concrete terms as follows, intuitively constructing it step by step. To start, define
and, for
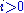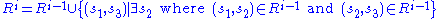
,Each set in this construction takes the relation from the previous set, and adds any new elements necessary to make chains that are "one step" more transitive. The relation R+ is made by taking all of the
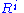together, which we write asTo show that R+ is the transitive closure of R, we must show that it contains R, that it is transitive, and that it is the smallest set with both of those characteristics.
-
: 
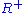contains all of the 
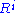, so in particular 
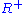contains 
. -
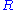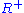is transitive: every element of 
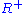is in one of the 
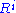, so 
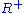must be transitive by the following reasoning: if 
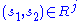and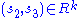 
, then from composition's associativity, 
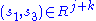(and thus in 
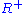) because of the definition of 
. -
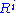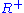is minimal: Let 
be any transitive relation containing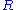 
, we want to show that 
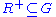. It is sufficient to show that for every 
, 
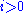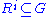. Well, since 
contains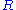 
, 
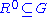. And since 
is transitive, whenever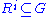 
, 
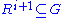according to the construction of 
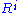and what it means to be transitive. Therefore, by induction, 
contains every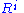 
, and thus also 
.
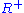Uses
Note that the unionUnion (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of two transitive relations need not be transitive. To preserve transitivity, one must take the transitive closure. This occurs, for example, when taking the union of two equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
s or two preorder
Preorder
In mathematics, especially in order theory, preorders are binary relations that are reflexive and transitive.For example, all partial orders and equivalence relations are preorders...
s. To obtain a new equivalence relation or preorder one must take the transitive closure (reflexivity and symmetry—in the case of equivalence relations—are automatic).
The transitive closure of a directed acyclic graph
Directed acyclic graph
In mathematics and computer science, a directed acyclic graph , is a directed graph with no directed cycles. That is, it is formed by a collection of vertices and directed edges, each edge connecting one vertex to another, such that there is no way to start at some vertex v and follow a sequence of...
or DAG is the reachability
Reachability
In graph theory, reachability is the notion of being able to get from one vertex in a directed graph to some other vertex. Note that reachability in undirected graphs is trivial — it is sufficient to find the connected components in the graph, which can be done in linear time.- Definition :For a...
relation of the DAG and a strict partial order.
Graph theory
In computer scienceComputer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
the concept of transitive closure can be thought of as constructing a data structure that makes it possible to answer reachability questions. That is, can one get from node a to node d in one or more hops? A binary relation tells you only that node a is connected to node b, and that node b is connected to node c, etc. After the transitive closure is constructed, as depicted in the following figure, in an O(1) operation one may determine that node d is reachable from node a. The data structure is typically stored as a matrix, so if matrix[1][4] = 1, then it is the case that node 1 can reach node 4 through one or more hops.
Relationship to complexity
In computational complexity theoryComputational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, the complexity class
Complexity class
In computational complexity theory, a complexity class is a set of problems of related resource-based complexity. A typical complexity class has a definition of the form:...
NL
NL (complexity)
In computational complexity theory, NL is the complexity class containing decision problems which can be solved by a nondeterministic Turing machine using a logarithmic amount of memory space....
corresponds precisely to the set of logical sentences expressible using first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
together with transitive closure. This is because the transitive closure property has a close relationship with the NL-complete
NL-complete
In computational complexity theory, NL-Complete is a complexity class which is complete for NL. It contains the most "difficult" or "expressive" problems in NL...
problem STCON for finding directed paths in a graph. Similarly, the class L
L (complexity)
In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space...
is first-order logic with the commutative, transitive closure. When transitive closure is added to second-order logic
Second-order logic
In logic and mathematics second-order logic is an extension of first-order logic, which itself is an extension of propositional logic. Second-order logic is in turn extended by higher-order logic and type theory....
instead, we obtain PSPACE
PSPACE
In computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :...
.
Algorithms
Efficient algorithms for computing the transitive closure of a graph can be found here. The simplest technique is probably the Floyd–Warshall algorithm. The fastest worst-case methods, which are not practical, reduce the problem to matrix multiplicationMatrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
.
See also
- Transitive reductionTransitive reductionIn mathematics, a transitive reduction of a binary relation R on a set X is a minimal relation R' on X such that the transitive closure of R' is the same as the transitive closure of R. If the transitive closure of R is antisymmetric and finite, then R' is unique...
(a smallest relation having the transitive closure of R as its transitive closure) - Symmetric closureSymmetric closureIn mathematics, the symmetric closure of a binary relation R on a set X is the smallest symmetric relation on X that contains R....
- Reflexive closureReflexive closureIn mathematics, the reflexive closure of a binary relation R on a set X is the smallest reflexive relation on X that contains R....
- Ancestral relationAncestral relationIn mathematical logic, the ancestral relation of an arbitrary binary relation R is defined below.The ancestral makes its first appearance in Frege's Begriffsschrift. Frege later employed it in his Grundgesetze as part of his definition of the natural numbers...
External links
- "Transitive closure and reduction", The Stony Brook Algorithm Repository, Steven Skiena .