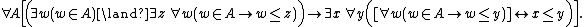Second-order logic
Encyclopedia
In logic
and mathematics
second-order logic is an extension of first-order logic
, which itself is an extension of propositional logic. Second-order logic is in turn extended by higher-order logic
and type theory
.
First-order logic uses only variables that range over individuals (elements of the domain of discourse
); second-order logic has these variables as well as additional variables that range over sets of individuals. For example, the second-order sentence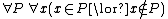 says that for every set P of individuals and every individual x, either x is in P or it is not (this is the principle of bivalence
says that for every set P of individuals and every individual x, either x is in P or it is not (this is the principle of bivalence
). Second-order logic also includes variables quantifying over functions, and other variables as explained in the section Syntax below. Both first-order and second-order logic use the idea of a domain of discourse
(often called simply the "domain" or the "universe"). The domain is a set of individual elements which can be quantified
over.
s, one can assert in first-order logic the existence of an additive inverse of each real number by writing ∀x ∃y (x + y = 0) but one needs second-order logic to assert the least-upper-bound
property for sets of real numbers, which states that every bounded, nonempty set of real numbers has a supremum
. If the domain is the set of all real numbers, the following second-order sentence expresses the least upper bound property:
In second-order logic, it is possible to write formal sentences which say "the domain is finite" or "the domain is of countable
cardinality." To say that the domain is finite, use the sentence that says that every surjective function from the domain to itself is injective. To say that the domain has countable cardinality, use the sentence that says that there is a bijection
between every two infinite subsets of the domain. It follows from the compactness theorem
and the upward Löwenheim–Skolem theorem that it is not possible to characterize finiteness or countability, respectively, in first-order logic.
For each of the sorts of variable just defined, it is permissible to build up formulas by using universal and/or existential quantifiers. Thus there are many sorts of quantifiers, two for each sort of variable.
A sentence in second-order logic, as in first-order logic, is a well-formed formula with no free variables (of any sort).
In monadic second-order logic (MSOL), only variables for subsets of the domain are added. The second-order logic with all the sorts of variables just described is sometimes called full second-order logic to distinguish it from the monadic version.
Just as in first-order logic, second-order logic may include non-logical symbols in a particular second-order language. These are restricted, however, in that all terms that they form must be either first-order terms (which can be substituted for a first-order variable) or second-order terms (which can be substituted for a second-order variable of an appropriate sort).
In standard semantics, also called full semantics, the quantifiers range over all sets or functions of the appropriate sort. Thus once the domain of the first-order variables is established, the meaning of the remaining quantifiers is fixed. It is these semantics that give second-order logic its expressive power, and they will be assumed for the remainder of this article.
In Henkin semantics, each sort of second-order variable has a particular domain of its own to range over, which may be a proper subset of all sets or functions of that sort. Leon Henkin
(1950) defined these semantics and proved that Gödel's completeness theorem
and compactness theorem
, which hold for first-order logic, carry over to second-order logic with Henkin semantics. This is because Henkin semantics are almost identical to many-sorted first-order semantics, where additional sorts of variables are added to simulate the new variables of second-order logic. Second-order logic with Henkin semantics is not more expressive than first-order logic. Henkin semantics are commonly used in the study of second-order arithmetic
.
for a logic is a set of inference rules and logical axioms that determine which sequences of formulas constitute valid proofs. Several deductive systems can be used for second-order logic, although none can be complete for the standard semantics (see below). Each of these systems is sound
, which means any sentence they can be used to prove is logically valid in the appropriate semantics.
The weakest deductive system that can be used consists of a standard deductive system for first-order logic (such as natural deduction
) augmented with substitution rules for second-order terms. This deductive system is commonly used in the study of second-order arithmetic
.
The deductive systems considered by Shapiro (1991) and Henkin (1950) add to the augmented first-order deductive scheme both comprehension axioms and choice axioms. These axioms are sound for standard second-order semantics. They are sound for Henkin semantics if only Henkin models that satisfy the comprehension and choice axioms are considered.
But notice that the domain was asserted to include all sets of real numbers. That requirement cannot be reduced to a first-order sentence, as the Löwenheim-Skolem theorem shows. That theorem implies that there is some countably infinite subset of the real numbers, whose members we will call internal numbers, and some countably infinite collection of sets of internal numbers, whose members we will call "internal sets", such that the domain consisting of internal numbers and internal sets satisfies exactly the same first-order sentences satisfied as the domain of real-numbers-and-sets-of-real-numbers. In particular, it satisfies a sort of least-upper-bound axiom that says, in effect:
Countability of the set of all internal numbers (in conjunction with the fact that those form a densely ordered set) implies that that set does not satisfy the full least-upper-bound axiom. Countability of the set of all internal sets implies that it is not the set of all subsets of the set of all internal numbers (since Cantor's theorem
implies that the set of all subsets of a countably infinite set is an uncountably infinite set). This construction is closely related to Skolem's paradox
.
Thus the first-order theory of real numbers and sets of real numbers has many models, some of which are countable. The second-order theory of the real numbers has only one model, however.
This follows from the classical theorem that there is only one Archimedean
complete ordered field
, along with the fact that all the axioms of an Archimedean complete ordered field are expressible in second-order logic. This shows that the second-order theory of the real numbers cannot be reduced to a first-order theory, in the sense that the second-order theory of the real numbers has only one model but the corresponding first-order theory has many models.
There are more extreme examples showing that second-order logic with standard semantics is more expressive than first-order logic. There is a finite second-order theory whose only model is the real numbers if the continuum hypothesis
holds and which has no model if the continuum hypothesis does not hold (cf. Shapiro 2000 p. 105). This theory consists of a finite theory characterizing the real numbers as a complete Archimedean ordered field plus an axiom saying that the domain is of the first uncountable cardinality. This example illustrates that the question of whether a sentence in second-order logic is consistent is extremely subtle.
Additional limitations of second order logic are described in the next section.
This corollary is sometimes expressed by saying that second-order logic does not admit a complete proof theory
. In this respect second-order logic with standard semantics differs from first-order logic; Quine (1970, pp. 90–91) pointed to the lack of a complete proof system as a reason for thinking of second-order logic as not logic, properly speaking.
As mentioned above, Henkin proved that the standard deductive system for first-order logic is sound, complete, and effective for second-order logic with Henkin semantics, and the deductive system with comprehension and choice principles is sound, complete, and effective for Henkin semantics using only models that satisfy these principles.
and Alfred North Whitehead
made them famous. Frege used different variables to distinguish quantification over objects from quantification over properties and sets; but he did not see himself as doing two different kinds of logic. After the discovery of Russell's paradox
it was realized that something was wrong with his system. Eventually logicians found that restricting Frege's logic in various ways—to what is now called first-order logic—eliminated this problem: sets and properties cannot be quantified over in first-order-logic alone. The now-standard hierarchy of orders of logics dates from this time.
It was found that set theory
could be formulated as an axiomatized system within the apparatus of first-order logic (at the cost of several kinds of completeness
, but nothing so bad as Russell's paradox), and this was done (see Zermelo-Fraenkel set theory), as sets are vital for mathematics
. Arithmetic
, mereology
, and a variety of other powerful logical theories could be formulated axiomatically without appeal to any more logical apparatus than first-order quantification, and this, along with Gödel and Skolem's adherence to first-order logic, led to a general decline in work in second (or any higher) order logic.
This rejection was actively advanced by some logicians, most notably W. V. Quine. Quine advanced the view that in predicate-language sentences like Fx the "x" is to be thought of as a variable or name denoting an object and hence can be quantified over, as in "For all things, it is the case that . . ." but the "F" is to be thought of as an abbreviation for an incomplete sentence, not the name of an object (not even of an abstract object
like a property). For example, it might mean " . . . is a dog." But it makes no sense to think we can quantify over something like this. (Such a position is quite consistent with Frege's own arguments on the concept-object distinction). So to use a predicate as a variable is to have it occupy the place of a name which only individual variables should occupy. This reasoning has been rejected by Boolos.
In recent years second-order logic has made something of a recovery, buoyed by George Boolos
' interpretation of second-order quantification as plural quantification
over the same domain of objects as first-order quantification (Boolos 1984). Boolos furthermore points to the claimed nonfirstorderizability
of sentences such as "Some critics admire only each other" and "Some of Fianchetto's men went into the warehouse unaccompanied by anyone else" which he argues can only be expressed by the full force of second-order quantification. However, generalized quantification and partially-ordered, or branching, quantification may suffice to express a certain class of purportedly nonfirstorderizable sentences as well and it does not appeal to second-order quantification.
The expressive power of various forms of second-order logic on finite structures is intimately tied to computational complexity theory
. The field of descriptive complexity
studies which computational complexity class
es can be characterized by the power of the logic needed to express languages (sets of finite strings) in them. A string w = w1···wn in a finite alphabet A can be represented by a finite structure with domain D = {1,...,n}, unary predicates Pa for each a ∈ A, satisfied by those indices i such that wi = a, and additional predicates which serve to uniquely identify which index is which (typically, one takes the graph of the successor function on D or the order relation <, possibly with other arithmetic predicates). Conversely, the table of any finite structure can be encoded by a finite string.
With this identification, we have the following characterizations of variants of second-order logic over finite structures:
Relationships among these classes directly impact the relative expressiveness of the logics over finite structures; for example, if PH = PSPACE, then adding a transitive closure operator to second-order logic would not make it any more expressive over finite structures.
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
and mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
second-order logic is an extension of first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
, which itself is an extension of propositional logic. Second-order logic is in turn extended by higher-order logic
Higher-order logic
In mathematics and logic, a higher-order logic is a form of predicate logic that is distinguished from first-order logic by additional quantifiers and a stronger semantics...
and type theory
Type theory
In mathematics, logic and computer science, type theory is any of several formal systems that can serve as alternatives to naive set theory, or the study of such formalisms in general...
.
First-order logic uses only variables that range over individuals (elements of the domain of discourse
Domain of discourse
In the formal sciences, the domain of discourse, also called the universe of discourse , is the set of entities over which certain variables of interest in some formal treatment may range...
); second-order logic has these variables as well as additional variables that range over sets of individuals. For example, the second-order sentence
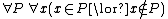 says that for every set P of individuals and every individual x, either x is in P or it is not (this is the principle of bivalence
says that for every set P of individuals and every individual x, either x is in P or it is not (this is the principle of bivalencePrinciple of bivalence
In logic, the semantic principle of bivalence states that every declarative sentence expressing a proposition has exactly one truth value, either true or false...
). Second-order logic also includes variables quantifying over functions, and other variables as explained in the section Syntax below. Both first-order and second-order logic use the idea of a domain of discourse
Domain of discourse
In the formal sciences, the domain of discourse, also called the universe of discourse , is the set of entities over which certain variables of interest in some formal treatment may range...
(often called simply the "domain" or the "universe"). The domain is a set of individual elements which can be quantified
Quantification
Quantification has several distinct senses. In mathematics and empirical science, it is the act of counting and measuring that maps human sense observations and experiences into members of some set of numbers. Quantification in this sense is fundamental to the scientific method.In logic,...
over.
Expressive power
Second-order logic is more expressive than first-order logic. For example, if the domain is the set of all real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, one can assert in first-order logic the existence of an additive inverse of each real number by writing ∀x ∃y (x + y = 0) but one needs second-order logic to assert the least-upper-bound
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
property for sets of real numbers, which states that every bounded, nonempty set of real numbers has a supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
. If the domain is the set of all real numbers, the following second-order sentence expresses the least upper bound property:
In second-order logic, it is possible to write formal sentences which say "the domain is finite" or "the domain is of countable
Countable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
cardinality." To say that the domain is finite, use the sentence that says that every surjective function from the domain to itself is injective. To say that the domain has countable cardinality, use the sentence that says that there is a bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
between every two infinite subsets of the domain. It follows from the compactness theorem
Compactness theorem
In mathematical logic, the compactness theorem states that a set of first-order sentences has a model if and only if every finite subset of it has a model...
and the upward Löwenheim–Skolem theorem that it is not possible to characterize finiteness or countability, respectively, in first-order logic.
Syntax
The syntax of second-order logic tells which expressions are well formed formulas. In addition to the syntax of first-order logic, second-order logic includes many new sorts (sometimes called types) of variables. These are:- A sort of variables that range over sets of individuals. If S is a variable of this sort and t is a first-order term then the expression t ∈ S (also written S(t) or St) is an atomic formulaAtomic formulaIn mathematical logic, an atomic formula is a formula with no deeper propositional structure, that is, a formula that contains no logical connectives or equivalently a formula that has no strict subformulas. Atoms are thus the simplest well-formed formulas of the logic...
. Sets of individuals can also be viewed as unary relations on the domain. - For each natural number k there is a sort of variable that ranges over all k-ary relations on the individuals. If R is such a k-ary relation variable and t1,..., tk are first-order terms then the expression R(t1,...,tk) is an atomic formula.
- For each natural number k there is a sort of variable that ranges over functions that take k elements of the domain and return a single element of the domain. If f is such a k-ary function symbol and t1,...,tk are first-order terms then the expression f(t1,...,tk) is a first-order term.
For each of the sorts of variable just defined, it is permissible to build up formulas by using universal and/or existential quantifiers. Thus there are many sorts of quantifiers, two for each sort of variable.
A sentence in second-order logic, as in first-order logic, is a well-formed formula with no free variables (of any sort).
In monadic second-order logic (MSOL), only variables for subsets of the domain are added. The second-order logic with all the sorts of variables just described is sometimes called full second-order logic to distinguish it from the monadic version.
Just as in first-order logic, second-order logic may include non-logical symbols in a particular second-order language. These are restricted, however, in that all terms that they form must be either first-order terms (which can be substituted for a first-order variable) or second-order terms (which can be substituted for a second-order variable of an appropriate sort).
Semantics
The semantics of second-order logic establish the meaning of each sentence. Unlike first-order logic, which has only one standard semantics, there are two different semantics that are commonly used for second-order logic: standard semantics and Henkin semantics. In each of these semantics, the interpretations of the first-order quantifiers and the logical connectives are the same as in first-order logic. Only the ranges of quantifiers over second-order variables differ in the two types of semantics.In standard semantics, also called full semantics, the quantifiers range over all sets or functions of the appropriate sort. Thus once the domain of the first-order variables is established, the meaning of the remaining quantifiers is fixed. It is these semantics that give second-order logic its expressive power, and they will be assumed for the remainder of this article.
In Henkin semantics, each sort of second-order variable has a particular domain of its own to range over, which may be a proper subset of all sets or functions of that sort. Leon Henkin
Leon Henkin
Leon Albert Henkin was a logician at the University of California, Berkeley. He was principally known for the "Henkin's completeness proof": his version of the proof of the semantic completeness of standard systems of first-order logic.-The completeness proof:Henkin's result was not novel; it had...
(1950) defined these semantics and proved that Gödel's completeness theorem
Gödel's completeness theorem
Gödel's completeness theorem is a fundamental theorem in mathematical logic that establishes a correspondence between semantic truth and syntactic provability in first-order logic. It was first proved by Kurt Gödel in 1929....
and compactness theorem
Compactness theorem
In mathematical logic, the compactness theorem states that a set of first-order sentences has a model if and only if every finite subset of it has a model...
, which hold for first-order logic, carry over to second-order logic with Henkin semantics. This is because Henkin semantics are almost identical to many-sorted first-order semantics, where additional sorts of variables are added to simulate the new variables of second-order logic. Second-order logic with Henkin semantics is not more expressive than first-order logic. Henkin semantics are commonly used in the study of second-order arithmetic
Second-order arithmetic
In mathematical logic, second-order arithmetic is a collection of axiomatic systems that formalize the natural numbers and their subsets. It is an alternative to axiomatic set theory as a foundation for much, but not all, of mathematics. It was introduced by David Hilbert and Paul Bernays in their...
.
Deductive systems
A deductive systemDeductive system
A deductive system consists of the axioms and rules of inference that can be used to derive the theorems of the system....
for a logic is a set of inference rules and logical axioms that determine which sequences of formulas constitute valid proofs. Several deductive systems can be used for second-order logic, although none can be complete for the standard semantics (see below). Each of these systems is sound
Soundness
In mathematical logic, a logical system has the soundness property if and only if its inference rules prove only formulas that are valid with respect to its semantics. In most cases, this comes down to its rules having the property of preserving truth, but this is not the case in general. The word...
, which means any sentence they can be used to prove is logically valid in the appropriate semantics.
The weakest deductive system that can be used consists of a standard deductive system for first-order logic (such as natural deduction
Natural deduction
In logic and proof theory, natural deduction is a kind of proof calculus in which logical reasoning is expressed by inference rules closely related to the "natural" way of reasoning...
) augmented with substitution rules for second-order terms. This deductive system is commonly used in the study of second-order arithmetic
Second-order arithmetic
In mathematical logic, second-order arithmetic is a collection of axiomatic systems that formalize the natural numbers and their subsets. It is an alternative to axiomatic set theory as a foundation for much, but not all, of mathematics. It was introduced by David Hilbert and Paul Bernays in their...
.
The deductive systems considered by Shapiro (1991) and Henkin (1950) add to the augmented first-order deductive scheme both comprehension axioms and choice axioms. These axioms are sound for standard second-order semantics. They are sound for Henkin semantics if only Henkin models that satisfy the comprehension and choice axioms are considered.
Non-reducibility to first-order logic
One might attempt to reduce the second-order theory of the real numbers, with full second-order semantics, to the first-order theory in the following way. First expand the domain from the set of all real numbers to a two-sorted domain, with the second sort containing all sets of real numbers. Add a new binary predicate to the language: the membership relation. Then sentences that were second-order become first-order, with the formerly second-order quantifiers ranging over the second sort instead. This reduction can be attempted in a one-sorted theory by adding unary predicates that tell whether an element is a number or a set, and taking the domain to be the union of the set of real numbers and the power set of the real numbers.But notice that the domain was asserted to include all sets of real numbers. That requirement cannot be reduced to a first-order sentence, as the Löwenheim-Skolem theorem shows. That theorem implies that there is some countably infinite subset of the real numbers, whose members we will call internal numbers, and some countably infinite collection of sets of internal numbers, whose members we will call "internal sets", such that the domain consisting of internal numbers and internal sets satisfies exactly the same first-order sentences satisfied as the domain of real-numbers-and-sets-of-real-numbers. In particular, it satisfies a sort of least-upper-bound axiom that says, in effect:
- Every nonempty internal set that has an internal upper bound has a least internal upper bound.
Countability of the set of all internal numbers (in conjunction with the fact that those form a densely ordered set) implies that that set does not satisfy the full least-upper-bound axiom. Countability of the set of all internal sets implies that it is not the set of all subsets of the set of all internal numbers (since Cantor's theorem
Cantor's theorem
In elementary set theory, Cantor's theorem states that, for any set A, the set of all subsets of A has a strictly greater cardinality than A itself...
implies that the set of all subsets of a countably infinite set is an uncountably infinite set). This construction is closely related to Skolem's paradox
Skolem's paradox
In mathematical logic and philosophy, Skolem's paradox is a seeming contradiction that arises from the downward Löwenheim–Skolem theorem. Thoralf Skolem was the first to discuss the seemingly contradictory aspects of the theorem, and to discover the relativity of set-theoretic notions now known as...
.
Thus the first-order theory of real numbers and sets of real numbers has many models, some of which are countable. The second-order theory of the real numbers has only one model, however.
This follows from the classical theorem that there is only one Archimedean
Archimedean property
In abstract algebra and analysis, the Archimedean property, named after the ancient Greek mathematician Archimedes of Syracuse, is a property held by some ordered or normed groups, fields, and other algebraic structures. Roughly speaking, it is the property of having no infinitely large or...
complete ordered field
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
, along with the fact that all the axioms of an Archimedean complete ordered field are expressible in second-order logic. This shows that the second-order theory of the real numbers cannot be reduced to a first-order theory, in the sense that the second-order theory of the real numbers has only one model but the corresponding first-order theory has many models.
There are more extreme examples showing that second-order logic with standard semantics is more expressive than first-order logic. There is a finite second-order theory whose only model is the real numbers if the continuum hypothesis
Continuum hypothesis
In mathematics, the continuum hypothesis is a hypothesis, advanced by Georg Cantor in 1874, about the possible sizes of infinite sets. It states:Establishing the truth or falsehood of the continuum hypothesis is the first of Hilbert's 23 problems presented in the year 1900...
holds and which has no model if the continuum hypothesis does not hold (cf. Shapiro 2000 p. 105). This theory consists of a finite theory characterizing the real numbers as a complete Archimedean ordered field plus an axiom saying that the domain is of the first uncountable cardinality. This example illustrates that the question of whether a sentence in second-order logic is consistent is extremely subtle.
Additional limitations of second order logic are described in the next section.
Metalogical results
It is a corollary of Gödel's incompleteness theorem that there is no deductive system (that is, no notion of provability) for second-order formulas that simultaneously satisfies these three desired attributes:- (SoundnessSoundnessIn mathematical logic, a logical system has the soundness property if and only if its inference rules prove only formulas that are valid with respect to its semantics. In most cases, this comes down to its rules having the property of preserving truth, but this is not the case in general. The word...
) Every provable second-order sentence is universally valid, i.e., true in all domains under standard semantics.
- (CompletenessCompletenessIn general, an object is complete if nothing needs to be added to it. This notion is made more specific in various fields.-Logical completeness:In logic, semantic completeness is the converse of soundness for formal systems...
) Every universally valid second-order formula, under standard semantics, is provable.
- (EffectivenessDecidability (logic)In logic, the term decidable refers to the decision problem, the question of the existence of an effective method for determining membership in a set of formulas. Logical systems such as propositional logic are decidable if membership in their set of logically valid formulas can be effectively...
) There is a proof-checking algorithm that can correctly decide whether a given sequence of symbols is a valid proof or not.
This corollary is sometimes expressed by saying that second-order logic does not admit a complete proof theory
Proof theory
Proof theory is a branch of mathematical logic that represents proofs as formal mathematical objects, facilitating their analysis by mathematical techniques. Proofs are typically presented as inductively-defined data structures such as plain lists, boxed lists, or trees, which are constructed...
. In this respect second-order logic with standard semantics differs from first-order logic; Quine (1970, pp. 90–91) pointed to the lack of a complete proof system as a reason for thinking of second-order logic as not logic, properly speaking.
As mentioned above, Henkin proved that the standard deductive system for first-order logic is sound, complete, and effective for second-order logic with Henkin semantics, and the deductive system with comprehension and choice principles is sound, complete, and effective for Henkin semantics using only models that satisfy these principles.
History and disputed value
Predicate logic was primarily introduced to the mathematical community by C. S. Peirce, who coined the term second-order logic and whose notation is most similar to the modern form (Putnam 1982). However, today most students of logic are more familiar with the works of Frege, who actually published his work several years prior to Peirce but whose works remained in obscurity until Bertrand RussellBertrand Russell
Bertrand Arthur William Russell, 3rd Earl Russell, OM, FRS was a British philosopher, logician, mathematician, historian, and social critic. At various points in his life he considered himself a liberal, a socialist, and a pacifist, but he also admitted that he had never been any of these things...
and Alfred North Whitehead
Alfred North Whitehead
Alfred North Whitehead, OM FRS was an English mathematician who became a philosopher. He wrote on algebra, logic, foundations of mathematics, philosophy of science, physics, metaphysics, and education...
made them famous. Frege used different variables to distinguish quantification over objects from quantification over properties and sets; but he did not see himself as doing two different kinds of logic. After the discovery of Russell's paradox
Russell's paradox
In the foundations of mathematics, Russell's paradox , discovered by Bertrand Russell in 1901, showed that the naive set theory created by Georg Cantor leads to a contradiction...
it was realized that something was wrong with his system. Eventually logicians found that restricting Frege's logic in various ways—to what is now called first-order logic—eliminated this problem: sets and properties cannot be quantified over in first-order-logic alone. The now-standard hierarchy of orders of logics dates from this time.
It was found that set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
could be formulated as an axiomatized system within the apparatus of first-order logic (at the cost of several kinds of completeness
Completeness
In general, an object is complete if nothing needs to be added to it. This notion is made more specific in various fields.-Logical completeness:In logic, semantic completeness is the converse of soundness for formal systems...
, but nothing so bad as Russell's paradox), and this was done (see Zermelo-Fraenkel set theory), as sets are vital for mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
. Arithmetic
Arithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
, mereology
Mereology
In philosophy and mathematical logic, mereology treats parts and the wholes they form...
, and a variety of other powerful logical theories could be formulated axiomatically without appeal to any more logical apparatus than first-order quantification, and this, along with Gödel and Skolem's adherence to first-order logic, led to a general decline in work in second (or any higher) order logic.
This rejection was actively advanced by some logicians, most notably W. V. Quine. Quine advanced the view that in predicate-language sentences like Fx the "x" is to be thought of as a variable or name denoting an object and hence can be quantified over, as in "For all things, it is the case that . . ." but the "F" is to be thought of as an abbreviation for an incomplete sentence, not the name of an object (not even of an abstract object
Abstract object
An abstract object is an object which does not exist at any particular time or place, but rather exists as a type of thing . In philosophy, an important distinction is whether an object is considered abstract or concrete. Abstract objects are sometimes called abstracta An abstract object is an...
like a property). For example, it might mean " . . . is a dog." But it makes no sense to think we can quantify over something like this. (Such a position is quite consistent with Frege's own arguments on the concept-object distinction). So to use a predicate as a variable is to have it occupy the place of a name which only individual variables should occupy. This reasoning has been rejected by Boolos.
In recent years second-order logic has made something of a recovery, buoyed by George Boolos
George Boolos
George Stephen Boolos was a philosopher and a mathematical logician who taught at the Massachusetts Institute of Technology.- Life :...
' interpretation of second-order quantification as plural quantification
Plural quantification
In mathematics and logic, plural quantification is the theory that an individual variable x may take on plural, as well as singular values. As well as substituting individual objects such as Alice, the number 1, the tallest building in London etc...
over the same domain of objects as first-order quantification (Boolos 1984). Boolos furthermore points to the claimed nonfirstorderizability
Nonfirstorderizability
In formal logic, nonfirstorderizability is the inability of an expression to be adequately captured in particular theories in first-order logic. Nonfirstorderizable sentences are sometimes presented as evidence that first-order logic is not adequate to capture the nuances of meaning in natural...
of sentences such as "Some critics admire only each other" and "Some of Fianchetto's men went into the warehouse unaccompanied by anyone else" which he argues can only be expressed by the full force of second-order quantification. However, generalized quantification and partially-ordered, or branching, quantification may suffice to express a certain class of purportedly nonfirstorderizable sentences as well and it does not appeal to second-order quantification.
Applications to complexity
The expressive power of various forms of second-order logic on finite structures is intimately tied to computational complexity theory
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
. The field of descriptive complexity
Descriptive complexity
Descriptive complexity is a branch of computational complexity theory and of finite model theory that characterizes complexity classes by the type of logic needed to express the languages in them. For example, PH, the union of all complexity classes in the polynomial hierarchy, is precisely the...
studies which computational complexity class
Complexity class
In computational complexity theory, a complexity class is a set of problems of related resource-based complexity. A typical complexity class has a definition of the form:...
es can be characterized by the power of the logic needed to express languages (sets of finite strings) in them. A string w = w1···wn in a finite alphabet A can be represented by a finite structure with domain D = {1,...,n}, unary predicates Pa for each a ∈ A, satisfied by those indices i such that wi = a, and additional predicates which serve to uniquely identify which index is which (typically, one takes the graph of the successor function on D or the order relation <, possibly with other arithmetic predicates). Conversely, the table of any finite structure can be encoded by a finite string.
With this identification, we have the following characterizations of variants of second-order logic over finite structures:
- NPNP (complexity)In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
is the set of languages definable by existential, second-order formulas (Fagin's theoremFagin's theoremFagin's theorem is a result in descriptive complexity theory that states that the set of all properties expressible in existential second-order logic is precisely the complexity class NP...
, 1974). - co-NP is the set of languages definable by universal, second-order formulas.
- PH is the set of languages definable by second-order formulas.
- PSPACEPSPACEIn computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :...
is the set of languages definable by second-order formulas with an added transitive closureTransitive closureIn mathematics, the transitive closure of a binary relation R on a set X is the transitive relation R+ on set X such that R+ contains R and R+ is minimal . If the binary relation itself is transitive, then the transitive closure will be that same binary relation; otherwise, the transitive closure...
operator. - EXPTIMEEXPTIMEIn computational complexity theory, the complexity class EXPTIME is the set of all decision problems solvable by a deterministic Turing machine in O time, where p is a polynomial function of n....
is the set of languages definable by second-order formulas with an added least fixed pointLeast fixed pointIn order theory, a branch of mathematics, the least fixed point of a function is the fixed point which is less than or equal to all other fixed points, according to some partial order....
operator.
Relationships among these classes directly impact the relative expressiveness of the logics over finite structures; for example, if PH = PSPACE, then adding a transitive closure operator to second-order logic would not make it any more expressive over finite structures.