
Toroidal coordinates
Encyclopedia

Orthogonal coordinates
In mathematics, orthogonal coordinates are defined as a set of d coordinates q = in which the coordinate surfaces all meet at right angles . A coordinate surface for a particular coordinate qk is the curve, surface, or hypersurface on which qk is a constant...
coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
that results from rotating the two-dimensional bipolar coordinate system
Bipolar coordinates
Bipolar coordinates are a two-dimensional orthogonal coordinate system. There are two commonly defined types of bipolar coordinates. The other system is two-center bipolar coordinates. There is also a third coordinate system that is based on two poles . The first is based on the Apollonian circles...
about the axis that separates its two foci. Thus, the two foci
Focus (geometry)
In geometry, the foci are a pair of special points with reference to which any of a variety of curves is constructed. For example, foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola...
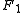 and
and 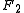 in bipolar coordinates
in bipolar coordinatesBipolar coordinates
Bipolar coordinates are a two-dimensional orthogonal coordinate system. There are two commonly defined types of bipolar coordinates. The other system is two-center bipolar coordinates. There is also a third coordinate system that is based on two poles . The first is based on the Apollonian circles...
become a ring of radius
 in the
in the 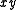 plane of the toroidal coordinate system; the
plane of the toroidal coordinate system; the  -axis is the axis of rotation. The focal ring is also known as the reference circle.
-axis is the axis of rotation. The focal ring is also known as the reference circle.Definition
The most common definition of toroidal coordinates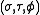 is
is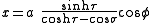
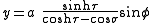
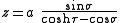
where the
 coordinate of a point
coordinate of a point  equals the angle
equals the angle  and the
and the  coordinate equals the natural logarithm
coordinate equals the natural logarithmNatural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
of the ratio of the distances
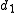 and
and 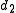 to opposite sides of the focal ring
to opposite sides of the focal ring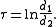
The coordinate ranges are
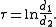 and
and 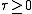 and
and 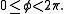
Coordinate surfaces
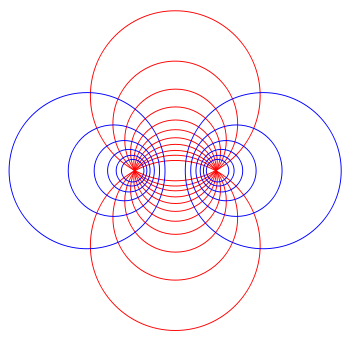
 correspond to spheres of different radii
correspond to spheres of different radii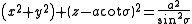
that all pass through the focal ring but are not concentric. The surfaces of constant
 are non-intersecting tori of different radii
are non-intersecting tori of different radii
that surround the focal ring. The centers of the constant-
 spheres lie along the
spheres lie along the  -axis, whereas the constant-
-axis, whereas the constant- tori are centered in the
tori are centered in the 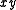 plane.
plane.Inverse transformation
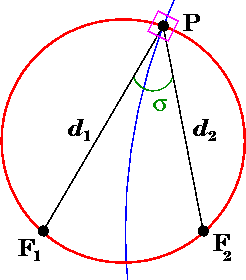
The (σ, τ, φ) coordinates may be calculated from the Cartesian coordinates (x, y, z) as follows. The azimuthal angle φ is given by the formula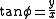
The cylindrical radius ρ of the point P is given by
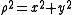
and its distances to the foci in the plane defined by φ is given by
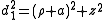
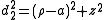
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
of the focal distances

whereas the coordinate σ equals the angle between the rays to the foci, which may be determined from the law of cosines
Law of cosines
In trigonometry, the law of cosines relates the lengths of the sides of a plane triangle to the cosine of one of its angles. Using notation as in Fig...
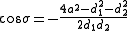
where the sign of σ is determined by whether the coordinate surface sphere is above or below the x-y plane.
Scale factors
The scale factors for the toroidal coordinates and
and  are equal
are equal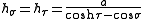
whereas the azimuthal scale factor equals
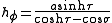
Thus, the infinitesimal volume element equals

and the Laplacian is given by
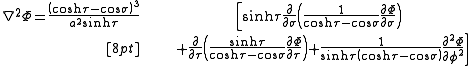
Other differential operators such as
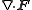
and
 can be expressed in the coordinates
can be expressed in the coordinates  by substituting
by substitutingthe scale factors into the general formulae
found in orthogonal coordinates
Orthogonal coordinates
In mathematics, orthogonal coordinates are defined as a set of d coordinates q = in which the coordinate surfaces all meet at right angles . A coordinate surface for a particular coordinate qk is the curve, surface, or hypersurface on which qk is a constant...
.
Standard separation
The 3-variable Laplace equation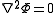
admits solution via separation of variables
Separation of variables
In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....
in toroidal coordinates. Making the substitution
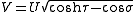
A separable equation is then obtained. A particular solution obtained by separation of variables
Separation of variables
In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....
is:

where each function is a linear combination of:
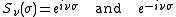
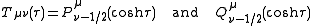
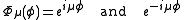
Where P and Q are associated Legendre functions of the first and second kind. These Legendre functions are often referred to as toroidal harmonics.
Toroidal harmonics have many interesting properties. If you make a variable substitution
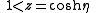 then, for instance, with vanishing order (the convention is to not write the order when it vanishes) and
then, for instance, with vanishing order (the convention is to not write the order when it vanishes) and 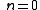

and
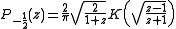
where
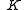 and
and 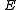 are the complete elliptic integrals of the first and second kind respectively. The rest of the toroidal harmonics can be obtained, for instance, in terms of the complete elliptic integrals, by using recurrence relations for associated Legendre functions.
are the complete elliptic integrals of the first and second kind respectively. The rest of the toroidal harmonics can be obtained, for instance, in terms of the complete elliptic integrals, by using recurrence relations for associated Legendre functions.The classic applications of toroidal coordinates are in solving partial differential equations,
e.g., Laplace's equation
Laplace's equation
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
for which toroidal coordinates allow a separation of variables
Separation of variables
In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....
or the Helmholtz equation
Helmholtz equation
The Helmholtz equation, named for Hermann von Helmholtz, is the elliptic partial differential equation\nabla^2 A + k^2 A = 0where ∇2 is the Laplacian, k is the wavenumber, and A is the amplitude.-Motivation and uses:...
, for which toroidal coordinates do not allow a separation of variables. Typical examples would be the electric potential
Electric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
and electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
of a conducting torus, or in the degenerate case, a conducting ring.
An alternative separation
Alternatively, a different substitution may be made (Andrews 2006)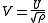
where
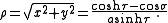
Again, a separable equation is obtained. A particular solution obtained by separation of variables
Separation of variables
In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....
is then:
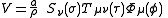
where each function is a linear combination of:
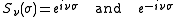
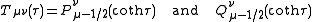
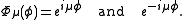
Note that although the toroidal harmonics are used again for the T function, the argument is
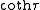 rather than
rather than 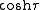 and the
and the 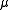 and
and  indices are exchanged. This method is useful for situations in which the boundary conditions are independent of the spherical angle
indices are exchanged. This method is useful for situations in which the boundary conditions are independent of the spherical angle 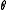 , such as the charged ring, an infinite half plane, or two parallel planes. For identities relating the toroidal harmonics with argument hyperbolic
, such as the charged ring, an infinite half plane, or two parallel planes. For identities relating the toroidal harmonics with argument hyperboliccosine with those of argument hyperbolic cotangent, see the Whipple formulae
Whipple formulae
In the theory of special functions, Whipple's transformation for Legendre functions, named after Francis John Welsh Whipple, arise from a general expression, concerning associated Legendre functions...
.

