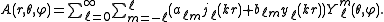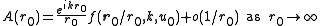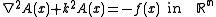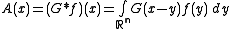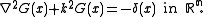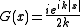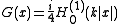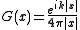Helmholtz equation
Encyclopedia
The Helmholtz equation, named for Hermann von Helmholtz
, is the elliptic partial differential equation
where ∇2 is the Laplacian
, k is the wavenumber
, and A is the amplitude
.
s (PDEs) in both space and time. The Helmholtz equation, which represents the time-independent form of the original equation, results from applying the technique of separation of variables
to reduce the complexity of the analysis.
For example, consider the wave equation
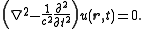
Separation of variables begins by assuming that the wave function u(r, t) is in fact separable:
Substituting this form into the wave equation, and then simplifying, we obtain the following equation: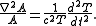
Notice the expression on the left-hand side depends only on r, whereas the right-hand expression depends only on t. As a result, this equation is valid in the general case if and only if both sides of the equation are equal to a constant value. From this observation, we obtain two equations, one for A(r), the other for T(t):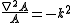
and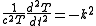
where we have chosen, without loss of generality, the expression −k2 for the value of the constant. (It is equally valid to use any constant k as the separation constant; −k2 is chosen only for convenience in the resulting solutions.)
Rearranging the first equation, we obtain the Helmholtz equation: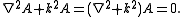
Likewise, after making the substitution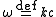
the second equation becomes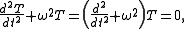
where k is the wave vector
and ω is the angular frequency
.
which corresponds to the time-harmonic solution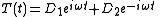
for arbitrary (complex-valued) constants C and D, which will depend on the initial conditions and boundary conditions, and subject to the dispersion relation
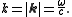
We now have Helmholtz's equation for the spatial variable r and a second-order ordinary differential equation
in time. The solution in time will be a linear combination
of sine
and cosine functions, with angular frequency
of ω, while the form of the solution in space will depend on the boundary conditions. Alternatively, integral transforms, such as the Laplace or Fourier transform
, are often used to transform a hyperbolic PDE
into a form of the Helmholtz equation.
Because of its relationship to the wave equation, the Helmholtz equation arises in problems in such areas of physics
as the study of electromagnetic radiation
, seismology
, and acoustics
.
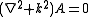
can be obtained using separation of variables
.
in 1829, the equilateral triangle by Gabriel Lamé
in 1852, and the circular membrane by Alfred Clebsch
in 1862. The elliptical drumhead was studied by Émile Mathieu
, leading to Mathieu's differential equation. The solvable shapes all correspond to shapes whose dynamical billiard table is integrable
, that is, not chaotic. When the motion on a correspondingly-shaped billiard table is chaotic, then no closed form solutions to the Helmholtz equation are known. The study of such systems is known as quantum chaos
, as the Helmholtz equation and similar equations occur in quantum mechanics
.
If the edges of a shape are straight line segments, then a solution is integrable or knowable in closed-form only if it is expressible as a finite linear combination of plane waves that satisfy the boundary conditions (zero at the boundary, i.e., membrane clamped).
An interesting situation happens with a shape where about half
of the solutions are integrable, but the remainder are not. A simple shape where this happens is with the regular hexagon. If the wavepacket describing a quantum billiard ball is made up of only the closed-form solutions, its motion will not be chaotic, but if any amount of non-closed-form solutions are included, the quantum billiard motion becomes chaotic. Another simple shape where this happens is with an "L" shape made by reflecting a square down, then to the right.
If the domain is a circle of radius a, then it is appropriate to introduce polar coordinates r and θ. The Helmholtz equation takes the form
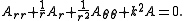
We may impose the boundary condition that A vanish if r=a; thus
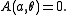
The method of separation of variables leads to trial solutions of the form
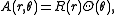
where Θ must be periodic of period 2π. This leads to
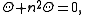
and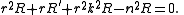
It follows from the periodicity condition that
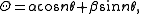
and that n must be an integer. The radial component R has the form
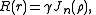
where the Bessel function
Jn(ρ) satisfies Bessel's equation
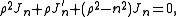
and ρ=kr. The radial function Jn
has infinitely many roots for each value of n, denoted by ρm,n. The boundary condition that A vanishes where r=a will be satisfied if the corresponding wavenumbers are given by
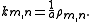
The general solution A then takes the form of a doubly infinite sum of terms involving products of
These solutions are the modes of vibration of a circular drumhead
.
This solution arises from the spatial solution of the wave equation
and diffusion equation. Here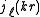
and 
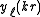are the spherical Bessel functions, and
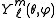
are the spherical harmonics
(Abramowitz and Stegun, 1964). Note that these forms are general solutions, and require boundary conditions to be specified to be used in any specific case. For infinite exterior domains, a radiation condition may also be required (Sommerfeld, 1949).
For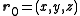
function 
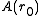has asymptotics
where function ƒ is called scattering amplitude and
is the value of A at each boundary point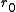 
.
where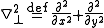
is the transverse part of the Laplacian
.
This equation has important applications in the science of optics
, where it provides solutions that describe the propagation of electromagnetic waves (light) in the form of either paraboloidal
waves or Gaussian beam
s. Most laser
s emit beams that take this form.
In the paraxial approximation
, the complex
magnitude
of the electric field
E becomes
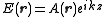
where A represents the complex-valued amplitude of the electric field, which modulates the sinusoidal plane wave represented by the exponential factor.
The paraxial approximation places certain upper limits on the variation of the amplitude function A with respect to longitudinal distance z. Specifically:
and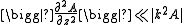
These conditions are equivalent to saying that the angle θ between the wave vector
k and the optical axis z must be small enough so that
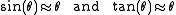
The paraxial form of the Helmholtz equation is found by substituting the above-stated complex magnitude of the electric field into the general form of the Helmholtz equation as follows.
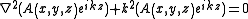
Expansion and cancellation yields the following:
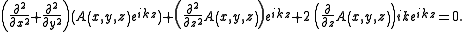
Because of the paraxial inequalities stated above, the ∂2A/∂z2 factor is neglected in comparison with the ∂A/∂z factor. The yields the Paraxial Helmholtz equation.
where ƒ : Rn → C is a given function with compact support, and n = 1, 2, 3. This equation is very similar to the screened Poisson equation
, and would be identical if the plus sign (in front of the k term) is switched to a minus sign.
In order to solve this equation uniquely, one needs to specify a boundary condition at infinity, which is typically the Sommerfeld radiation condition
uniformly in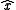
with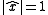 
, where the vertical bars denote the Euclidean norm.
With this condition, the solution to the inhomogeneous Helmholtz equation is the convolution
(notice this integral is actually over a finite region, since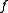
has compact support). Here, 
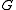is the Green's function
of this equation, that is, the solution to the inhomogeneous Helmholtz equation with ƒ equaling the Dirac delta function
, so G satisfies
The expression for the Green's function depends on the dimension
of the space. One has
for n = 1,
for n = 2, where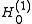
is a Hankel function, and
for n = 3. Note that we have chosen the boundary condition that the Green's function is an outgoing wave for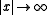
.
Hermann von Helmholtz
Hermann Ludwig Ferdinand von Helmholtz was a German physician and physicist who made significant contributions to several widely varied areas of modern science...
, is the elliptic partial differential equation
where ∇2 is the Laplacian
Laplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
, k is the wavenumber
Wavenumber
In the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector...
, and A is the amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
.
Motivation and uses
The Helmholtz equation often arises in the study of physical problems involving partial differential equationPartial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s (PDEs) in both space and time. The Helmholtz equation, which represents the time-independent form of the original equation, results from applying the technique of separation of variables
Separation of variables
In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....
to reduce the complexity of the analysis.
For example, consider the wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
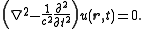
Separation of variables begins by assuming that the wave function u(r, t) is in fact separable:
Substituting this form into the wave equation, and then simplifying, we obtain the following equation:
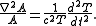
Notice the expression on the left-hand side depends only on r, whereas the right-hand expression depends only on t. As a result, this equation is valid in the general case if and only if both sides of the equation are equal to a constant value. From this observation, we obtain two equations, one for A(r), the other for T(t):
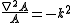
and
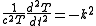
where we have chosen, without loss of generality, the expression −k2 for the value of the constant. (It is equally valid to use any constant k as the separation constant; −k2 is chosen only for convenience in the resulting solutions.)
Rearranging the first equation, we obtain the Helmholtz equation:
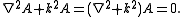
Likewise, after making the substitution
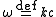
the second equation becomes
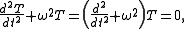
where k is the wave vector
Wave vector
In physics, a wave vector is a vector which helps describe a wave. Like any vector, it has a magnitude and direction, both of which are important: Its magnitude is either the wavenumber or angular wavenumber of the wave , and its direction is ordinarily the direction of wave propagation In...
and ω is the angular frequency
Angular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
.
Harmonic solutions
It is relatively easy to show that solutions to the Helmholtz equation will take the form:
which corresponds to the time-harmonic solution
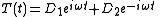
for arbitrary (complex-valued) constants C and D, which will depend on the initial conditions and boundary conditions, and subject to the dispersion relation
Dispersion relation
In physics and electrical engineering, dispersion most often refers to frequency-dependent effects in wave propagation. Note, however, that there are several other uses of the word "dispersion" in the physical sciences....
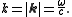
We now have Helmholtz's equation for the spatial variable r and a second-order ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
in time. The solution in time will be a linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of sine
Sine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
and cosine functions, with angular frequency
Angular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
of ω, while the form of the solution in space will depend on the boundary conditions. Alternatively, integral transforms, such as the Laplace or Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
, are often used to transform a hyperbolic PDE
Hyperbolic partial differential equation
In mathematics, a hyperbolic partial differential equation of order n is a partial differential equation that, roughly speaking, has a well-posed initial value problem for the first n−1 derivatives. More precisely, the Cauchy problem can be locally solved for arbitrary initial data along...
into a form of the Helmholtz equation.
Because of its relationship to the wave equation, the Helmholtz equation arises in problems in such areas of physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
as the study of electromagnetic radiation
Electromagnetic radiation
Electromagnetic radiation is a form of energy that exhibits wave-like behavior as it travels through space...
, seismology
Seismology
Seismology is the scientific study of earthquakes and the propagation of elastic waves through the Earth or through other planet-like bodies. The field also includes studies of earthquake effects, such as tsunamis as well as diverse seismic sources such as volcanic, tectonic, oceanic,...
, and acoustics
Acoustics
Acoustics is the interdisciplinary science that deals with the study of all mechanical waves in gases, liquids, and solids including vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician while someone working in the field of acoustics...
.
Solving the Helmholtz equation using separation of variables
The general solution to the spatial Helmholtz equation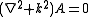can be obtained using separation of variables
Separation of variables
In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....
.
Vibrating membrane
The two-dimensional analogue of the vibrating string is the vibrating membrane, with the edges clamped to be motionless. The Helmholtz equation was solved for many basic shapes in the 19th century: the rectangular membrane by Siméon Denis PoissonSiméon Denis Poisson
Siméon Denis Poisson , was a French mathematician, geometer, and physicist. He however, was the final leading opponent of the wave theory of light as a member of the elite l'Académie française, but was proven wrong by Augustin-Jean Fresnel.-Biography:...
in 1829, the equilateral triangle by Gabriel Lamé
Gabriel Lamé
Gabriel Léon Jean Baptiste Lamé was a French mathematician.-Biography:Lamé was born in Tours, in today's département of Indre-et-Loire....
in 1852, and the circular membrane by Alfred Clebsch
Alfred Clebsch
Rudolf Friedrich Alfred Clebsch was a German mathematician who made important contributions to algebraic geometry and invariant theory. He attended the University of Königsberg and was habilitated at Berlin. He subsequently taught in Berlin and Karlsruhe...
in 1862. The elliptical drumhead was studied by Émile Mathieu
Émile Léonard Mathieu
Émile Léonard Mathieu was a French mathematician. He is most famous for his work in group theory and mathematical physics. He has given his name to the Mathieu functions, Mathieu groups and Mathieu transformation...
, leading to Mathieu's differential equation. The solvable shapes all correspond to shapes whose dynamical billiard table is integrable
Integrable system
In mathematics and physics, there are various distinct notions that are referred to under the name of integrable systems.In the general theory of differential systems, there is Frobenius integrability, which refers to overdetermined systems. In the classical theory of Hamiltonian dynamical...
, that is, not chaotic. When the motion on a correspondingly-shaped billiard table is chaotic, then no closed form solutions to the Helmholtz equation are known. The study of such systems is known as quantum chaos
Quantum chaos
Quantum chaos is a branch of physics which studies how chaotic classical dynamical systems can be described in terms of quantum theory. The primary question that quantum chaos seeks to answer is, "What is the relationship between quantum mechanics and classical chaos?" The correspondence principle...
, as the Helmholtz equation and similar equations occur in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
.
If the edges of a shape are straight line segments, then a solution is integrable or knowable in closed-form only if it is expressible as a finite linear combination of plane waves that satisfy the boundary conditions (zero at the boundary, i.e., membrane clamped).
An interesting situation happens with a shape where about half
of the solutions are integrable, but the remainder are not. A simple shape where this happens is with the regular hexagon. If the wavepacket describing a quantum billiard ball is made up of only the closed-form solutions, its motion will not be chaotic, but if any amount of non-closed-form solutions are included, the quantum billiard motion becomes chaotic. Another simple shape where this happens is with an "L" shape made by reflecting a square down, then to the right.
If the domain is a circle of radius a, then it is appropriate to introduce polar coordinates r and θ. The Helmholtz equation takes the form
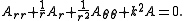
We may impose the boundary condition that A vanish if r=a; thus
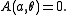
The method of separation of variables leads to trial solutions of the form
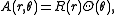
where Θ must be periodic of period 2π. This leads to
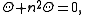
and
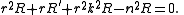
It follows from the periodicity condition that
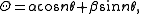
and that n must be an integer. The radial component R has the form
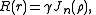
where the Bessel function
Bessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
Jn(ρ) satisfies Bessel's equation
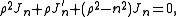
and ρ=kr. The radial function Jn
has infinitely many roots for each value of n, denoted by ρm,n. The boundary condition that A vanishes where r=a will be satisfied if the corresponding wavenumbers are given by
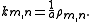
The general solution A then takes the form of a doubly infinite sum of terms involving products of
These solutions are the modes of vibration of a circular drumhead
Vibrations of a circular drum
The vibrations of an idealized circular drum, essentially an elastic membrane of uniform thickness attached to a rigid circular frame, are solutions of the wave equation with zero boundary conditions....
.
Three-dimensional solutions
In spherical coordinates, the solution is:
This solution arises from the spatial solution of the wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
and diffusion equation. Here
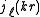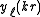and are the spherical Bessel functions, and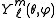are the spherical harmonics
Spherical harmonics
In mathematics, spherical harmonics are the angular portion of a set of solutions to Laplace's equation. Represented in a system of spherical coordinates, Laplace's spherical harmonics Y_\ell^m are a specific set of spherical harmonics that forms an orthogonal system, first introduced by Pierre...
(Abramowitz and Stegun, 1964). Note that these forms are general solutions, and require boundary conditions to be specified to be used in any specific case. For infinite exterior domains, a radiation condition may also be required (Sommerfeld, 1949).
For
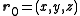function 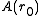has asymptotics
where function ƒ is called scattering amplitude and
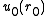is the value of A at each boundary point 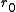.Paraxial approximation
The paraxial approximation of the Helmholtz equation is (ref: "Introduction to Fourier Optics", 2nd ed., J. W. Goodman, p61-62):where
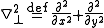is the transverse part of the LaplacianLaplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
.
This equation has important applications in the science of optics
Optics
Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
, where it provides solutions that describe the propagation of electromagnetic waves (light) in the form of either paraboloidal
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
waves or Gaussian beam
Gaussian beam
In optics, a Gaussian beam is a beam of electromagnetic radiation whose transverse electric field and intensity distributions are well approximated by Gaussian functions. Many lasers emit beams that approximate a Gaussian profile, in which case the laser is said to be operating on the fundamental...
s. Most laser
Laser
A laser is a device that emits light through a process of optical amplification based on the stimulated emission of photons. The term "laser" originated as an acronym for Light Amplification by Stimulated Emission of Radiation...
s emit beams that take this form.
In the paraxial approximation
Paraxial approximation
In geometric optics, the paraxial approximation is a small-angle approximation used in Gaussian optics and ray tracing of light through an optical system ....
, the complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
magnitude
Magnitude (mathematics)
The magnitude of an object in mathematics is its size: a property by which it can be compared as larger or smaller than other objects of the same kind; in technical terms, an ordering of the class of objects to which it belongs....
of the electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
E becomes
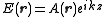
where A represents the complex-valued amplitude of the electric field, which modulates the sinusoidal plane wave represented by the exponential factor.
The paraxial approximation places certain upper limits on the variation of the amplitude function A with respect to longitudinal distance z. Specifically:
and
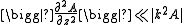
These conditions are equivalent to saying that the angle θ between the wave vector
Wave vector
In physics, a wave vector is a vector which helps describe a wave. Like any vector, it has a magnitude and direction, both of which are important: Its magnitude is either the wavenumber or angular wavenumber of the wave , and its direction is ordinarily the direction of wave propagation In...
k and the optical axis z must be small enough so that
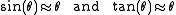
The paraxial form of the Helmholtz equation is found by substituting the above-stated complex magnitude of the electric field into the general form of the Helmholtz equation as follows.
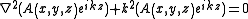
Expansion and cancellation yields the following:
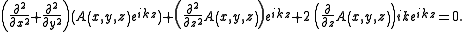
Because of the paraxial inequalities stated above, the ∂2A/∂z2 factor is neglected in comparison with the ∂A/∂z factor. The yields the Paraxial Helmholtz equation.
Inhomogeneous Helmholtz equation
The inhomogeneous Helmholtz equation is the equation
where ƒ : Rn → C is a given function with compact support, and n = 1, 2, 3. This equation is very similar to the screened Poisson equation
Screened Poisson equation
In Physics, the screened Poisson equation is the following partial differential equation:\left[ \Delta - \lambda^2 \right] u = - f...
, and would be identical if the plus sign (in front of the k term) is switched to a minus sign.
In order to solve this equation uniquely, one needs to specify a boundary condition at infinity, which is typically the Sommerfeld radiation condition
uniformly in
with , where the vertical bars denote the Euclidean norm.With this condition, the solution to the inhomogeneous Helmholtz equation is the convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
(notice this integral is actually over a finite region, since
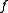has compact support). Here, 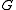is the Green's functionGreen's function
In mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
of this equation, that is, the solution to the inhomogeneous Helmholtz equation with ƒ equaling the Dirac delta function
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
, so G satisfies
The expression for the Green's function depends on the dimension
of the space. One has
for n = 1,
for n = 2, where
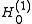is a Hankel function, and
for n = 3. Note that we have chosen the boundary condition that the Green's function is an outgoing wave for
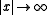.External links
- Helmholtz Equation at EqWorld: The World of Mathematical Equations.
- Vibrating Circular Membrane by Sam Blake, The Wolfram Demonstrations Project.